QUADRATIC ρ-FUNCTIONAL INEQUALITIES IN BANACH SPACES∗

Research Institute for Natural Sciences,Hanyang University,Seoul 133-791,Republic of Korea

E-mail:baak@hanyang.ac.kr

QUADRATIC ρ-FUNCTIONAL INEQUALITIES IN BANACH SPACES∗

Choonkil PARK

Research Institute for Natural Sciences,Hanyang University,Seoul 133-791,Republic of Korea

E-mail:baak@hanyang.ac.kr

In this paper,we solve the quadratic ρ-functional inequalities

where ρ is a fxed complex number with|ρ|＜1,and

Hyers-Ulam stability;quadratic ρ-functional equation;quadratic ρ-functional inequality;complex Banach space

2010 MR Subject Classifcation39B62;39B52

1 Introduction and Preliminaries

The stability problem of functional equations originated from a question of Ulam[15]concerning the stability of group homomorphisms.

The functional equation

is called the Cauchy equation.In particular,every solution of the Cauchy equation is said to be an additive mapping.Hyers[10]gave a frst afrmative partial answer to the question of Ulam for Banach spaces.Hyers’Theorem was generalized by Aoki[1]for additive mappings and by Rassias[12]for linear mappings by considering an unbounded Cauchy diference.Ageneralization of the Rassias theorem was obtained by G˘avruta[7]by replacing the unbounded Cauchy diference by a general control function in the spirit of Rassias’approach.

The functional equation

is called the quadratic functional equation.In particular,every solution of the quadratic functional equation is said to be a quadratic mapping.The stability of quadratic functional equation was proved by Skof[14]for mappings f:E1→E2,where E1is a normed space and E2is a Banach space.Cholewa[4]noticed that the theorem of Skof is still true if the relevant domain E1is replaced by an Abelian group.

The functional equation

is called a Jensen type quadratic equation.See[2,3,5]for more information on functional equations and their stability.

In[8],Gil´anyi showed that if f satisfes the functional inequality

then f satisfes the Jordan-von Neumann functional equation

See also[13].Gil´anyi[9]and Fechner[6]proved the Hyers-Ulam stability of the functional inequality(1.1).Park,Cho and Han[11]proved the Hyers-Ulam stability of additive functional inequalities.

In Section 2,we solve the quadratic ρ-functional inequality(0.1)and prove the Hyers-Ulam stability of the quadratic ρ-functional inequality(0.1)in complex Banach spaces.We moreover prove the Hyers-Ulam stability of a quadratic ρ-functional equation associated with the quadratic ρ-functional inequality(0.1)in complex Banach spaces.

In Section 3,we solve the quadratic ρ-functional inequality(0.2)and prove the Hyers-Ulam stability of the quadratic ρ-functional inequality(0.2)in complex Banach spaces.We moreover prove the Hyers-Ulam stability of a quadratic ρ-functional equation associated with the quadratic ρ-functional inequality(0.2)in complex Banach spaces.

Throughout this paper,assume that X is a complex normed space and that Y is a complex Banach space.

2 Quadratic ρ-Functional Inequality(0.1)

Throughout this section,assume that ρ is a fxed complex number with|ρ|＜1.

In this section,we solve and investigate the quadratic ρ-functional inequality(0.1)in complex normed spaces.

Lemma 2.1A mapping f:X→Y satisfesfor all x,y∈X if and only if f:X→Y is quadratic.

ProofAssume that f:X→Y satisfes(2.1).

Letting x=y=0 in(2.1),we get‖2f(0)‖≤|ρ|‖2f(0)‖.So f(0)=0.

Letting y=x in(2.1),we get‖f(2x)-4f(x)‖≤0 and so f(2x)=4f(x)for all x∈X.

Thus

for all x∈X.

It follows from(2.1)and(2.2)that

and so

for all x,y∈X.

The convesre is obviously true.

Corollary 2.2A mapping f:X→Y satisfes

for all x,y∈X if and only if f:X→Y is quadratic.

The functional equation(2.3)is called a quadratic ρ-functional equation.

We prove the Hyers-Ulam stability of the quadratic ρ-functional inequality(2.1)in complex Banach spaces.

Theorem 2.3Let φ:X2→[0,∞)be a function and let f:X→Y be a mapping such that

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

ProofLetting x=y=0 in(2.5),we get‖2f(0)‖≤|ρ|‖2f(0)‖.So f(0)=0.

Letting y=x in(2.5),we get

for all x∈X.So

for all x∈X.Hence

for all x∈X.Moreover,letting l=0 and passing the limit m→∞in(2.8),we get(2.6).

It follows from(2.4)and(2.5)that

for all x,y∈X.So

for all x,y∈X.By Lemma 2.1,the mapping h:X→Y is quadratic.

Now,let T:X→Y be another quadratic mapping satisfying(2.6).Then we have

which tends to zero as q→∞for all x∈X.So we can conclude that h(x)=T(x)for all x∈X.This proves the uniqueness of h.Thus the mapping h:X→Y is a unique quadratic mapping satisfying(2.6).

Corollary 2.4Let r＞2 and θ be nonnegative real numbers,and let f:X→Y be a mapping such that

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

Theorem 2.5Let φ:X2→[0,∞)be a function with φ(0,0)=0 and let f:X→Y be a mapping satisfying(2.5)and

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

ProofIt follows from(2.7)that

for all x∈X.Hence

for all x∈X.Moreover,letting l=0 and passing the limit m→∞in(2.13),we get(2.12). The rest of the proof is similar to the proof of Theorem 2.3.?Corollary 2.6Let r＜2 and θ be positive real numbers,and let f:X→Y be a mapping satisfying(2.9).Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

By the triangle inequality,we have

As corollaries of Theorems 2.3 and 2.5,we obtain the Hyers-Ulam stability results for the quadratic ρ-functional equation(2.3)in complex Banach spaces.

Corollary 2.7Let φ:X2→[0,∞)be a function and let f:X→Y be a mapping satisfying(2.4)and

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y satisfying(2.6).

Corollary 2.8Let r＞2 and θ be nonnegative real numbers,and let f:X→Y be a mapping such that

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y satisfying(2.10).

Corollary 2.9Let φ:X2→[0,∞)be a function with φ(0,0)=0 and let f:X→Y be a mapping satisfying(2.11)and(2.15).Then there exists a unique quadratic mapping h:X→Y satisfying(2.12).

Corollary 2.10Let r＜2 and θ be positive real numbers,and let f:X→Y be a mapping satisfying(2.16).Then there exists a unique quadratic mapping h:X→Y satisfying (2.14).

Remark 2.11If ρ is a real number such that-1＜ρ＜1 and Y is a real Banach space, then all the assertions in this section remain valid.

3 Quadratic ρ-Functional Inequality(0.2)

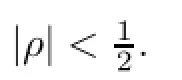
In this section,we solve and investigate the quadratic ρ-functional inequality(0.2)in complex normed spaces.

Lemma 3.1A mapping f:X→Y satisfes

for all x,y∈X if and only if f:X→Y is quadratic.

ProofAssume that f:X→Y satisfes(3.1).

Letting x=y=0 in(3.1),we get‖2f(0)‖≤|ρ|‖2f(0)‖.So f(0)=0.

Letting y=0 in(3.1),we get

It follows from(3.1)and(3.2)that

and so

for all x,y∈X.

The converse is obviously true.

for all x,y∈X and only if f:X→Y is quadratic.

The functional equation(3.3)is called a quadratic ρ-functional equation.

We prove the Hyers-Ulam stability of the quadratic ρ-functional inequality(3.1)in complex Banach spaces.

Theorem 3.3Let φ:X2→[0,∞)be a function and let f:X→Y be a mapping satisfying

Corollary 3.2A mapping f:X→Y satisfes

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

ProofLetting x=y=0 in(3.5),we get‖2f(0)‖≤|ρ|‖2f(0)‖.So f(0)=0.

Letting y=0 in(3.5),we get

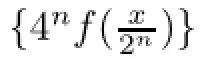
for all x∈X.Moreover,letting l=0 and passing the limit m→∞in(3.8),we get(3.6).

The rest of the proof is similar to the proof of Theorem 2.3.?

Corollary 3.4Let r＞2 and θ be nonnegative real numbers,and let f:X→Y be a mapping such that

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

Theorem 3.5Let φ:X2→[0,∞)be a function with φ(0,0)=0 and let f:X→Y be a mapping satisfying(3.5)and

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

ProofIt follows from(3.7)that

for all x∈X.Hence

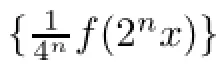
for all x∈X.Moreover,letting l=0 and passing the limit m→∞in(3.13),we get(3.12).

The rest of the proof is similar to the proof of Theorems 2.3.?

Corollary 3.6Let r＜2 and θ be nonnegative real numbers,and let f:X→Y be a mapping satisfying(3.9).Then there exists a unique quadratic mapping h:X→Y such that

for all x∈X.

By the triangle inequality,we have

As corollaries of Theorems 3.3 and 3.5,we obtain the Hyers-Ulam stability results for the quadratic ρ-functional equation(3.3)in complex Banach spaces.

Corollary 3.7Let φ:X2→[0,∞)be a function and let f:X→Y be a mapping satisfying(3.4)and

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y satisfying(3.6).

Corollary 3.8Let r＞2 and θ be nonnegative real numbers,and let f:X→Y be a mapping such that

for all x,y∈X.Then there exists a unique quadratic mapping h:X→Y satisfying(3.10).

Corollary 3.9Let φ:X2→[0,∞)be a function with φ(0,0)=0 and let f:X→Y be a mapping satisfying(3.11)and(3.15).Then there exists a unique quadratic mapping h:X→Y satisfying(3.12).

Corollary 3.10Let r＜2 and θ be positive real numbers,and let f:X→Y be a mapping satisfying(3.16).Then there exists a unique quadratic mapping h:X→Y satisfying (3.14).

[1]Aoki T.On the stability of the linear transformation in Banach spaces.J Math Soc Japan,1950,2:64-66

[2]Azadi Kenary H.Random approximation of an additive functional equation of m-Appollonius type.Acta Math Sci,2012,32B:1813-1825

[3]Azadi Kenary H.Approximation of a Cauchy-Jensen functional equation in non-Archimedean normed spaces.Acta Math Sci,2012,32B:2247-2258

[4]Cholewa P W.Remarks on the stability of functional equations.Aequationes Math,1984,27:76-86

[5]Ebadian A,Nikoufar I,Rassias Th M,Ghobadipour N.Stability of generalized derivations on Hilbert C∗-modules associated with a Pexiderized Cauchy-Jensen type functional equation.Acta Math Sci,2012,32B: 1226-1238

[6]Fechner W.Stability of a functional inequalities associated with the Jordan-von Neumann functional equation.Aequationes Math,2006,71:149-161

[7]Gˇavruta P.A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings.J Math Anal Appl,1994,184:431-43

[8]Gil´anyi A.Eine zur Parallelogrammgleichung¨aquivalente Ungleichung.Aequationes Math,2001,62:303-309

[9]Gil´anyi A.On a problem by K Nikodem.Math Inequal Appl,2002,5:707-710

[10]Hyers D H.On the stability of the linear functional equation.Proc Natl Acad Sci,1941,27:222-224

[11]Park C,Cho Y,Han M.Functional inequalities associated with Jordan-von Neumann-type additive functional equations.J Inequal Appl,2007,2007:Article ID 41820

[12]Rassias Th M.On the stability of the linear mapping in Banach spaces.Proc Amer Math Soc,1978,72: 297-300

[13]R¨atz J.On inequalities associated with the Jordan-von Neumann functional equation.Aequationes Math, 2003,66:191-200

[14]Skof F.Propriet locali e approssimazione di operatori.Rend Sem Mat Fis Milano,1983,53:113-129

[15]Ulam S M.A Collection of the Mathematical Problems.New York:Interscience Publ,1960

∗Received April 30,2014.This work was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education,Science and Technology(NRF-2012R1A1A2004299).