BLOWING UP AND MULTIPLICITY OF SOLUTIONS FOR A FOURTH-ORDER EQUATION WITH CRITICAL NONLINEARITY∗

Department of mathematics,University of Monastir,Tunisia

E-mail:siwar ammar84@yahoo.fr

Mokhles HAMMAMI

Department of mathematics,Faculty of Sciences of sfax,University of Sfax,Tunisia

E-mail:Mokhless.Hammami@fss.rnu.tn

BLOWING UP AND MULTIPLICITY OF SOLUTIONS FOR A FOURTH-ORDER EQUATION WITH CRITICAL NONLINEARITY∗

Siwar AMMAR

Department of mathematics,University of Monastir,Tunisia

E-mail:siwar ammar84@yahoo.fr

Mokhles HAMMAMI

Department of mathematics,Faculty of Sciences of sfax,University of Sfax,Tunisia

E-mail:Mokhless.Hammami@fss.rnu.tn

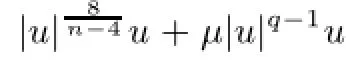
fourth order elliptic equations;critical Sobolev exponent;blow up solution

2010 MR Subject Classifcation35J20;35J60

1 Introduction and Statement of Results

This paper concerns the concentration phenomena for the following nonlinear equation under the Navier boundary conditions,

The motivation for investigating(Pµ)comes from its resemblence some geometric equations involving Paneitz operator(see for instance[6,13,17]).

In the last decades,there have been many works in the study of concentration phenomena for second order elliptic equation with critical Sobolev exponent;see for example[1,4,7,11,12,15,16,21,25-31]and the references therein.In sharp contrast to this,very little is known for fourth order elliptic equations.

Existence and multiplicity of solutions of(Pµ)have been studied intensively by many authors with the exponents p and q.In[33],Van Der Vorst proved that if q∈[1,p[andµ≤0 then(Pµ)has no solution in starshaped domains Ω⊂Rn,whereas Ebobisse and Ould Ahmedou proved in[18]that(P0)has a solution provided that some homology group of Ω is nontrivial in the sense Hk(Ω,Z2)/=0 for some integer k.Nevertheless,Gazzola,Grunau and Squassina[19] gave the example of contractible domains on which a solution still exists,showing that both topology and geometry of the domains play a role.

In case n≥8 and 1≤q＜p or n=5,6,7 and(12-n)/(n-4)＜q＜(n+4)/(n-4),Melo and Santos[24],proved that if Ω has a rich topology,described by its Lusternik-Schnirelmann category,then multiple solutions to problem(Pµ)exist providedµ＞0 is sufciently small.The approach used on[24]is diferent to our method.It is based on some analysis on the Nehari manifold associated with the problem(Pµ).

Note that,the most results are concerning the large dimensions.The purpose of the present paper is to study solutions for(Pµ)for the critical dimensions n=5,6,7 and q∈]4/(n-4),(12-n)/(n-4)[.More precisely,for all positive solutions which concentrate around two points of Ω,we prove that the concentration speeds are of the same order and the distance of the concentration points from each other and from the boundary are bounded.We will also establish the existence of positive solution which concentrate at two points of Ω,where Ω=(Ωa)ais a smooth ringshaped open set and we will prove if Ω has a rich topology,described by its Lusternik-Schnirelmann category,then multiple solutions to problem(Pµ)exist provided µ＞0 large enough.We note that the choose of the variableµ(in Theorem 1.4)depends on the remainder termµ-(n-4)(q+1)/(12-n-(n-4)q)which appears in our expansions(see section 5, equation(5.4)).In fact,since we assume that q＜(12-n)/(n-4),thenµhas to be large enough to obtain that the previous term is small enough with respect to the principal terms in our expansions.Furthermore,this remainder term gives us an idea on the choose of[24](since in their case q＞(12-n)/(n-4)and thenµhas to be small enough).In Theorem 1.2,the remainder term which appears in Proposition 4.4 is ρ(X)(n-4)(q-2)/(12-n-(n-4)q),where ρ(X)is the frst eigenvalue of the Matrix M(X)defned in(1.4),since we assume that q＜(12-n)/(n-4) to obtain that the previous term is small enough with respect to the principal terms in our expansions.

We remarque that our method works also to prove the result of[24].The proof of our resultsis inspired by Rey[28].Compared with the second-order case,further technical problems arise which are overcome by careful and delicate expansions of the Euler functional associated to (Pµ)and its gradient near a neighborhood of highly concentrated functions.In fact,in our case we cannot use,as in the laplacien case,the method of moving planes in order to show that the distances of the blow up points from each other and from the boundary of the domain are bounded.This is due to the fact that the Navier boundary condition is not invariant under the Kelvin transformation of the biharmonic operator.To overcome this difculty,we use the techniques developed by Bahri[2]and Rey[29]in the framework of the theory of critical points at infnity.

To state our results,we need to introduce some notations.We denote by G the Green’s function of Δ2,that is,for all x∈Ω:

where δxdenotes the Dirac mass at x and c=(n-4)(n-2)|Sn-1|.We also denote by H the regular part of G,that is,

and H satisfes

For λ＞0 and x∈Rn,let

It is well known(see[22])that δ(x,λ)are the only solutions of

They are also the only minimizers of the Sobolev inequality on the whole space,that is

The frst part of this paper is devoted to study the solution which concentrate around two points of Ω

2.d(xi,∂Ω)≥d0,for i=1,2.

3.|x1-x2|≥d0.

To state the existence result,we need to introduce some notations.

For X=(x1,x2)∈Ω2Γ,with Γ={(y,y),y∈Ω},we denote by M(X)the matrix defned by

Let ρ(X)be the least eigenvalue of M(X)and r(X)the eigenvector corresponding to ρ(X) whose norm is 1 and whose components are all strictly positive(see Appendix A of[4]).

We denote by Ω=(Ωa)a＞0is a ringshaped open sets in Rn.More precisely,let f be any smooth function

which is periodic of period π with respect to the θ1,.,.,θn-2and of period 2π with respect to θn-1.We set

where(r,θ1,···,θn-1)are the polar coordinates of x.

For each f we obtain an increasing family of smooth ringshaped open sets.In the following, Ha,Ga,ρadenote the functions H,G,ρ defned on Ωa×Ωa.

where the xikdenote here the k-th component of xi.

where η0,λ0,d0,k0are some suitable positive constants.

Now we state the result.

Theorem 1.2Let n=5,6 and assume thatµ＞0(resp.µ＜0).There exist(a0,a1)∈R2,0＜a1＜a0(resp 0＜a0＜a1)such that for any a∈[a1,a0[(resp.a∈]a0,a1]),there exists uaa solution of(Pµ)in Ωa,such that

where v∈EΛ,X,(A,Λ,X,v)∈M and 0＜ρ(X)＜ρ0(resp.ρ0＜ρ(X)＜0).

Concerning the sign-changing solution,we prove that(Pµ)has no sign-changing solutions which blows up at tow points.More precisely,we have

Theorem 1.3Let Ω be any smooth bounded domain in Rn,n∈{5,6,7}and let A be a fxed positive constant.For each|µ|≤A,the problem(Pµ)has no sign-changing solutions uµwhich satisfes

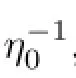
Next,we want to state a multiplicity result for problem(Pµ).For this purpose,we say that the category of F⊂Ω is k,denoted Cat(F,Ω),if F may be covered by k closed sets in Ω,each one contractible in Ω,but not by(k-1)such sets.We call category of Ω the positive integer Cat(Ω,Ω)(see[14]).

Theorem 1.4Let n=5,6 and Ω be any smooth and bounded domain in Rnof Ljusternik-Schnirelmann category k and let q∈]4/(n-4),(12-n)/(n-4)[.Forµ＞0,large enough,there are at least k+1 positive solutions of(Pµ).

Remark 1.5The dimension n=7 is excluded from Theorems 1.2 and 1.4.The reason is that in some expansions it appears(q-2)on some powers which we need to be positive(see Proposition 4.4).However,for n=7 the variable q∈]4/3,5/3[and this prove(q-2)becomes negative in the case n=7.

The remainder of the present paper is organized as follows.In the next,we prove Theorems 1.1 and 1.3.In Section 3,we develop the expansion of the functional associated to(Pµ)and its gradient,needed in the proof of Theorems 1.2 and 1.4.Section 4,is devoted to the proof of Theorem 1.2,while Theorem 1.4 is proved in Section 5.Lastly,we give in Appendix some useful estimates.

2 Proof of Theorems 1.1 and 1.3

This Section is devoted to the proof of Theorems 1.1 and 1.3.We will us some ideas introduced by Bahri[2]and some technical estimates.

We assume that there exists solution uµof(Pµ)as in(1.3)and(1.6).Arguing as in[2,3] and[29],we see that,there is a unique way to choose αi,xi,λiand v such that

where v∈EΛ,X.

In order to simplify the notations,in the remainder we write δi,Pδiand u instead of δ(xi,λi), Pδ(xi,λi)and uµ.

As usual in these types of problems,we frst deal with the v-part of u,in order to show that it is negligible with respect to the concentration phenomenon.Namely,we have the following estimate.

Lemma 2.1The function v defned in(2.1),satisfes the following estimate

where di:=d(xi,∂Ω)for i=1,2.

ProofSince u=α1Pδ1+γα2Pδ2+v is a solution of(Pµ)and v∈EΛ,X.Multiplying (Pµ)by v and integrating on Ω,we obtain

Hence,we have

where

According to[3]and[6],there exists a positive constant c such that

Using the Holder’s inequality and the Sobolev embedding theorem,we fnd

On another hand,for any v∈EΛ,X,we have

Now,we are able to obtain the following result which is a crucial point in the proof of our Theorems.

Proposition 2.2Assume that,u=α1Pδ1+γα2Pδ2+v is a solution of(Pµ).We have the following estimate:

ProofIt sufces to prove the proposition for i=1.Multiplying(Pµ)by Pδ1and integrating on Ω,we obtain

By Lemma 2.1,we write

Proof of Theorem 1.3Arguing by contradiction,let us suppose that the problem (Pµ)has a solution u as stated in Theorem 1.3.This solution has to satisfy(2.1),and from Proposition 2.2,we have

where i=1,2.

Without loss of generality,we can assume that λ2≥λ1.We distinguish two cases and we will prove that they cannot occur.This implies our theorem.

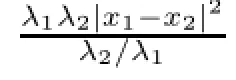
which implies that

Then from(2.10)and(2.12),we get

Using the fact that

which gives a contradiction.Hence this case cannot occur.

Now,using the fact that λ2≥λ1,an easy computation shows that

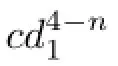
Using(2.13),(2.14)and(2.15)we have

Then we derive a contradiction and therefore this case cannot occur.Hence Theorem 1.3 is proved.?

Proof of Theorem 1.1Let us assume that problem(Pµ)has a solution u as stated in Theorem 1.1.We will proceed to proof the result in four steps:

The proof will be by contradiction.Assume that d1/d2→0.In this case,we have

Using Proposition 2.2,we derive

We deduce from(2.16)and(2.17)that

a contradiction.In the same way,we prove that d2/d1/→0.Hence the proof of Claim 1 is completed.

Assume that λ1/λ2→0.By Claim 1,we have(λ2d2)-1=o((λ1d1)-1).

Using the fact that λ1≤λ2,we have

By Proposition 2.2,we have

Using Claim 1 and(2.19),we derive

Hence,by(2.20)and Proposition 2.2,we obtain

We deduce that

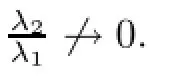
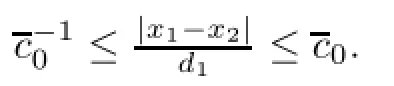
Two cases may occur.

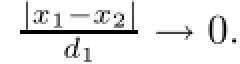
Using Proposition 2.2,we obtain

which gives a contradiction in this case.

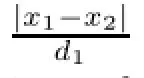
a contradiction.

Claim 4There exist a constant d0such that di=d(xi,∂Ω)≥d0,for i=1,2.

By Claims 1,2 and 3,we know that λ1and λ2are of the same order,|x1-x2|,d1and d2are of the same order.Assume that d1→0 and d1≤d2.Let νibe the outward normal vector at xi.Since d1,d2and|x1-x2|are of the same order,we have(see[4]and[8])

By Proposition 2.2,

then(2.22)implies

Then the Theorem follows for n∈{6,7}.In this case n=5,regarding the estimate of‖v‖,it is of the same order as the principle part of Proposition 2.2.We use an idea due to Rey[32], we have a better estimates of the integrals involving v,namely we write

where Bi=B(xi,di/4).

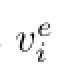
The estimate of Claim 3 in Proposition 2.2,becomes

Therefore the proof of the theorem follows in this case.

3 Expansion of the Functional and Its Gradient

If u is a positive critical point of J,u satisfes on Ω the problem(Pµ).Conversely,we see that any solution of(Pµ)is a critical point of J.

Let us defne the functional

where M is defned in(1.5).

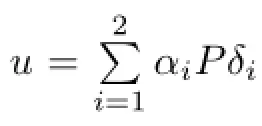
As usual in this types of problems,we frst deal with the v-part of u,in order to show that is negligible with respect to the concentration phenomenon.Namely,we prove the following.

Moreover,there exists(Bi,Ci,Di)∈R2×R2×(R2)nsuch that

where the xikis the k-th component of xi.

ProofK has been defned in(3.2),we write

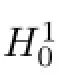
Now,we will estimate‖f(A,Λ,X)‖.

Then using the Holder’s inequality,and the fact that n＜12,we have

According to[3]and[6],there exists a positive constant c such that

Next,we prove a useful expansion of the derivative of the function K associated to(3.2), with respect to αi,λi,xi.

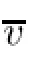
ProofTo prove Claim 1,using(2.6),(3.3)and(3.9),we write

Now,using the fact that,for k/=j

From(3.14),(3.15),Lemma A.1 and Proposition 3.1,Claim 1 follows.

Now,we prove Claim 2.As in Claim 1 we have

Using the fact that|xi-xj|＞d0,then

The Claim 2 follows from(3.14),(3.15),(3.16),(3.17),Lemma A.2 and Proposition 3.1.

Regarding Claim 3,its proof is similar to Claim 2,so we will omit it.?

Lemma 3.3Assume that(A,Λ,X,0)∈M,then the following expansion holds

ProofK has been defned in(3.2),we have

Now,using Lemma A.1,this lemma follows.

Now,setting

Proposition 3.4The coefcients Bi,Ciand Dikwhich occur in Proposition 3.1 satisfy the estimates

The left side is given by

By Proposition 3.2,we have

The solution of the system in Bi,Ci,Dikshows the result.?

4 Proof of Theorem 1.2

In Section 3,we minimizes the functional K with respect to v∈EΛ,X.

Let M1={(A,Λ,X)such that(A,Λ,X,0)∈M}.Our aim in this section is to optimize the C2-map

with respect to A=(α1,α2)and Λ=(λ1,λ2),i.e.,to fnd,for given X,AXand ΛXsuch that

For X∈Ω2Γ the matrix M(X)have two eigenvalues ρ(X)＜ρ′(X)corresponding respectively to the eigenvectors r(X)=(r1,r2)and r′(X)=(-r2,r1)(see[4]).One can choose r1and r2such that

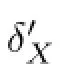
Setting

We prove the following result

Proposition 4.1Assume thatµ＞0.For each d0＞0 there exist ρ0＞0 and a C1-map

(i)(S)is satisfed with(A,Λ,X)=(AX,ΛX,X),

(ii)

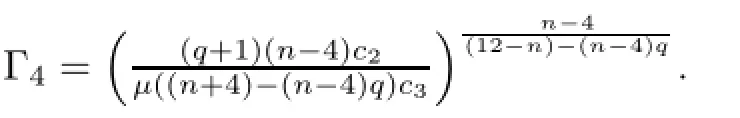
ProofFor X∈M2,we fnd AXand ΛXsuch that

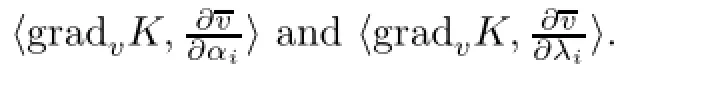
Taking the derivatives with respect to αiof the equalities

Using Proposition 3.1,therefore

On another hand,we write

In order to estimate ξik,ζikand θikl,we take the scalar product of(4.5)with Pδk,λk∂Pδk/∂λkand(λk)-1∂Pδk/∂xkl.On the left side,using the derivative with respect to λiof the equalities (4.3),we obtain

Therefore

We have also,

On the right side we use again(4.6),(4.8),(4.9),(3.21),(3.22),(3.23),(3.24)and from the linear system that we obtain,we derive

We fnd

Let us treat now the terms∂K/∂αiand∂K/∂λi.Observe that δ′=o(δ)and δ～‖Λ‖as ρ→0.

With the notation(3.19),(4.1)from Proposition 3.2,we derive

In the same way we prove that

Then,from(4.1)and(4.2),we derive

We have also,

Then,we set

with∈,∈′→0.With these notations,taking account of(4.4),(4.11),(4.12),(4.13),(4.14), (4.15),(4.16),(4.17)then(S1)may be written under the form

Where V′s and W′s are C1-functions which satisfy

Proposition 4.2The points(AX,ΛX)which occurs in Proposition 4.1 is a non degenerate critical point of the map w.

ProofNow,we will proof that the point(AX,ΛX)is a non-degenerate critical point of the map w.

Then we need to prove that the determinant Δ of the matrix is nonzero for(A,Λ)=(AX,ΛX).

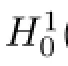
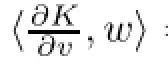
We have

On the other hand,we have

Replacing(4.25),(4.26),(4.27),(4.28)and(4.29)in equality(4.24),we obtain

Finally,we have

Thus,using(4.5),(4.10),(3.21),(3.22),(3.23),(3.24)and(4.31),we fnd

In the same way we prove that

We derive(4.23)with respect to αi,we obtain

and

Lastly,let us write

with wij∈EΛ,X.

On the left side we fnd

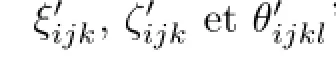
We deduce fnally that

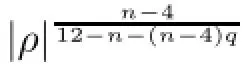
Coming back to(C2),the terms that we still have to estimate is the second derivatives of K with respect to αi’s and λi’s.The computations give us

where δijis the Kronecker symbol.

Then,equations(4.36)-(4.39)become,for(A,Λ)=(AX,ΛX)

Then we can compute the determinant△and we obtain

hence the result follows.

Now,we consider the following map defned by

where

ρ0being small enough in function of d0.

To complete the proof of this theorem we need to optimize K with respect to X.Each critical point X∈M2of K provides us with a critical point of J,hence a solution of(Pµ)if the function

is positive.In order to fnd such a critical point,we are going to use a min-max method based upon the special shape and properties of the domains Ωa.We will need the following Proposition.

Proposition 4.3We have the following expansions

ProofUsing Proposition 3.1,Lemma 3.3 and the fact that η=(η1,η2)=(α1-1,α2-1), we have

From(4.1)and Proposition 4.1,we derive

We get fnally

Hence,Proposition 4.3 follows.

Proposition 4.4We have the following expansions

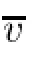
Using(2.19),we obtain

On another hand,(2.20)becomes

Using the Holder’s inequality and the Sobolev embedding theorem,we obtain

So that fnally,

Note that,we have

where

On another hand,diferentiating ρ with respect to x1k,we fnd

Thus,we see that

and we have the same expression for∂ρ/∂x2kintroverting the indices.Then,taking account of (4.1),we can write

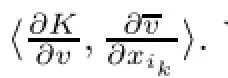
We have also,

Since

On the right hand side we use(3.21),(3.22),(3.23)and(3.24)and solving a linear system wefnd

From(3.4)we derive

Note that for(A,Λ)=(AX,ΛX),we have

so that,using(3.21),(3.22),(3.23),(3.24)to solve the linear system that we obtain by taking the scalar product of(3.4)with Pδi,∂K/∂λi,and(λi)-1∂K/∂xik,we get

Then,using again(3.21),(3.22),(3.23)and(3.24),we obtain the result.?

Thus,setting

where c is a positive constant.

We denote by σathe embedding

Finally,we set

Let us frst state some results about m.We already know that

m has also the following properties:

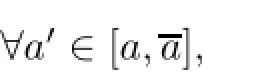
ii)if m(a)＜c,then m is continuous at a,

The proof of this proposition is done in page 836 of[28].

We need the following lemma to proof that the vector feld-gradKais pointing inward Ωa×Ωa.

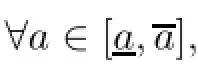
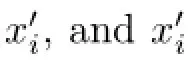
we have also,Ga(x1,x2)＞0 et∂Ga/∂x1k(x1,x2)ν1＜0,

Thus,the lemma follows.

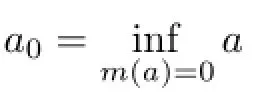
ProofWe start by proving that for a∈]a∗,a0[close enough to a0and ε＞0,Kahas a critical point between the levels m(a)-ε and m(a)+ε.Without loss of generality we may assume that ε＜m(a).We deduce from the defnition of Kaand Proposition 4.3 that

implies 0＜ρa(X)≤ρ0.

Therefore,if Kahas no critical value in[m(a)-ε,m(a)+ε],it is possible,using the fow

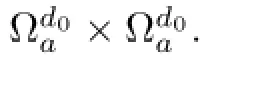
in contradiction with the defnition of m(a).

This ends the proof.

Since,by construction,(AXa,ΛXa,Xa,v)is a critical point of the functional Ka,ua∈H10(Ωa)∩H2(Ωa)defned by

with AXa=(α1,α2),ΛXa=(λ1,λ2),Xa=(x1,x2),et v=va=v(AXa,ΛXa,Xa),uais a critical point of the functional J,i.e.,a solution of the equation

5 Proof of Theorem 1.4

In this last section,Ω is any smooth and bounded domain in Rn,n=5,6 and our aim is to show that forµlarge enough,Problem(Pµ)has multiple solutions,in connection with the category of Ω.

We use the same method as in sections 3 and 4,with only one concentration point instead of two.We suppose,a priori,that x∈Ωd={x∈Ω/d(x,∂Ω)＞d},where d is a positive constant.

Step 1Optimization with respect to v.

Then,with a suitable choice of the positive constants η0,λ0,v0,(i.e,η0and v0,small enough, λ0large enough),we have

Moreover,there exists(B,C,D)∈R×R×(R)nsuch that

where the xkis the k-th component of x.

The proof is exactly the same as the proof of Proposition 3.1.The fact thatµis assumed to be variable and large makes the condition(5.2)necessary to prove that the quadratic form Qα,λ,xis coercive on Eλ,x.

As in Proposition 3.4,the variables B,C and D satisfy the following estimates

Step 2Optimization with respect to α and λ.

Now we have to fnd,x∈Ωdbeing fxed,αxand λxsuch that

We have

If we set

where∈is assumed to be small,(5.3)is satisfed forµlarge enough,and system(S1)turns out to be equivalent to

V and W are C1-functions which satisfy

Then,similarly to the results of Proposition 4.1,we obtain the following proposition

Proposition 5.2There exists a C1-map which to each x∈Ωdassociates(αx,λx)such that

(i)(S1)is satisfed

(ii)

Step 3Optimization with respect to x.

This is the last step.We fnd

on Ωd.

We see that for d small enough,and then forµlarge enough,there exists cd,µsuch that the level set

satisfes

Then,applying the Ljusternik-Schnirelmann theory to the function K defned on Kc,we obtain, since the gradient of-K is pointing inward on the boundary of Kc,then K has at least as many critical points in Ωdas the category of Kc.Moreover

for d small enough,since Ω is assumed to be smooth.Thus there exist at least k=cat(Ω) distinct points x1,···,xkof Ω such that K′(xi)=0.As a consequence,the functions

are solutions of(Pµ).

[1]Atkinson F V,Peletier L A.Elliptic equations with near critical growth.J DifEqu,1987,70:349-365

[2]Bahri A.Critical Point at Infnity in Some Variational Problems.Pitman Res Notes Math,Ser 182.Harlow: Longman Sci Tech,1989

[3]Bahri A,Coron J M.On a nonlinear elliptic equation involving the critical Sobolev exponent:the efect of topology of the domain.Comm Pure Appl Math,1988,41:255-294

[4]Bahri A,Li Y Y,Rey O.On a variational problem with lack of compactness:the topological efect of the critical points at infnity.Calc Var Partial Difer Equ,1995,3:67-94

[5]Ben Ayed M,Hammami M.On a fourth order elliptic equation with critical nonlinearity in dimension six. Nonlinear Anal,2006,64(5):924-957

[6]Ben Ayed M,El Mehdi K.The Paneitz Curvature problem on lower dimentional spheres.Ann Global Anal Geom,2007,31(1):1-36

[7]Ben Ayed M,El Mehdi K,Grossi M,Rey O.A nonexistence result of single peaked solutions to a supercritical nonlinear problem.Comm Contemp Math,2003,5:179-195

[8]Ben Ayed M,Chtioui H,Hammami M.A Morse lemma at infnity for Yamabe type problems on domains. Ann Inst Henri Poincar´e(Analyse non-lin´eaire),2003,20(4):543-577

[9]Ben Ayed M,El Khalil M,Hammami M.Some existence results for a Paneits type problem via the theory of critical points at infnity.J Math Pures Appl,2005,84:247-278

[10]Brezis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm Pure Appl Math,1983,36:437-477

[11]Brezis H,Peletier L A.Asymptotics for elliptic equations involving the critical growth//Colombani F, Modica L,Spagnolo S,eds.Partial Diferential Equations and the Calculus of Variations.Birkhauser,1989: 149-192

[12]Chabrowski J,Yan S.Concentration of solutions for a nonlinear elliptic problem with nearly critical exponent.Top Methods Nonl Anal,1999,13:199-233

[13]Chang Sun-Yung A.On Paneitz operator-a fourth order diferential operator in conformal geometry//Christ M,Kenig C,Sadorsky C,eds.Harmonic Analysis and Partial Diferential Equations;Essays in Honor of Alberto P.Calderon.Chicago Lectures in Mathematics,1999:127-150

[14]Chow S N,Hale J K.Methods of bifurcation theory.Grundl Math Wiss,Vol 251.Berlin:Springer,1982

[15]Del Pino M,Felmer P,Musso M.Two bubles solutions in the supercritical Bahri-Coron’s problem.Calc Var Partial Difer Equ,2003,16:113-145

[16]Del Pino M,Felmer P,Musso M.Multi-peak solutions for supercritical elliptic problems in domains with small holes.J Difer Equ,2002,182:511-540

[17]Djadli Z,Hebey E,Ledoux M.Paneitz type operators and applications.Duke Math J Partial Difer Equ, 2000,104:129-169

[18]Ebobisse F,Ahmedou M O.On a nonlinear fourth-order elliptic equation involving the critical Sobolev exponent.Nonlinear Anal TMA,2003,52:1535-1552

[19]Gazzola F,Grunau H C,Squassina M.Existence and nonexistence results for critical growth biharmonic elliptic equations.Calc Var Partial Difer Equ,2003,18:117-143

[20]Hammami M.Concentration Phenomena for Fourth order elliptic equations with critical exponent.Elec J Difer Equ,2004,2004:1-22

[21]Han Z C.Asymptotic approach to singular solutions for nonlinear elliptic equations involving critical Sobolev exponent.Ann Inst Henri Poincar´e(Analyse non-lin´eaire),1991,8:159-174

[22]Lin C S.Classifcation of solutions of a conformally invariant fourth order eqution in Rn.Comm Math Helv,1998,73:206-231

[23]Mehdi K,Selmi A.Concentration and multiplicity of solutions for Fourth order equation with critical nonlinearity.Nonlinear Anal TMA,2006,64:417-439

[24]Melo J L F,Santos E M D.Positive solutions to a fourth-order elliptic problem by the Lusternik-Schnirelmann category.J Math Anal Appl,2014,420:532-550

[25]Micheletti A M,Pistoia A.Existence of blowing-up solutions for a slightly subcritical or slightly supercritical nonlinear elliptic equation on Rn.Nonlinear Anal TMA,2003,52:173-195

[26]Musso M,Pistoia A.Multispike solutions for a nonlinear elliptic problem involving the critical Sobolev exponent.Indiana Univ Math J,2002,51:541-579

[27]Musso M,Pistoia A.Dowble Blow-up solutions for a Brezis-Nirenberg type problem.Comm Contemp Math,2003,5:775-802

[28]Rey O.Bifurcation from infnity in a nonlinear elliptic equation involving the limiting Sobolev exponent. Duke Math J,1990,60:815-861

[29]Rey O.The role of Green’s function in a nonlinear elliptic equation involving the critical Sobolev exponent. J Funct Anal,1990,89:1-52

[30]Rey O.Proof of two conjectures of H.Brezis and L.A.Peletier.Manuscripta Math,1989,65:19-37

[31]Rey O.Blow-up points of solutions to elliptic equations with limiting nonlinearity.Difer Integral Equ, 1991,4:1155-1167

[32]Rey O.The topological impact of critical points at infnity in a variational problem with lack of compactness: the dimension 3.Adv Difer Equ,1999,4:581-516

[33]Van der Vorst R C A M.Variational identitie and applications to diferential systems.Arch Rational Mech Anal,1991,116(4):375-398

[34]Van der Vorst R C A M.Fourth order elliptic equations with critical growth.C R Acad Sci Paris,1995, 320:295-299

Appendix

In this appendix,we collect the estimates of the diferent integral quantities presented in the paper.These estimates are originally introduced by Bahri[2]and Bahri and Coron[3].For the proof,we refer the interested reader to the literature[2,3,5,29].In this appendix,we suppose that λidiis large enough and εijis small enough.

Lemma A.1We have the following estimates:

where Sn,c2and c3are defned in Proposition 2.2.

Lemma A.2The following estimates holds:

∗Received April 8,2014;revised October 18,2014.