自适应细菌觅食算法在优化问题中的应用
2015-02-10肖文显褚镭郦王俊阁马孝琴
肖文显,褚镭郦,王俊阁,刘 震,马孝琴
细菌觅食算法[1-2](bacterial f oraging al gorith m,简称BFA)是由 K.M.Passino于2002年根据生物学中人类肠道内大肠杆菌或者粘细菌在觅食过程中体现出的智能行为,经过人工抽象而提出的一种智能随机搜索算法.算法虽然起步较晚,但是应用比较广泛[3-6].尽管BFA算法在求解低维优化问题时具有较好的搜索性能,但是随着问题维数的上升和复杂程度的加大,固定的步长和固定的驱散概率使算法在后期容易陷入局部最优解而产生早熟现象[7-9].针对该问题,作者提出自适应步长策略,通过动态调整步长,使趋向操作能够不断调整并适应算法的进化程度.作者提出自适应驱散概率策略,避免BFA算法固定驱散概率带来的优质解流失问题,确保算法在后期不但保有较好种群多样性而且具有稳定的收敛能力.
1 细菌觅食算法
BFA算法模拟细菌觅食中一边感应周边事物浓度变化一边进行趋近或者远离的机制,分别设计了趋向、聚集、复制和驱散4种行为[10-12].
1.1 趋 向
趋向行为是模拟大肠杆菌依靠鞭毛旋转方式表现出的两种不同的位置移动方式,分别为翻转和游动.翻转是指寻找新的方向,游动是指保持方向不变的前进.具体操作如下:首先朝某随机方向游动一个单位步长,如果新位置的适应值比之前增加,则继续沿着该方向游动;如果新位置的适应值比之前降低,则进行旋转操作,朝另一个随机方向游动.当达到最大尝试次数后,停止趋向操作.细菌趋向操作表示如式(1)所示
其中:θi(j,k,l)为第i个细菌的位置,j、k、l分别表示细菌个体完成趋向、复制和驱散的次数;C(i)为第i个细菌进行游动的步长;Δ(i)为分量在[-1,1]之间的随机向量.
1.2 聚 集
细菌群落在觅食过程中,会通过调整细胞与细胞之间的引力和斥力,从而使细菌在具有聚集特性的情况下又保持各自相对独立的位置.引力使细菌聚集在一起,而斥力使得细菌分散在相对独立的位置上获取食物.BFA算法模拟这种聚集行为,数学表达式如下
其中:P(j,k,l)={θi(j,k,l)i=1,2,…,S}为细菌群落;JCC(θ,P(j,k,l))为细菌群落之间传递信号的影响值;da为引力深度;wa引力宽度;dr为斥力高度;wr为斥力宽度.
在趋向循环中加入聚集操作后,第i个细菌的适应值应叠加传递信号影响值JCC,具体计算公式为
1.3 复 制
在细菌群落进化到一定程度后,根据自然选择的“优胜劣汰”理论,部分觅食能力较弱的细菌会被自然淘汰.同时,细菌群落会通过繁殖来保证种群规模的稳定.BFA算法以复制操作来模拟细菌群落的这种生物现象.
对于确定的k、l以及每个细菌i=1,2,…,S,定义细菌i的能量函数为
通过细菌的能量函数值来衡量细菌的觅食能力.Jienergy越大,说明细菌i的觅食能力越强;反之,细菌i的觅食能力越弱.将细菌按其能量Jienergy从大到小进行排列,淘汰掉后一半能量较小的细菌个体,然后将前一半能量较大的细菌群落中的每个个体均复制,从而生成与原细菌群落规模一致的新的具有较强觅食能力的细菌群落.
1.4 驱 散
在算法经过若干代复制后,细菌以给定的概率进行驱散操作,被选中的细菌会随机重新分配到新的位置.即若细菌群落中的某个细菌个体满足驱散发生的概率,则这个个体失去原有觅食位置,在解空间中随机选中一个新位置,由此形成了一个崭新个体.
2 自适应细菌觅食算法
2.1 自适应趋向步长
趋向操作使BFA算法具有局部搜索能力,但是固定的步长又使算法存在一定缺陷:首先,步长的大小不易确定.步长太大,虽然算法收敛速度较快,但是搜索的跳跃性太大,算法不易找到最优解.步长太小,算法虽然局部搜索精度较高,但算法的寻优过程将非常漫长.
针对该问题,文献[13]等提出采用自适应的方式调整步长,取细菌个体的步长等于周围临近个体中最大距离和最小距离的平均值与随机数的乘积.但是,这种调整方式仅仅依赖最大距离和最小距离两个细菌个体信息,步长调整的导向作用不明显.因此,作者综合考虑细菌个体的觅食能力(能量函数)和最大、最小距离个体对细菌个体的影响,并将上述参数进行耦合,提出步长调整参数A,如式(5)所示
其中:Ji为第i个细菌的适应值;Xmax、Xmin为变量的边界值.
自适应调整算法在运行过程中的趋向步长,从而达到局部搜索和全局寻优的平衡.步长自适应调整如式(6)所示
其中:Iteri、Itermax分别为迭代次数和最大迭代次数.
2.2 自适应驱散概率
BFA算法中的驱散操作以一个固定的概率P将细菌群体中的部分个体进行重新位置分配,借此改善细菌群落的种群多样性.但是,对于那些位置靠近全局最优值的优秀个体而言,驱散操作很可能使其丢失原有位置,被驱散至较差的一个新位置.这样的算法进化过程实质上是一种退化.
因此,论文提出一个自适应驱散概率Pself,所有细菌个体均按照式(7)的动态概率进行自适应驱散
其中:Jienergy、Jmaxenergy、Jminenergy分别为细菌i的能量值、能量上限、能量下限.
2.3 自适应细菌觅食算法求解步骤
综上所述,对于最小化的优化问题,自适应BFA算法的执行步骤如下:
第1步:参数初始化.
第2步:初始化细菌位置.在问题可行域内随机生成初始解,计算细菌个体的适应值.
第3步:驱散循环、复制循环、趋向循环.
第4步:执行趋向操作.按式(5)、(6)自适应调整趋向步长,当适应值上升时,保持游动方向,当适应值下降时,进行旋转,重新选定方向.若达到趋向操作次数上限,则跳出趋向循环,并执行第5步.
第5步:执行复制操作.
第6步:执行驱散操作.按式(7)所示动态概率进行自适应驱散.
第7步:判断算法是否满足收敛条件,若收敛,则输出结果并结束;若不满足收敛条件,则返回第3步.
3 算 例
3.1 测试函数
为验证改进算法的可行性和有效性,论文采用如下测试函数对上述算法进行对比测试.
(1)Sphere函数
(2)Rosenbr ock函数
(3)Rastrigrin函数
(4)Griewank函数
(5)Ackley函数
实验设置的参数如下:
(1)函数维数N分别取5、10、20、30、50维5种方案,由于篇幅限制在此仅列出50维时的模拟计算结果;
(2)细菌总数S=50;趋向次数为50;复制次数为3;驱散次数为2;初始游动步长C=0.001R(R为优化区间宽度);驱散概率P=0.25.
上述5个标准测试函数的理论最优值均为0.论文分别采用BFA和自适应BFA算法对上述5个测试函数进行50次优化计算,取优化结果的平均值作为衡量指标.同时,为验证论文提出改进算法的有效性,以遗传算法对上述5个标准测试函数进行50次求解,取其平均值作为算法之间的横向比较,结果如表1所示.
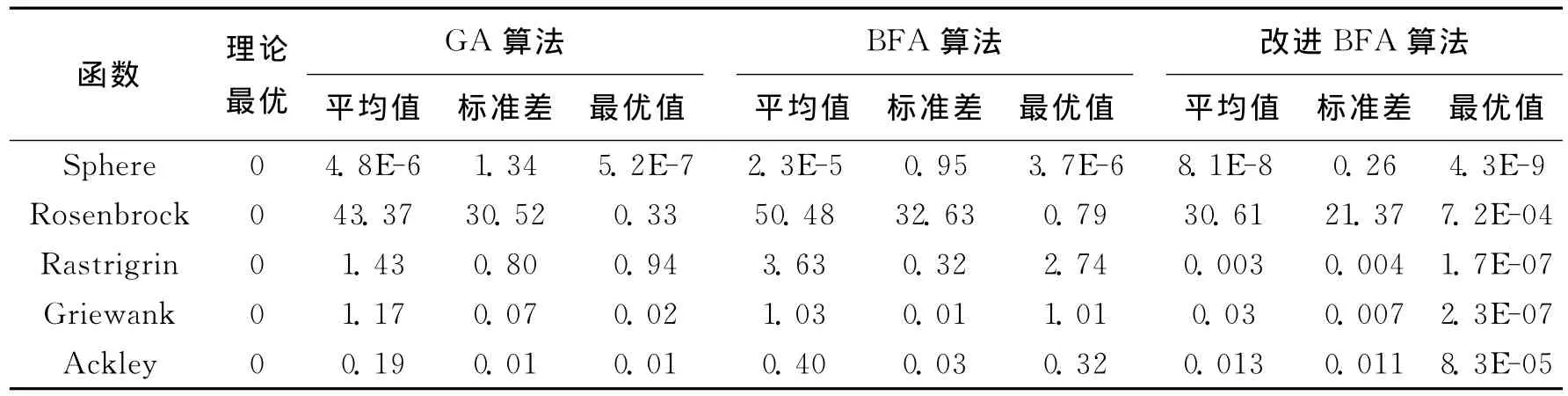
表1 函数优化结果对比Tab.1 Comparison of results of benchmark functions
对比表1中的平均值和最优值,可以看出:改进的BFA算法所得到的平均值、最优值均小于标准BFA算法.由此可见,通过引入自适应动态步长和自适应调整驱散概率,改进BFA算法能够寻找到更加优秀的解.对比表1中的标准差,可以看出改进BFA算法结果的标准差同样小于标准BFA算法,可见改进后的算法在求解的稳定性方面也优于标准BFA.对比改进BFA算法与GA算法的计算结果可见,改进BFA算法求解得到的平均值和最优值优于GA算法,同时前者多次求解结果的标准差也小于后者,说明论文提出的改进BFA算法的全局寻优能力优于GA等智能优化算法.
将BFA算法和改进BFA算法求解上述5个测试函数的迭代过程记录并进行对比,如图1所示,其中迭代过程取值为多次计算的平均值.
由图1可见,改进的BFA算法在求解测试函数时,可以以更少的计算消耗得到质量更高的寻优结果,并且在迭代计算后期,改进的BFA算法能够保持继续探索新空间的能力,避免了陷入局部最优解.
3.2 TSP问题
为进一步验证论文提出的改进BFA算法的有效性和适用性,对于Oliver TSP30个城市(已知最优解为423.74)和TSP50个城市(已知最优解为427.86),分别采用标准BFA算法和改进BFA算法进行求解,参数设置与3.1中相同,取50次计算结果的平均值作为衡量指标,结果如表2所示.

表2 TSP30和TSP50问题运行结果Tab.2 Results of TSP30 and TSP50
对比表2中两种算法所得的最优解可见,改进的BFA算法能够搜索到更加优秀的解.对比平均值可见,改进BFA算法的求解性能的稳定性要高于标准BFA算法.随着城市数量的增加,问题变得更加复杂,对比TSP50的计算结果可见,改进BFA算法在求解复杂程度高的问题时,寻优效果要优于标准BFA算法.上述结论与3.1测试函数得到的结果一致,再次证明了论文提出的改进BFA算法的可行性和有效性.
4 结束语
为解决BFA算法固定趋向步长和固定驱散概率所带来的缺陷,论文采取自适应调整趋向步长的策略,随着搜索的不断深入,趋向步长逐渐变小,算法得以在更精细的范围内进行搜索.同时,论文提出驱散概率的自适应调整,将细菌进行驱散的概率的大小与其具有的能量对应,在保证种群多样性的基础上,进一步避免了优秀个体的流失.通过4个测试函数的模拟计算和在TSP30、TSP50中的应用,验证了论文提出的改进算法的可行性和有效性,改进的BFA算法性能优于标准BFA算法,适用于求解复杂优化问题.
[1] Dong H K,Ajith A,Jae H C.A hybrid genetic algorith m and bacterial f oraging approach f or global opti mization[J].Infor mation Sciences,2007,177(2):3918-3937.
[2] Swagatam D,Arijit B,Sambarta D.Bacterial foraging opti mization algorith m:theoretical foundations,analysis,and applications[J].Foundations of Computer,2009,3:23-55.
[3] 马溪原,吴耀文,方华亮,等.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J].中国电机工程学报,2011,31(25):17-25.
[4] 崔静静,孙延明,车兰秀.改进细菌觅食算法求解车间作业调度问题[J].计算机应用研究,2011,28(9):3324-3326.
[5] 李丹,唐普英.基于细菌觅食的盲源分离算法研究[J].通信技术,2011,44(12):150-152.
[6] 王雪松,程玉虎,郝名林.基于细菌觅食行为的分布估计算法在预测控制中的应用[J].电子学报,2010(2):333-339.
[7] 肖文显,许利军,马孝琴.混沌差分进化算法在复杂优化问题中的应用研究[J].安徽大学学报:自然科学版,2014,38(3):32-36.
[8] 郑慧涛,梅亚东,胡挺,等.双层交互混合差分进化算法在水库群优化调度中的应用[J].水力发电学报,2013,32(1):54-62.
[9] 周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21.
[10] 刘小龙.细菌觅食优化算法的改进及应用[D].广州:华南理工大学工商管理学院,2011.
[11] 胡洁.细菌觅食优化算法的改进及应用研究[D].武汉:武汉理工大学理学院,2012.
[12] 许鑫.细菌觅食优化算法研究[D].长春:吉林大学计算机科学与技术学院,2012.
[13] 李珺,党建武,卜锋.自适应步长的细菌觅食优化算法研究[J].兰州交通大学学报,2013,32(6):10-14.
