第3类边界条件下1维平板对流融化过程的量纲一分阶段求解

孟凡康，于 航

（1.同济大学机械与能源工程学院，上海201804；2.辽宁工程技术大学建筑工程学院，辽宁阜新123000）

第3类边界条件下1维平板对流融化过程的量纲一分阶段求解

孟凡康1，2，于 航1

（1.同济大学机械与能源工程学院，上海201804；2.辽宁工程技术大学建筑工程学院，辽宁阜新123000）

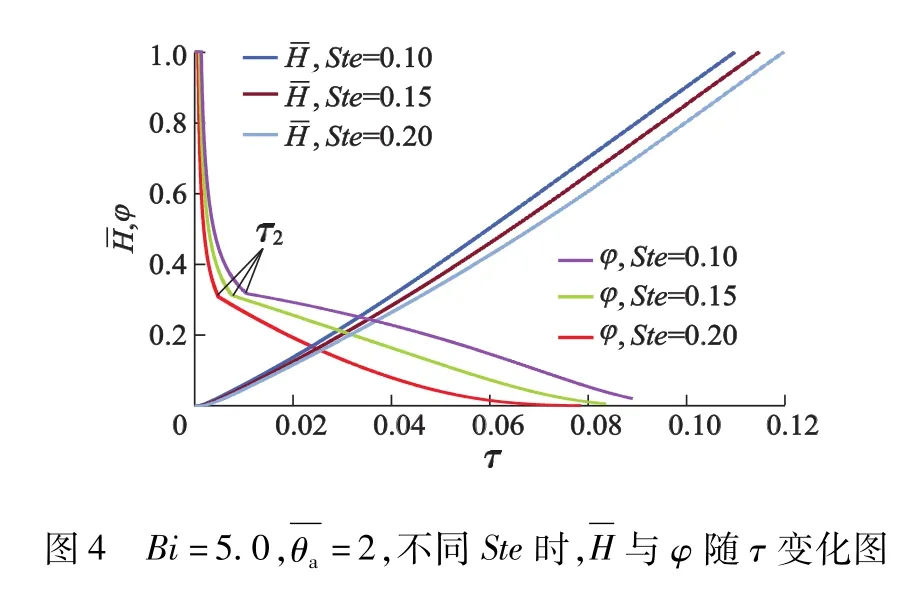
为了研究平板融化各个传热阶段的特性，以第3类边界条件下1维有限厚度平板对流融化过程为研究对象，同时考虑融化后的相变材料被周围流体及时带走，把传热过程分成3个阶段，分别建立了传热计算模型，并采用3次多项式热平衡积分方法对各阶段进行近似求解.利用推导的计算方法，以Stefen数（Ste）、Biot数（Bi）及量纲一环境温度为控制参数对相界面变化规律进行了讨论，结果表明：当时，平板融化过程可以分为3个阶段，相反，可以分为2个阶段；在不同控制参数条件下，融化开始阶段量纲一相界面位置与量纲一时间（т）变化率相对较小，而融化后期变化率较大，且近似呈线性关系；在其他控制参数不变的条件下，随着Ste的增小，Bi或的增加，整个融化过程的总融化量纲一时间减小，且与т变化率增大.

1维平板；融化传热；分阶段；热平衡积分法；第3类边界条件

固液相变问题在自然界和工业领域非常广泛［1-4］.其中，外融冰蓄冰槽中水流直接冲刷冰体表面就是其中典型的固液相变问题.该问题属于第3类边界条件下的对流相变基础科学问题.对于此类问题的研究有利于指导工程实际应用.

相变问题的求解方法，可以分为精确解法和近似解法.目前精确求解方法只存在于一些模型和边界条件都非常简单的情况［5-7］.近似解法主要包括准稳态法［8］、摄动法［9］、热阻法［10］、逐次逼近法［11］和多项式热平衡积分法［1，12-14］等.采用多项式热平衡积分方法是一种解决相变传热问题的典型方法. T.R.Goodman［12］利用2次多项式热平衡积分法求解偏微分方程方法求解了几个典型的1维相变问题，其中包括有限厚度平板凝固问题的近似解.C. D.Ho等［13］研究了空气外掠半无限大冰层融化换热问题，整个换热过程分成了融化前和融化后2个阶段，采用2次多项式热平衡积分方法对冰层内的温度场进行了近似求解.T.G.Myers等［14］采用3次多项式热平衡积分方法，分别研究了1维有限厚度平板的相变问题和直接接触相变问题［1］.文献［14］中，平板两侧分别施加不同第3类边界条件，按照融化过程传热特性，把相变过程分成4个阶段.其研究对象是放置在空气中的相变材料，即融化后的相变材料在表面形成一层液体传热层.文献［1］中考虑的是直接接触相变传热问题，把相变过程分成3个阶段.文献［1，14］均分阶段推导了计算模型，同时验证了3次多项式热平衡积分法相对于2次多项式、指数热平衡积分法等具有更高的计算精度.

区别于已有文献，笔者以第3类边界条件下，1维有限厚度平板对流融化过程为研究对象，同时考虑融化后的相变材料被周围流体及时带走，按照平板内部融化传热温度变化规律，把传热过程分成3个阶段，采用3次多项式热平衡积分方法进行近似求解.以Ste，Bi及为控制参数对相界面变化规律进行讨论.该方法具有形式简单，方便编程的特点，且能够从相变平板整个融化过程来分析各阶段传热特征.

1 物理模型

研究对象如图1所示，无限大平板厚度为H，平板的融点温度为θm，环境温度为θa，θa＞θm，对流换热系数为h，平板的初始温度为θ0，θ0＜θm，上部（z=H）绝热.整个传热过程中，热量由下部（z=0）环境通过对流换热传递给平板内部，从而使得内部各点温度上升.平板的导热系数为λ，密度为ρ，融化潜热为L，流体的导温系数为a.

图1 1维有限厚度平板模型

只讨论如下情况：下部边界开始融化时，温度渗透深度还没有达到上部边界，即上部边界温度一直维持在初始温度.按照融化时间顺序，融化过程可以分为3个阶段，如图2所示.

图2 对流融化过程3个阶段温度分布示意图

第1阶段（图2a），即Phase1，从平板与外界环境之间开始传热为起点（t=0），下部边界温度达到融点温度为终点（t=t1），此阶段中温度渗透深度为δ0，当t=t1时，δ0＜H；第2阶段，即Phase2（图2b），从t1开始，到平板上部边界温度开始上升（t=t2）结束，此阶段中温度渗透深度为δ1，下部相界面的位置为H1，当t=t2时，δ1=H；第3阶段（图3c），即Phase3，从t2开始，平板融化完毕（t=t3）结束，下部相界面的位置为H2.

2 求解过程

采用3次多项式热平衡积分法对平板内部温度场进行近似求解.温度分布方程为

式中：A，B，C，δ（t）为4个未知数，下文将根据各个阶段的具体条件分别求出.

2.1 Phase1阶段分析

在本阶段，平板还没有融化.温度渗透深度至平板上部边界范围内（［δ0，H］），温度维持θ0.当下边界的温度达到θm时，该阶段结束，时间为t=t1.

平板内部导热控制方程及其定解条件如下：

把方程（3）-（5）分别代入式（1）可得

平板内温度场可以表示为

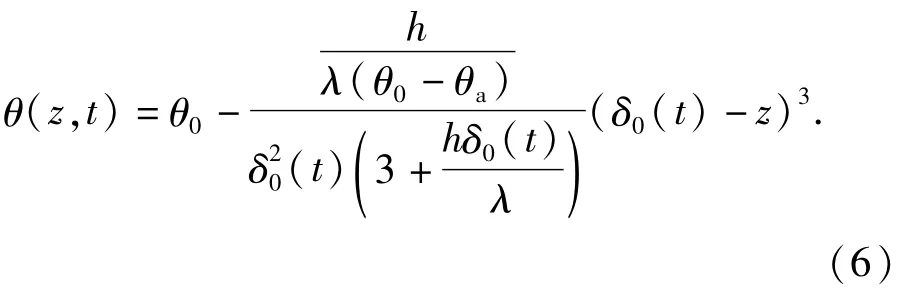
对方程（2）在z∈［0，δ0（t）］进行积分，可以获得关于δ0（t）的方程：

方程（7）有显式解如下：

当该阶段结束时t=t1，下边界的温度达到θm，根据方程（6），温度渗透深度为

该阶段结束时间t1可由方程（9）代入方程（8）获得.

2.2 Phase2阶段分析

在本阶段，平板下部开始融化，下部边界温度维持在θm.温度渗透深度至平板上部边界范围内（［δ1，H］），在此阶段同样维持在初始温度θ0不变.当上边界的温度开始上升时，该阶段结束，时间为t=t2.

由平板内部导热控制方程、边界层能量方程及其定解条件如下：

方程（12）-（14）分别代入式（1）可得

从而平板内温度场可以表示为

对方程（10）在z∈［H1，δ1（t）］进行积分，可得如下方程：

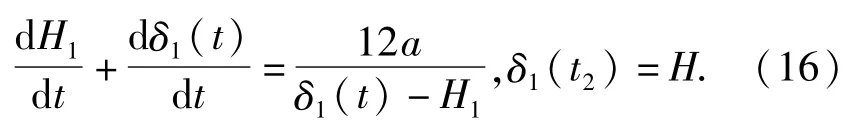
方程（11）可以表示为

经过上面的转换，方程（10），（11）转化为易于求解的常微分方程（16），（17），其中包括2个待求函数H1和δ1（t）.

2.3 Phase3阶段分析

以Phase2阶段的结束时间t2为开始，以平板融化完全为结束t=t3.温度渗透深度已经达到上边界H，上边界的温度不再维持在θ0，而是一个关于时间的函数θn（t）.

平板内部导热控制方程，边界层能量方程及其定解条件如下：

方程（20）-（22）分别代入式（1）可得

从而平板内温度场可以表示为

对方程（18）在z∈［H2，H］进行积分，可得

方程（19）可以表示为

同样经过上面的转换，方程（18）和（19）转化为易于求解的常微分方程（24）和（25），其中包括2个待求函数H2和θn（t）.

引入量纲一方法有利于问题的研究［15］，对式（16），（17），（24）和（25）按下列各式分别进行量纲归一，进而可以获得形式简单，便于编程的公式：

式中φ为显热量与总换热量的比值.

式（26）-（29）所采用的数值求解方法，均采用显式差分格式，并验证消除了量纲一时间对于求解结果的影响.

3 验 证

以第3类边界条件下，1维有限厚度平板对流融化过程为研究对象，同时考虑了融化后的相变材料被周围流体及时带走，很难找到相同研究对象、相同定解条件的文献，进行整个融化过程的验证.但应用文中的方法，平板厚度假设为无穷大，可以与文献［13］中计算结果进行对比，验证Phase1和Phase2这2个阶段的正确性.

采用文献［13］中的计算参数：速度v=10 m· s-1，冰层长度L=20 m，冰层初始温度θ0=-20℃，空气温度θa=30+5sin（πt/t0），t0=10 h，Num=

图3为文中与文献［13］计算结果验证图，表示量纲一融冰层厚度随时间的变化，量纲一融冰层厚度为

式中：l为融化厚度；δl为温度渗透距离.

图3 文中与文献［13］计算结果验证图

从图3可以看出：2种方法计算的量纲一融化冰层厚度随时间的变化规律相同，其最大相对误差为4.8％.说明Phase1和Phase2这2个阶段的计算方法是正确的.

4 分析与讨论

在Phase1阶段，由式（9）可得，当H≤δ0（t1）=时，即温度渗透深度已经达到平板上部边界，此时没有Phase2阶段，这种情况由于篇幅所限不予讨论，可见是判别融化过程分为2个阶段或者3个阶段的依据.

5 结 论

3）在其他控制参数不变的条件下，随着Ste的增小，Bi或的增加，整个融化过程的总融化量纲一时间减小，且与т变化率增大.

（

）

［1］Myers T G，Mitchell S L，Muchatibaya G.Unsteadycontactmelting of a rectangular cross-sectionmaterial on a flat plate［J］.Physics of Fluids，2008，20：103101-1-12.

［2］Choi IS，Kim JD，Kim E，et al.Experimental characteristics of a storage tank on a harvest-type ice storage system［J］.International Journal of Heat and Mass Transfer，2002，45（7）：1407-1412.

［3］Soltan B K，ArdehaliM M.Numerical simulation ofwater solidification phenomenon for ice-on-coil thermal energy storage application［J］.Energy Conversion and Management，2003，44（1）：85-92.

［4］Yamaha M，Nakahara N，Chiba R.Studies on thermal characteristics of ice thermal storage tank and a methodology for estimation of tank efficiency［J］.International Journal of Energy Research，2008，32（3）：226-241.

［5］Lunadini V J.Heat Transfer in Cold Climate［M］.New York，USA：Van Nostrand Reinhold Company，1981.

［6］Ei-Genk M S，Cronenberg AW.Solidification in a semiinfinite region with boundary conditions of the second kind：an exact solution［J］.Letters in Heat and Mass Transfer，1979，6（4）：321-327.

［7］Özisik M N.Heat Conduction［M］.New York，USA：John Wiley and Sons，Inc，1980.

［8］Cheng K C，Inaba H，Gilpin R R.Effects of natural convection on ice formation around an isothermally cooled horizontal cylinder［J］.Journal of Heat Transfer，1988，110（4）：931-937.

［9］Pedroso R I，Domoto G A.Exact solution by perturbation method for planar solidification of a saturated liquid with convection at the wall［J］.International Journal of Heat and Mass Transfer，1973，16（9）：1816-1819.

［10］陈则韶.求解凝固相变热传导问题的简便方法：热阻法［J］.中国科学技术大学学报，1991，21（3）：69-76. Chen Zeshao.A simple heat-resistance method for the solution to heat conduction undergoing solidification［J］.Journal of China University of Science and Technology，1991，21（3）：69-76.（in Chinese）

［11］Savino JM，Siegel R.An analysis of the transient solidification of a flowing liquid on a convectively cooled wall［C］∥Proceedings of the Third International Heat Transfer Conference.NewYork，USA：［s.n.］，1962：123-127.

［12］Goodman T R.The heat-balance integral and its application to problems involving a change of phase［J］. Transactions of ASME，1958，80（4）：335-342.

［13］Ho CD，Yeh H M，WangW P，etal.Cool thermal discharge obtained with air flowing overmelting ice by complete removal ofmelt［J］.International Journal of Heat and Mass Transfer，2000，27（6）：785-794.

［14］Myers TG，Mitchell SL，Muchatibaya G.A cubic heat balance integralmethod for one-dimensionalmelting of a finite thickness layer［J］.International Journal of Heat and Mass Transfer，2007，50（25）：5305-5317.

［15］王颖泽，宋新南.弹性体受热冲击作用的热力耦合特性分析［J］.江苏大学学报：自然科学版，2014，35（2）：183-188. Wang Yingze，Song Xinnan.Thermo-mechanical coupling characteristics on elastic solid subjected to thermal shock［J］.Journal of Jiangsu University：Natural Science Edition，2014，35（2）：183-188.（in Chinese）

（责任编辑 贾国方）

M ultistage solving of one-dimensional platemelting convection process by dimensionlessmethod under third boundary condition

Meng Fankang1，2，Yu Hang1
（1.School of Mechanical and Energy Engineering，Tongji University，Shanghai 201804，China；2.School of Architecture Engineering，Liaoning Technical University，Fuxin，Liaoning123000，China）

To investigate the characteristics of each melting heat transfer process of plate，the onedimensional convectivemelting process of a finite thickness layer was solved under the third boundary condition，and the phase change material was considered to be taken away by the surrounding fluid in time aftermelting.The heat transfer processwas divided into three stages，and calculation model of each heat transfer stage was built respectively.A cubic heat balance integralmethod was used to obtain the approximate solution of each stage.The changing regulation of phase interface was discussed with Stefen number（Ste），Biot number（Bi）and dimensionless temperature of environmenas control parameters.The results show that the platemelting process can be divided into 3 phases in the condition of Bion the contrary，it can be divided into 2 phases.For different control parameters，the changing rates of dimensionless position of the phase interfaceand dimensionless time（т）arerelatively small at the beginning ofmeltingwith big linear changing rate at latter stage.When other control parameters are unchanged，with the decreasing of Ste and increasing of Bi orthe total melting dimensionless time is decreased，while the change rates ofand т are increased.

one-dimensional plate；melting heat；multistage；heat balance integral method；third boundary condition

TK02

A

1671-7775（2015）05-0533-06

孟凡康，于 航.第3类边界条件下1维平板对流融化过程的量纲一分阶段求解［J］.江苏大学学报：自然科学版，2015，36（5）：533-538.

10.3969/j.issn.1671-7775.2015.05.007

2014-12-22

世界银行/全球环境基金资助项目（1-A-CS-014）

孟凡康（1979—），男，江苏淮安人，博士研究生（mfk3999147@126.com），主要从事外融冰相界面移动规律研究.

于 航（1963—），女，上海人，教授，博士生导师（yuhang@tongji.edu.cn），主要从事蓄能和空调热湿传递理论研究.