基于重心基准的平面坐标转换

范方标

（深圳市岩土综合勘察设计有限公司，广东深圳518100）

基于重心基准的平面坐标转换

范方标

（深圳市岩土综合勘察设计有限公司，广东深圳518100）

在工程测量领域，实现新旧坐标系之间的顺利转换是充分利用以前测绘成果的关键，是绘制各种比例尺地图的基础。本文以平面坐标转换为例，介绍平面直角坐标转换模型，并根据实际生产实践分析该模型中存在的病态现象，据此提出一种重心基准的平面坐标转换模型，同时将这两种模型进行对比分析，提出了修正平面直角坐标转换模型的方法，并通过工程实例分析转换结果和精度。

坐标转换；重心；参数；矩阵

0 引 言

我国大地坐标系主要有北京54坐标和西安80坐标系，后者只对一等点和二等点进行布测，因此对三、四等点的布测只能利用北京54坐标。然而在实际测绘工程中，当需要对三、四等点进行布测时，要将西安80坐标转换为北京54坐标，因此选择正确的转换模型是保证转换可靠性的基础，关系到测量结果的精确性。

1 坐标转换概述

坐标转换包括参心坐标转换、不同地心坐标转换，参心坐标与地心坐标之间的转换、相同坐标系的直角坐标与大地坐标转换、大地坐标与高斯平面坐标转换等[1］。对二维坐标系转换来说：如果空间中的两个直角坐标系原点相同，在经过三次旋转后，可实现两个坐标系的重合；若两个坐标系的原点处于不同位置，那么通过坐标轴的平移和旋转可实现两个坐标系的重合；若两个坐标系之间还存在尺度的不同，那么则需要进行尺度缩放。因此二维坐标系的转换参数包括平移、旋转、尺度等。

由于转换模型非常严密，故而在实际生产实践中，利用数学转换模型转换北京54、西安80、WGS－84等坐标系而得到的结果与实际存在较大差异。出现这一现象的原因是：由于自由网平差缺少起算数据，因此往往通过附加条件、约束条件解决平差基准问题。通过对比分析坐标转换模型和重心基准条件方程发现，二者在形式上非常类似。因此，如何将重心基准条件应用到坐标转换中，是生产实践中需要重点解决的课题。

2 转换矩阵状态

现假设某点在原坐标系下的坐标为（x1，y1），对应到新坐标系下的坐标为（X，Y），而原坐标系的原点对应到新坐标系的坐标为（x0，y0），同时原坐标系与新坐标系的轴夹角为α，尺度参数为m，因此转换模型为

X＝x0＋x1mcos a－y1msin a，

Y＝y0＋y1mcos a＋x1msin a.（1）

为简化矩阵的形式，现假设x0＝a，y0＝b，mcosα＝c，msinα＝d，则

X＝a＋x1c－y1d，

Y＝b＋y1c＋x1d.（2）

可将转换模型写成矩阵形式

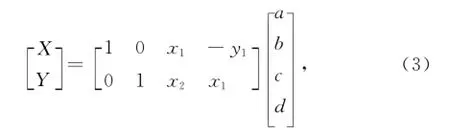
式中：a、b表示平移参数；c、d 表示缩放参数和旋转参数综合作用下的参数，而要想解出这4个未知参数，至少需要这两个坐标系的2个公共点。假设这两个坐标系中有k（k＞2）的公共点，那么从前面的矩阵中可以得出2k个误差方程，利用最小二乘原理求解4个转换参数。现假设：

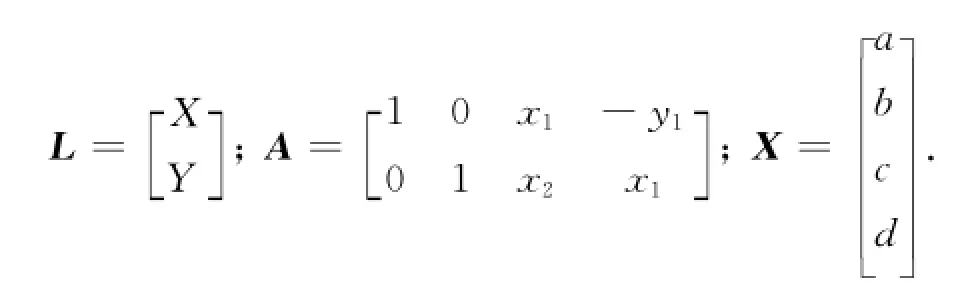
写成

AX＝L＋V，（4）

式中：A表示系数矩阵；X表示需要求解的未知参数；V表示新坐标系坐标的改正数。可以看出；A为列满轶，根据VTPV＝min原则可求解出未知参数为

X＝（ATPA）－1ATPL＝N－1W，（5）

式中：

W＝ATPL；N为四阶满轶正定矩阵；P为一般单位矩阵，则计算出来的未知参数是唯一的；但是假如N是病态的，则解出的未知参数不可靠。

在实际工作中，平面直角坐标值x、y比较大，当以m为单位时，一般有6～7位数；而在系列矩阵A中，其他元素为0或1，因此当（x1，y1）的绝对值较大时，其列向量的长度差别非常大，使得A的矩阵条件数过大，进而使得N条件数更大，这时候的矩阵呈现出病态现象，解出的未知参数不准确，平面坐标转换不可靠。而在病态的矩阵中，即使是非常微小的扰动，都可能产生较大的误差，最终导致得出的参数不准确，使得两个坐标系难以通过旋转、位移、缩放等重合到一起[2］。

3 重心基准转换模型分析

基于重心基准的平面坐标转换矩阵为ST：

矩阵中，（x0i，y0i）表示近似坐标，其具体的计算条件为

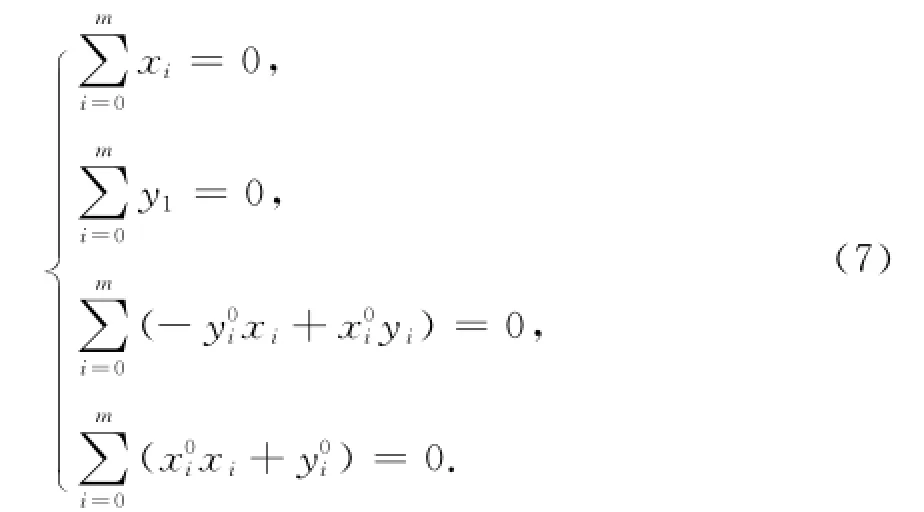
在这个计算条件中：前面两个说的是两个坐标系的重心坐标不变；第三个说的是重心到其他各点的带权向径方位角平均数不变，这里的权是重心到各点距离的平方；第四个说的是重心到其他各点的带权向径长度的平均值不变。从这四个条件中可看出，该平面坐标的转换模型是以重心为基准的，将重心作为不变量，因此中心是固定的。

将这个重心基准的转换矩阵与前文得到的坐标转换矩阵对比分析发现，二者的区别仅在于行向量顺序的变化。如果不考虑转换模型参数的物理性质，那么这两个矩阵在形式上是一致的。

在前文提到的矩阵之所以造成转换不准确是因为：在实际工作中，x和y的取值整数位数在6～7位之间，而坐标之间的平移参数整数位数只有2～3位，因此平移量非常微小，容易被人忽视。同时，平移参数对应的公共点数量非常少，与旋转和尺度参数对应的公共点相差甚远。研究表明：重心基准坐标转换模型在平差前后，其新坐标系和原坐标系的重心都没有任何变化，只不过平面直角坐标转换模型公共点转换前后的平均值之间相差一个常数，即平移参数[3］。因此，平面直角坐标转换模型解决的主要问题还是基准问题。

从上述平面直角坐标转换模型出现病态的原因来分析，解决病态的根本方法是消除掉平移参数。由于在坐标系的某一个特定区域中，转换前后的公共点重心与相对位置保持不变，因此可以建立约束条件：

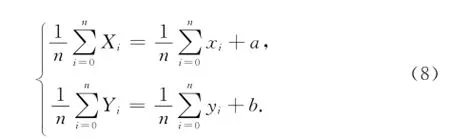
通过方程的联合求解，消除其中的平移参数（a、b），这样平面直角坐标转换模型中就只有公共点的坐标向量。此时，根据约束条件判断该模型是否处于良态，进而求解出缩放和旋转综合作用下的c、d两个参数，从而实现两个坐标系的可靠转换。

在当前的测绘领域，坐标转换多采用平面直角坐标转换模型，又被称为平面四参数模型，通过求解出a、b、c、d这四个未知参数，实现两个坐标系的顺利转换重叠。而本文提出的重心基准平面坐标转换模型将重心作为固定的不变量，通过约束条件对平面四参数模型进行相应的修正，消除a、b两个参数，使得转换模型处于良态，保证转换结果的精确度，确保工程测量工作的顺利开展[4］。

4 实例计算

某地测绘的数据原先采用的是BJ－54坐标系，将数据成果转换为80坐标系，规定比例尺为1∶10 000，精度达到1m以上。具体的转换计算可以参考下表，表1示出了以六个公共点为基准，进行参数成果转换的结果。

表1 原始数据

根据式（3）和式（5）采用最小二乘法计算；根据式（3）、式（8）、式（5），利用附加重心基准对平移参数予以消去，进而计算。结果如表2所示。

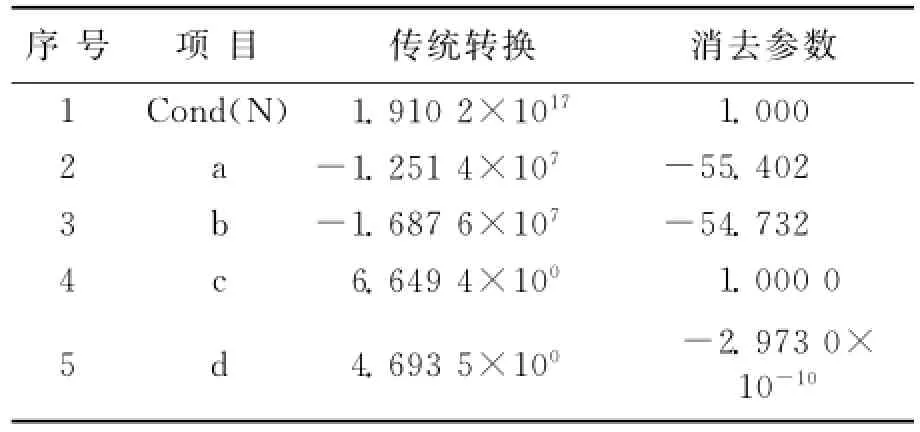
表2 矩阵条件数和转换参数结果

由表2可知，根据最小二乘方法进行计算，设计矩阵条件参数很大，该矩阵严重病态，根据式（2）计算出尺度系数，得到：m＝8 134.9＞1，说明BJ－54的坐标和80坐标之间的尺度变化率较小。而通过第二种方案进行计算，设计矩阵与方程条件数均为1，属于良态矩阵，能够予以求逆计算，得到旋转参数之后，就可以对公共点转换残差予以计算，得到最大点位误差是0.388m，满足应用需求。

除此之外，从数据精化需求角度而言，其整体残差较大，特别是第3、第6点位，误差超过了0.3 m，此两点间可能存在粗差，需要予以剔除，重新计算残差，利用剔除较大残差后计算的转换参数进行转换精度。

5 结束语

随着测绘行业的发展，社会生活中的平面坐标转换将会越来越多，研究平面坐标转换模型将成为该领域重要发展方向。利用经典最小二乘理论计算坐标转换参数在理论非常严密，但是设计矩阵的病态情况对解算结果有着一定的影响。通过对设计矩阵病态的分析，根据经典秩亏自由网平差，对比其前后重心的相对性，合理解释设计矩阵病态消除的附加条件，保证结果的可靠性。对此，本文通过对平面四参量转换模型病态的分析，利用重心基准平面坐标转换模型对病态进行修正，通过增加约束条件以消除a、b参数，从而确保坐标转换转换的可靠性。

[1]韦 铖，马文双，李明君，等.工程测量中平面坐标转换软件设计及应用[J］.测绘工程，2013，22（4）：76－79.

[2]陈绍杰，秦永洋，孙兴平，等.顾桥矿区GPS基准网高程系统转换研究[J］.测绘，2010，33（1）：34－38.

[3]彭爱文，曹佩瑶.平面坐标转换方法探讨及转换软件的设计思路[J］.测绘与空间地理信息，2007，30（3）：189－191.

[4]刘陶胜，黄声享，罗 力，等.基于重心基准的平面坐标转换研究[J］.大地测量与地球动力学，2011，31（2）：102－106.

On Plane Coordinate Transformation Based on Center of Gravity Datum

FAN Fangbiao
（Shenzhen Integrated Geological Exoloration ＆Design Co.Led，Shenzhen518100，China）

in the field of engineering measurement，to achieve a smooth transition between the old and the new coordinate system is to make full use of the key before the surveying and mapping results，is the basis for mapping various scale map.This paper takes the plane coordinate transformation as an example，introduces the plane right angle coordinate transformation model，and according to the analysis of morbid phenomena exist in the model of the actual production practice，plane coordinate transformation model proposes a benchmark，at the same time，by a comparative analysis of these two kinds of models，and put forward the method of correcting plane right angle coordinate transformation model，and through the the analysis of engineering example the conversion results and precision.

Coordinate transformation；center of gravity；parameters；matrix

P226.3

A

1008－9268（2015）01－0079－04

10.13442/j.gnss.1008－9268.2015.01.018

范方标（1978－），男，工程师，研究方向为GPS技术。

2014－06－10

联系人：范方标E－mail：1330843245＠qq.com