Matlab软件支持下的GPS基线向量网三维约束平差

王忠礼，顾刘丹，2

（1.吉林建筑大学测绘与勘查工程学院，吉林长春130118；2.云南省设计院集团勘察分院，云南昆明650228）

Matlab软件支持下的GPS基线向量网三维约束平差

王忠礼1，顾刘丹1，2

（1.吉林建筑大学测绘与勘查工程学院，吉林长春130118；2.云南省设计院集团勘察分院，云南昆明650228）

本文在对GPS基线向量网三维约束平差的数学模型进行详细引述及推导的基础上，结合某实际工程案例，利用Matlab强大的矩阵计算功能对基线向量网的三维约束平差进行了计算，解算结果与中海达HDS2003版商用软件相比较结果一致。本文可以为GPS数据处理人员以及相关专业的大中专在校学生对该内容的理解与掌握提供一定的借鉴与帮助。

GPS；基线向量网；三维约束平差；Matlab

0 引 言

目前国家重大基础设施建设如高速铁路、高速公路等工程控制网的敷设基本都已经采用静态GPS观测作为主要的定位观测技术。GPS观测技术主要包括控制网设计、外业实施以及内业数据处理等。而GPS内业数据处理主要包括基线解算、基线向量网检核以及基线网的平差等过程。用户在采用随机软件进行基线解算并检验合格之后，可以继续采用随机软件或是其他的精密GPS软件（如美国MIT的GAMMIT，美国JPL的GIPSY，瑞士的BERNESE及德国的EPOS等）或专门的GPS网平差软件（如武汉大学研制的CosaGPS）进行基线向量网的平差工作。目前大部分GPS用户都采用商用的随机GPS处理软件进行基线解算、检核及后续平差处理等[1］，然而商用的GPS网平差软件所采用的平差模型以及内部的数据处理过程往往不是用户能够及时、准确了解的，这在某些特定的应用（如高精度变形监测）上为负责数据处理的测绘人员对网平差所采用的数学模型以及数据处理的具体流程上带来了相应的担忧，再者，全国目前已经有若干高校开设了测绘工程及GIS、遥感等相关的专业，而GPS测量原理及应用一般都是这几个专业的一门主要课程。作者经过几年的授课及调查发现很多本科生对GPS内部数据处理的数学模型并不了解，这大大阻碍了学生对GPS数据处理理论与方法的掌握，因此，本文在对基线向量网的三维约束平差进行较为详尽的引述和推导的基础上，采用强大的计算软件平台Matlab7对GPS基线网的三维约束平差进行了算法的设计与实现。并采用某特定的工程为案例，以控制点的国家80坐标系的坐标作为约束条件，进行了平差的计算处理。以期为GPS数据处理的测绘人员提供相应的借鉴，为测绘及3S类专业的大中专学生提供相应的的GPS网平差模型的理解与掌握方面的帮助。

1 GPS基线向量网的三维约束平差数学模型

GPS基线向量网的三维约束平差可以在国家坐标系或地方独立坐标系中进行。约束条件可以是地面控制点的固定坐标，固定大地方位角和固定空间弦长，平差结束之后同时也进行了WGS－84坐标系到地面坐标系之间的转换[1］。对GPS控制网进行三维约束平差时，可以取GPS点的空间直角坐标为未知参数，也可以取大地坐标作为未知参数，取空间直角坐标作为未知参数的优点是误差方程的形式较为简单，便于进行后续的分析与讨论[3，4］.

GPS基线向量由84坐标向国家或地方坐标的转换往往采用布尔莎转换模型，其数学模型为

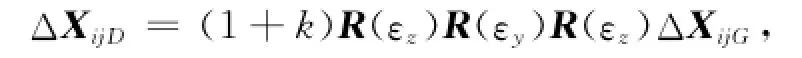
式中：ΔXijG为GPS基线向量；ΔXijD为转换到国家坐标或地方坐标的基线向量；k为尺度转换参数；εx，εy，εz为旋转参数[1］。

1.1 误差方程式的推导

布尔莎公式：

其中，

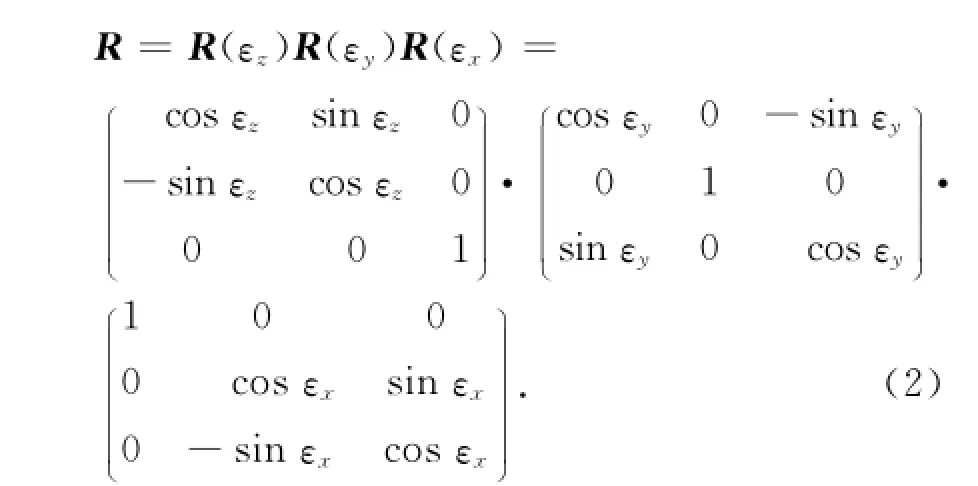
为简化计算，当k，εx，εy，εz为微小量时，忽略互乘项，且cosε≈1，sinε≈ε，则

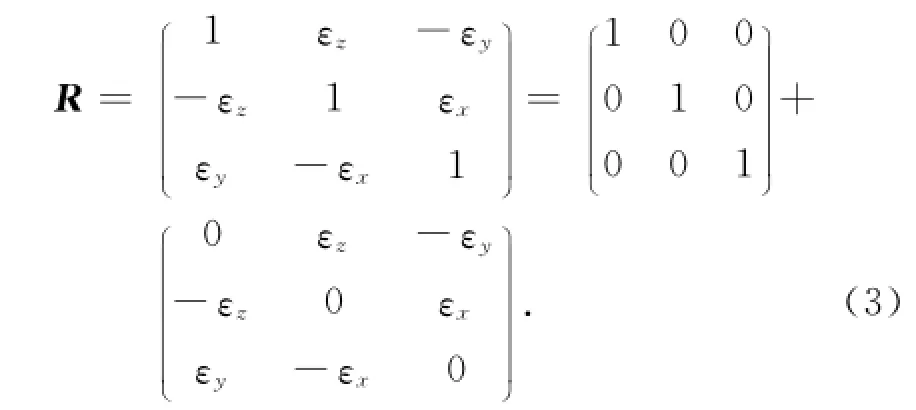
则：

因为k为微小量，忽略上式中第2项中的k，则：

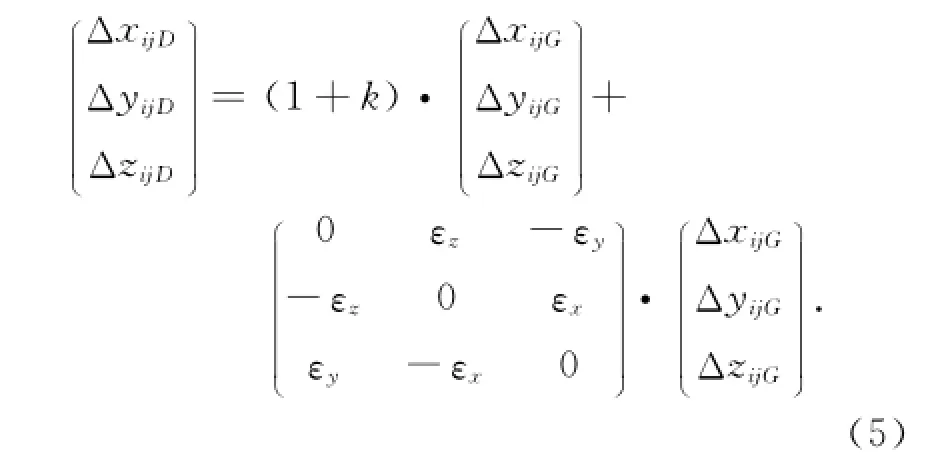
上式中的第2项可以进一步变换为

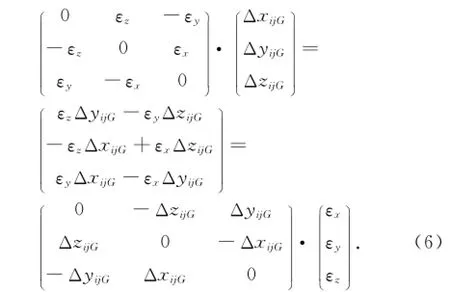
则布尔莎公式最终可以写为

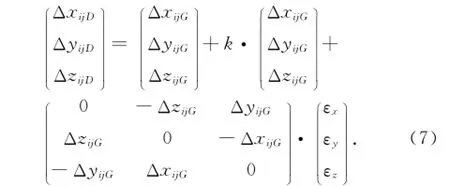
为了导出GPS基线向量的误差方程，需要进行简单的变换：

代入上式得到误差方程式为

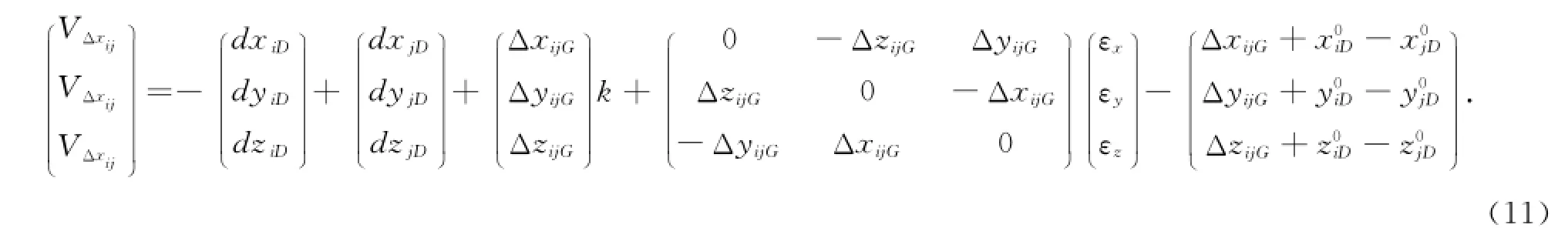
则对于每一条基线向量的误差方程式可以写成

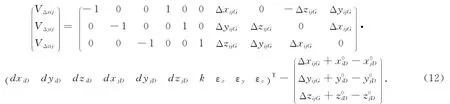
对于有m条基线向量，n个控制点（已知点也包含在内），l个已知点的GPS控制网来说，总的误差方程式写为

V＝BdX－L，权阵为P.（13）

经过上面的误差方程式推导，对于控制网中的已知点，方程中的坐标近似值和坐标改正数分别取已知坐标值的空间直角坐标和零值，对于控制网中的非已知点，坐标近似值代入该点的GPS坐标的平均值。

1.2 约束条件方程

GPS网的三维约束平差可以采用地面已知固定点坐标、固定大地方位角以及固定空间弦长等作为约束条件[1，4，6］。由于实际工程中往往地面已知固定点坐标条件容易获得，因此本文采用坐标条件进行三维约束平差。因为收集的已知坐标往往是国家或地方坐标系的大地坐标与大地高的形式，因此需要采用空间直角坐标与大地坐标的微分关系式[1］：

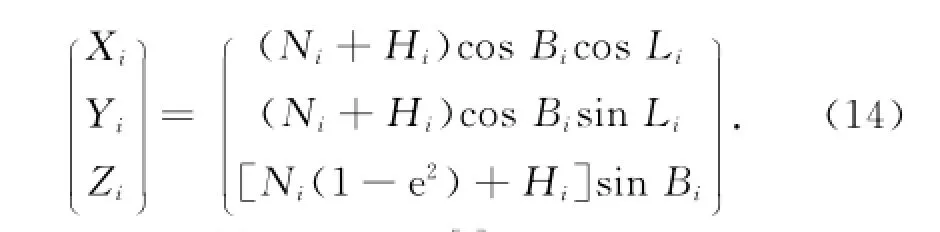
上式取微分并加以整理得[4］：

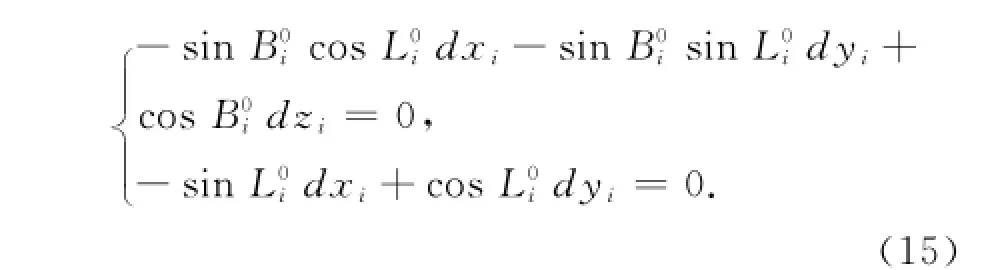
若该点的大地高已知，则另外有约束条件：

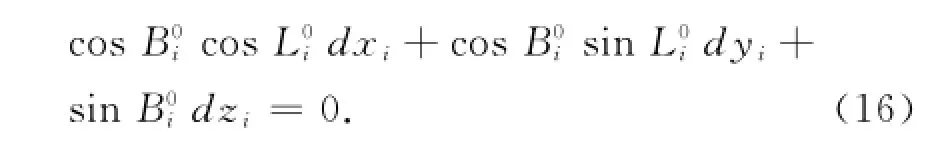
将该已知点约束条件写成矩阵的形式：

若GPS网中有l个已知控制点，则总的约束方程为

若采用已知点的空间直角坐标形式作为约束条件，则某已知点的约束条件方程为

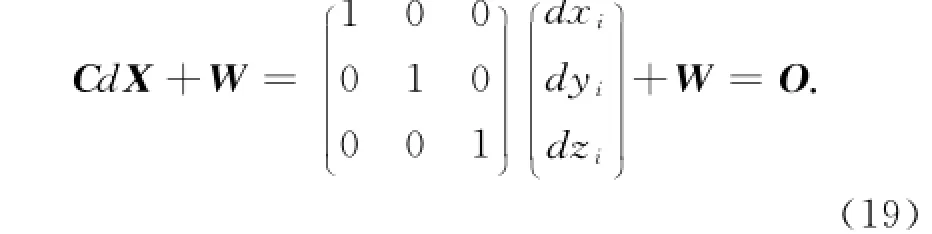
1.3 法方程的组成与解算[5－6］

采用GPS点的空间直角坐标为未知参数，理论上是附有条件的间接平差.

法方程的组成及解算实质是附有约束条件的间接平差方法[4］。误差方程为：

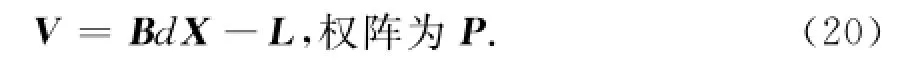
约束条件方程

组成法方程：

其中：

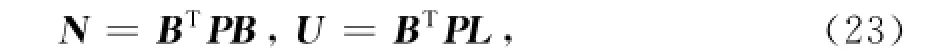
K为联系数，令则：

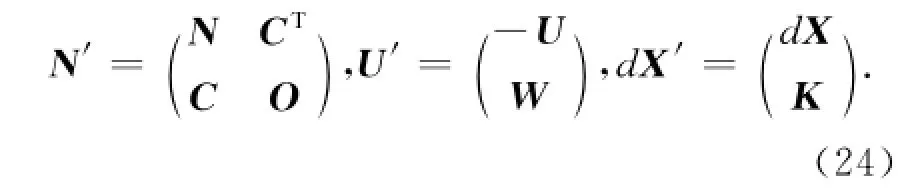
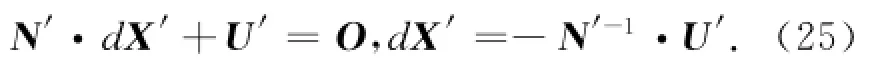
则根据式（25）可以解算出包含各未知点空间直角坐标改正数及转换参数在内的未知参数.

2 某工程GPS基线向量网三维约束平差案例分析

在某市周边收集到国家80坐标系D级GPS控制点3个，采用3台套中海达GPS进行了两个同步观测图形的静态观测，采用随机GPS后处理软件进行了基线解算，并分别进行了同步观测图形闭合差、异步图形闭合差等指标的检验，各项指标均符合《全球定位系统（GPS）测量规范》GB2009的要求。观测图形如图1所示，基线向量、方差－协方差阵如表1所示，待定点近似坐标表2所示，已知点坐标略。

图1 GPS网型分布图

表1 基线向量及其方差－协方差阵

表2 GPS待定点概略坐标

表3 Matlab与中海达HDS2003软件包平差结果比较

采用Matlab软件编写了相应的处理函数，对GPS基线向量、已知点坐标、待定点近似坐标进行读取，组成法方程系数矩阵、常数项矩阵，根据P＝·D－1（取0.005，D为基线向量的协方差阵）组成权阵，根据已知点的空间直角坐标组成约束条件方程系数阵，最终按照三维约束平差的法方程数学模型对待定点的空间直角坐标及坐标转换参数进行了解算.解算结果与中海达随机后处理软件HDS2003全球版进行了结果比较，如表3所示，二者的解算结果一致.

3 结束语

本文对GPS基线向量网的三维约束平差的数学模型进行了较为详细的推导，根据某实际工程案例采用Matlab软件平台进行了基线向量网的三维约束平差计算，给出了具体的计算案例，并对平差的结果与随机的商用GPS后处理软件计算的结果进行了对比，结果表明：采用Matlab进行基线向量网的约束平差有利于对约束平差数学模型的掌握与理解，利于某些特定应用的GPS数据处理人员对平差流程与结果提供更可靠的把握。

[1]徐绍铨，张华海，杨志强，等.GPS测量原理及应用[M］.武汉：武汉大学出版社，2008：162－168.

[2]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M］.武汉：武汉大学出版社，2009：146－157.

[3]白征东，刘大杰.GPS网3维平差软件的编程方法[J］.测绘通报，1999（12）：30－33.

[4]赵长胜，高刚毅，李广杰，等.GPS基线向量网在空间大地直角坐标系下的三维约束平差[J］.测绘工程，1998，7（4）：22－26.

[5]刘大杰，刘经南，刘国辉，等.GPS与地面测量数据的三维联合平差[J］.测绘学报，1994，23（1）：14－22.

[6]李征航，黄劲松.GPS测量与数据处理[M］.武汉：武汉大学出版社，2005：262－264.

[7]刘靖晔.分析几种常用的GPS数据处理软件[J］.全球定位系统，2013，38（3）：87－89.

[8]王 攀，刘 立.GAMIT在数据处理中若干问题探讨[J］.全球定位系统，2013，38（3）：84－86.

The Tri－Dimentional Constrainted Adjustment for GPS Baselines Vector Network Based on MATLAB Software Platform

WANG Zhongli1，GU Liudan1，2
（1.Jilin Jianzhu University，School of Geometrics and Prospecting Engineering，Changchun130118，China；2.Yunnan Design Institute Group，Kunming650228，China）

Nowdays，most GPS data processing personnel using commercial GPS software or sophisticated scientific software for baseline vector solution in control network.However because of surveying and mapping techicians’inadequate grasp about the mathematical model and underlying technologies in GPS software，there are some obstacles in high accuracy requirements of certain applications using GPS technology.After the three－dimensional mathematical models for baseline vector network is quoted and derived in detail，this thesis combined with a practical engineering cases and in the use of Matlab powerful matrix calculation function carried out 3Dconstrained adjustment calculations for GPS baseline vector network.Solver results obtained through Matlab compared to those obtained by HDS2003commercial software are consistant.This paper provide a reference and help for GPS data processors and related professional college students having a better understanding and mastery for GPS network adjustment.

GPS；Baseline vector network；tri－dimensional constraint adjustment；Matlab

P228.4

A

1008－9268（2015）01－0032－05

10.13442/j.gnss.1008－9268.2015.01.007

王忠礼（1978－），男，吉林长春人，讲师，博士生，主要从事GPS数据处理、空间分析与资源环境遥感等。

顾刘丹（1990－），男，云南曲靖人，助理工程师，目前主要从事工程测量工作。

2014－07－31

2012年度“吉林省高等学校大学生创新创业训练计划”项目；住房和城乡建设部2014年科学技术项目计划项目（编号：2014－K8－063）；2015年吉林省教育厅"十二五"科学技术研究规划项目

联系人：王忠礼E－mail：wangzhongli＠jlju.edu.cn