基于三次参数样条的等高线点加密算法

刘 旭，范磊磊，王宝水，闫玉强

（1.徐州市贾汪区国土资源局，江苏 徐州 221011；2.江阴市城市规划信息咨询中心，江苏 江阴 214433；3.苏州工业园区测绘地理信息有限公司，江苏 苏州 215027）

基于三次参数样条的等高线点加密算法

刘 旭1，范磊磊1，王宝水2，闫玉强3

（1.徐州市贾汪区国土资源局，江苏 徐州 221011；2.江阴市城市规划信息咨询中心，江苏 江阴 214433；3.苏州工业园区测绘地理信息有限公司，江苏 苏州 215027）

分析了DXF格式结构中各组码段与对应代码段的含义及关系特点，实现DXF文件的读写，并根据提取地形图中等高线的信息，利用VisualC++编写三次参数样条自动实现对等高线进行点加密算法。通过实例验证，该算法可保证等高线原始趋势不变，特别是出现大挠度等高线时，对等高线进行点加密，能保证地形图的准确性，提高工作效率。

Visual C++；三次参数样条；等高线；点加密

等高线是一种重要的反映区域地貌形态的基础数据[1,2]，工程中时常需要对等高线进行点加密，使其能更为细致地表示地貌特征[3]。基于VisualC++平台对DXF格式文件进行读写，根据等高线上已知的（x，y）信息，利用三次参数样条对等高线上的点进行加密，能有很好的效果。

1 DXF文件及三次参数样条差值

1.1 DXF文件的结构

从结构上，DXF文件[3]是由一系列的组构成的。组作为DXF文件中的最小单元，与一行整数型组码及连续的下一行组值（对组码的描述说明）构成。

DXF文件由6节构成[4]，其中实体节包含图形中所有的实体（如多段线、点、构造线等）信息，如点的高程、坐标、所在图层、颜色等，以组码2及对应组值ENTITIES标志开始。

等高线是以多段线的方式表现的，在DXF格式文件中多段线以组码0及对应组值LWPOLYLINE，主要实体数据[4]见表1。

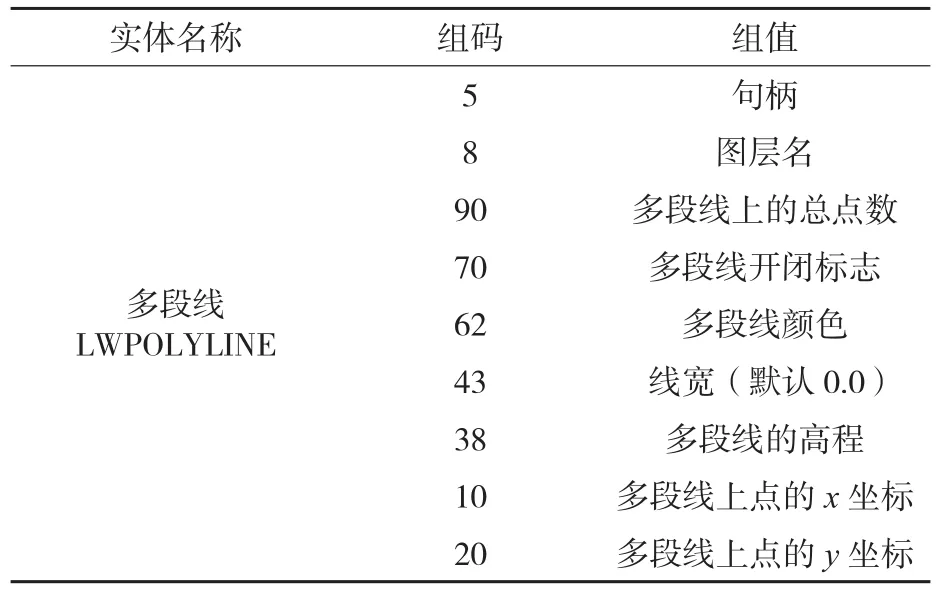
表1 多段线的实体数据表

1.2 三次参数样条插值

目前常用的曲线插值方法有拉格朗日插值法、分段低次插值法、张力样条插值法、样条插值法等[4]。其中以样条插值中的三次样条插值、三次参数样条插值最为常用[5]。

三次样条插值在曲线小挠度的情况下满足要求，当挠度过大时，不能很好地控制曲线的弯曲度，样条曲线与实际曲线挠度偏差较大，使得曲线失真[6]。

1.2.1 三次参数样条函数

三次参数样条曲线函数是以曲线的弦长li作为参数的函数，表达形式一般为：空间曲线上的节点为pti（xi，yi，zi）（i=0，1，…，n）。若函数S（x）是该空间曲线的函数，每个区间[pti，pti+1]，（i=0，1，…，n-1）是三次多项式的形式：

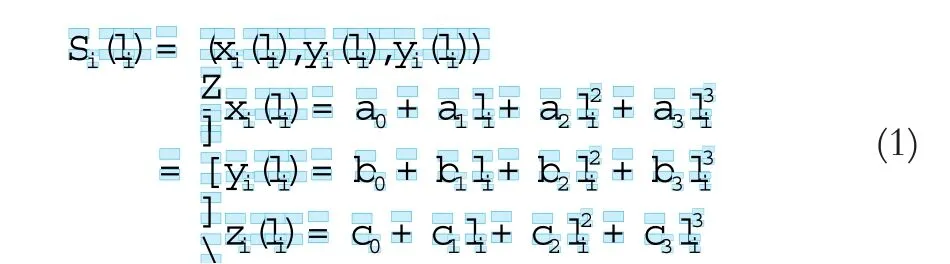
式中，l∊[0，Li]。Li为第i段的弦长：

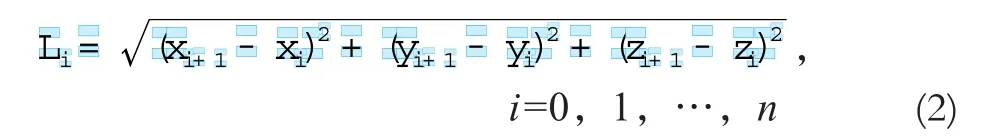
且在节点处满足连续性条件：

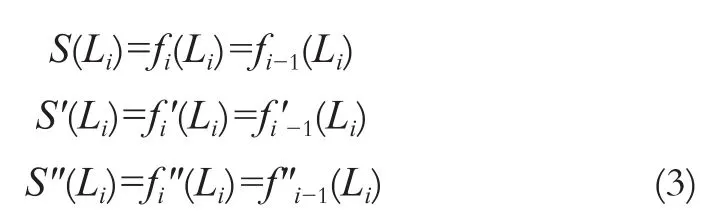
由式（1）～（3）可知，共有4n-2个条件。还需2个条件，在区间边界点pt0和ptn处各增加1个条件（边界条件）。常用的边界条件有3种：夹持端、自由端、抛物端。

1.2.2 构造三次参数样条函数

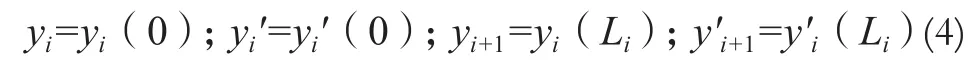
可得：

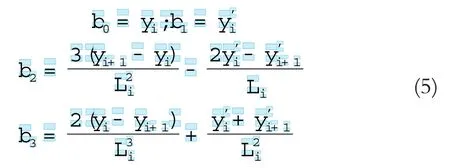
将式（5）代入式（1），由样条曲线二阶导数连续可得：

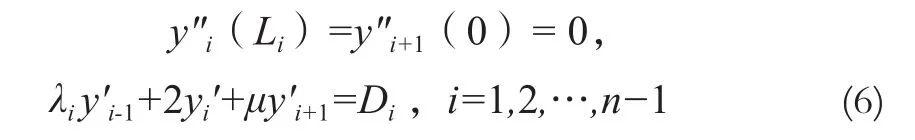
其中，

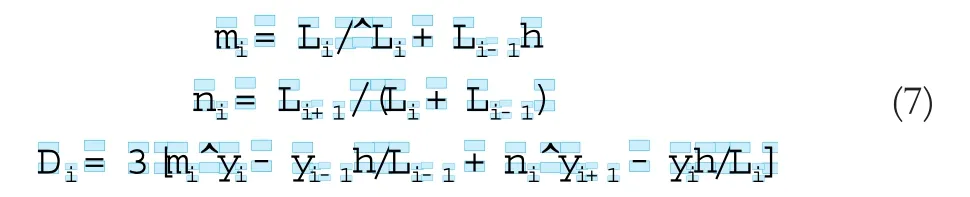
由上式可得到4n-2个方程，根据边界条件可增加2个方程，见表2。则式（6）写为矩阵形式BY'=D：

表2 三次参数样条曲线的边界条件

代入式（1），得到曲线方程Si（li）中yi（li）的方程。同理，求得曲线方程Si（li）中的xi（li）及zi（li）。

2 算法设计

2.1 数据格式

由于等高线在CAD中以多段线的形式体现，对应表1，以结构体typedef struct的形式声明等高线类型。

等高线上的点（x，y）类型：

typedef struct{double x; //点的x值 double y; //点的y值} BPoint;

等高线类型：

typedef struct{CString layer; //图层名 int color; //颜色值 int bz; // 0开曲线，1闭曲线

int ds; //等高线上的点数 double h;//等高线的高程 BPoint *pt; //等高线上的点 }Pline;

定义变量Pline addpl，表示一次读取的等高线。由于在读取DXF文件时等高线的总条数不可知，在doc类中以动态数组Carray[7]的形式定义类型为Pline的全局变量CArray＜Pline,Pline&＞m_Pline，为了便于读写加密等函数对其赋值修改等。将每次获取的等高线添加到数组m_Pline中，m_Pline.Add(addpl)。

以结构体的形式声明三次参数样条曲线上节点类型：

typedef struct{ double l; double y; }SPoint;

其中，第i条等高线对应参数样条曲线上节点总数为int ds=m_Pline.GetAt(i).ds。

定义每条进行三次参数样条插值曲线的节点动态数组Spoint *spl; spl=new Spoint [ds],并根据对应等高线进行赋值。

2.2 等高线的读取

由于在DXF文件中每个组信息中组码和组值各占一行，故每次读取两行。根据不同组码所对应的组值信息不同，可用if…else if…语句对add_pt中的变量赋值。

定义CString型变量cs,data，并将读入的字符串赋值给cs，data。

组码定义为int型变量code，并将读入的第一行赋值给code，data包含组值信息。

1）等高线对应的多段线是一种实体，定义开始（结束）读取实体节的标志，并初始化，根据组结构，判断是否开始（结束）读取实体节。

2）进入实体节，定义开始（结束）读取多段线的标志，并初始化，根据组结构判断是否读取多段线。

3）定义中间变量，根据表1多段线的实体数据表中组的对应格式，从data中赋值。

2.3 构造三次参数样条函数矩阵

定义Pline pl=m_Pline.GetAt(i)，获取第i条等高线的信息。可确定总点数int n=pl.ds即B、D矩阵的大小为n×n、n×1。

三次参数样条节点数组Spoint *spt=new Spoint[n];将pl.pt赋值给spl。由于多段线上各处高程hi相等，定义变量double L[n-1],U[n],Lmd[n-1],D[n][1]。由式（2）、式（7），对L、U、Led、D进行普通情况下的赋值。

对于不同的边界条件（见表2），λn，μ1，D1，Dn不同，定义变量 int choice，switch…case…语句，确定边界条件，伪代码形式见图1。确定矩阵B及D，然后求得矩阵Y'。

图1 选取边界条件伪代码图

2.4 点自动加密算法设计

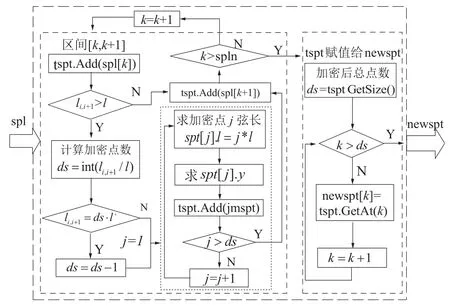
图2 自动加密点算法流程图

2.5 算法实现

通过消息映射的方式，在菜单栏中映射doc类函数：

void OnReadDxfFile(); //读取DXF文件

void OnPointEncryption(); //等高线上点加密

void OnWriteDxfFile();

//储存等高线点加密后DXF文件

将加密算法封装到CCubicSpline类中。其中包含：

class CCubicSpline : public CObject{

public : void EncryptPline(Pline pl,Pline &newpl); //对等高线上的点加密

private: void PraCubSpline(SPoint *spl,int n,SPoint *spt,int ptn); //三次参数样条曲线

double **InvMatrixl(double **A,int n); //高斯列主元消去法求逆矩阵

double **MulMatrix(double**A,double**B,int m,int n,int k); //矩阵相乘 }

算法的实现流程：

1）读取DXF格式文件，并将提取的等高线信息赋值给m_Pline。

2）对等高线pl上的点进行加密。将等高线点赋值给三次参数样条节点并进行加密；差值后三次参数样条节点赋值到等高线中，并通过m_Pline.SetAt（i，pl）赋值到等高线动态数组中。

3）以DXF格式写出文件。

3 算法验证

三次样条曲线在小挠度情况下，效果较好，当挠度过大时，样条曲线与实际曲线有很大的偏差。而三次参数样条可以很好地解决大挠度问题，见图3。

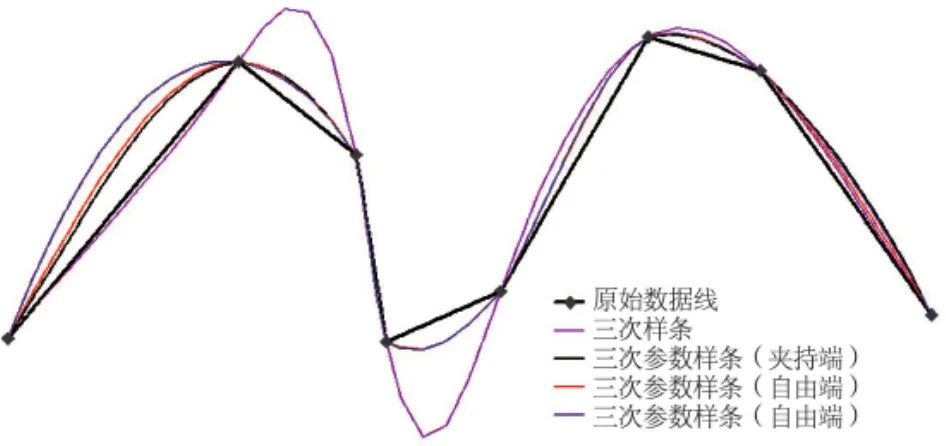
图3 三次样条与三次参数样条对比图

从整体趋势分析，三次参数样条在3种边界条件下，边界条件选取夹持端效果较好。故在对等高线进行点加密时采用夹持端的方法进行加密。加密后的效果见图4。

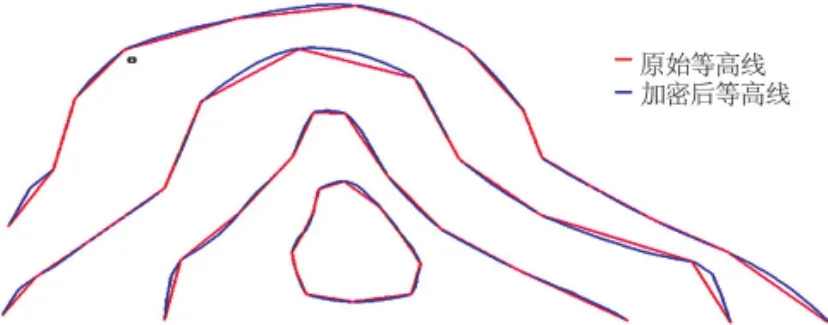
图4 等高线上点加密效果图

4 结 语

本文算法在不破坏原始等高线趋势的情况下利用三次参数样条对等高线进行点加密，生成的等高线有较高的光滑性。较三次样条插值精度更高，避免了大挠度情况下出现失真情况，能准确地反映实地地形特征，大大缩短工作时间，且该算法程序基于Visual C++编写，实现简单，可代替传统的手工方法。

[1] 陈丹.地形图等高线自动识别与提取中的若干方法研究[D].武汉:武汉大学,2004

[2] 夏春林,王雪,叶长青.等高线自动识别方法的研究[J].矿山测量,2007(1):32-34

[3] 郭庆胜,于江佩,徐峥,等.等高线图形综合策略的研究[J].测绘信息与工程,2005,30(6):16-18

[4] 刘传亮,陆建德.AutoCAD DXF文件格式与二次开发图形软件编程[J].微机发展,2004,14(9):101-104

[5] 郭朝勇. AutoCAD R14二次开发技术[M].北京:清华大学出版社,1999

[6] 李庆扬,王能超,易大义,等.数值分析[M].北京:清华大学出版社,2006

[7] 陈凤祥,李汪根.C++动态数组的实现与重用[J].计算机技术与发展,2010(2):79-82

P208

B

1672-4623（2015）04-0148-03

10.3969/j.issn.1672-4623.2015.04.053

刘旭，工程师，主要从事工程测量相关工作。

2013-09-17。