通用关联规则挖掘框架的设计与实现

董 林，舒 红

（1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079）

通用关联规则挖掘框架的设计与实现

董 林1，舒 红1

（1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079）

对适用于多种数据类型的关联规则挖掘框架进行了研究。从概率论出发讨论了支持度计算问题，提出利用有限测度计算项集支持度的方法，分析了Apriori性质的本质，提出通用关联规则挖掘算法的设计思路。在此基础上，设计并实现了通用关联规则挖掘框架，使用该框架进行了事务、空间和时空数据的挖掘实验，验证了其可行性、通用性及正确性。

关联规则；空间关联规则；时空关联规则；支持度；测度；通用框架

关联规则挖掘是一种用于分析事物和现象之间内在联系的数据挖掘方法，挖掘的对象可以是数据库或数据仓库中的事务数据[1]，也可以是空间、时态或时空数据[2-4]，随着研究与应用的发展，更多种类的数据将成为关联规则挖掘的对象。多样化的数据带来了对多样化挖掘算法的需求，研究适用于多种数据类型的算法框架对加速新算法的设计与实现有重要意义。为此，提出一种通用关联规则挖掘框架GARMF（general association rule mining framework）。

1 理论基础

要设计适用于多种数据类型的通用挖掘框架，必须解决2个问题：①将针对不同数据类型的项集支持度计算方法纳入统一框架；②找出通用的关联规则挖掘算法。关联规则挖掘是从数据中提取频繁模式（频繁项集和关联规则）的过程，模式频繁与否是根据其支持度（即对应事件发生的概率）进行判断的，因此支持度计算是关联规则挖掘中最重要的操作。同时，关联规则挖掘是一种复杂度较高的计算。为了确保挖掘效率，必须选用合理的挖掘算法。以概率论为基础，GARMF利用有限测度之比以及经典Apriori算法的框架来解决这2个问题，下面对其原理进行介绍。

1.1 基本概念

定义1 σ域。由非空集合X的一些子集组成的集合称为X上的集合系。满足以下3个条件的集合系F称为σ域（也称作σ代数）：

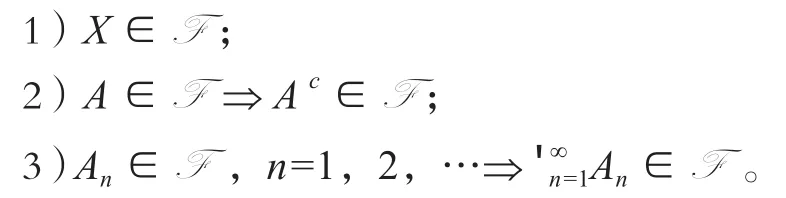
定义2 测度。设E是X上的集合系且∅∈E，如果E 上的非负集函数μ有可列可加性且有μ（∅）=0，则称之为E 上的（σ可加）测度（measure）。

称（X，F ，μ）为测度空间，其中X是一个给定的非空集合，F 是X上的σ域，μ是F 上的测度。

定义3 概率。对于测度空间（X，F ，P），如果P（X）=1，则可以称之为概率空间，称P为概率测度，称集合A∈F 为事件A，称P（A）为事件A发生的概率。

定义4 项集。对于有限集I={i1，i2，…，in}，称其中每个元素为一个项，称2I中的元素为项集，称包含n个项的项集为n-项集。

称一个非空点集Ω为基本事件空间。给定一个映射f：I ↦2Ω，对于任意项A∈I，称f （i）为i的对应事件。例如，对于事务数据来说，基本事件空间Ω是用所有事务记录的集合，一个项的对应事件即其对应字段取真值的事务记录的集合。

对任意项集A={a1，a2，…，am}（A⊂ I），称为其对应事件，称P（Ae）为其支持度。

定义5 关联规则。用 A，B⊂ I（A ( B=∅）组成的蕴含式A⇒B来表述条件概率P（Be|Ae），称这个蕴含式为关联规则，称这个条件概率为该规则的置信度。称A ' B为规则对应的项集，那么Be(Ae就是规则对应的事件，P（Be(Ae）就是规则的支持度。

1.2 支持度是有限测度之比

基于事务表的关联规则挖掘算法大多是利用古典概型的概率公式计算支持度的。对于一个由m条事务记录组成的事务表，如果满足某项集的事务有m条，则该项集的支持度为m/n[2]。这是目前占主导地位的支持度计算方法。一些文献采取了基于几何概型的计算方法[6-9]，例如Estivill-Castro[7]利用面积之比来计算支持度：假设满足某项集的区域面积为a，研究区域总面积为A，则该项集的支持度为a/A。虽然两种方法有区别，但本质上又是相同的：计算的都是项集对应事件的概率，并且这个概率都是用一个除式得到的。基于古典概型的计算方法使用的是总事务数n和满足项集的事务数m，它们的本质是计数测度，这是一个有限测度；在基于几何概型的计算方法中，研究区域总面积A和满足某项集的区域的面积a，本质上是面积测度，同样是有限测度。显然，这两种方法实际上是用有限测度的比值来计算项集的支持度。对于基本事件空间Ω，假设存在定义于2Ω上的有限测度m，则任意项集A的支持度（即其对应事件Ae∈2Ω的概率，）可以用如下公式计算：

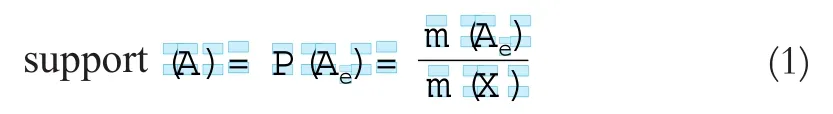
m（Ω）/m（Ω）=1，由此可知：

1）m/m（Ω）是一个定义在2Ω上的概率测度；

2）m（Ae）/m（Ω）可称作事件Ae的概率；

3）m（Ae）/m（Ω）作为A的支持度是合理的。式中，m（Ω）为数据总量； m（Ae）为项集A的支持度计数；项集的支持度等于其支持度计数与数据总量之比。对于任意一类描述事件域内一组事件的数据，只要能找到可计算的有限测度m，就可对其进行关联规则挖掘。

1.3 Apriori性质的本质

绝大多数关联规则挖掘算法会利用Apriori性质来提高挖掘效率。所谓Apriori性质，即任意频繁项集的子集必然是频繁的，或者说，任意项集的支持度不低于其超集的支持度。从概率论的角度来看，对于任意项集A、B（A，B⊂ I），如果A⊂ B则Be⊂ Ae，那么对于任意概率测度P都有P（Be） ≤ P（Ae）。显然，Apriori性质的本质是概率测度的非负性和可列可加性，是支持度固有的数学性质，而不是由事务数据的逻辑或存储结构带来的。因此，基于Apriori性质的经典Apriori算法[10]虽然是针对事务数据设计的，但将具体的支持度计算操作（即遍历事务表）抽象为一般的支持度计算操作，就可以得到一个通用于各种数据类型的关联规则挖掘算法。

2 框架的设计与实现

2.1 GARMF的架构

关联规则挖掘主要涉及数据、算法和挖掘结果这3类要素，GARMF将它们抽象为数据类、通用挖掘算法类和挖掘结果类，如图1所示。

图1 GARMF架构图

1）数据类。数据类是对可以用于关联规则挖掘的数据的抽象。不论挖掘对象为何种类型的数据，不论采用何种挖掘算法，用于关联规则挖掘的数据总是描述项的对应事件的数据，项集的支持度也总是利用有限测度m来计算。

2）通用挖掘算法类。现有的关联规则挖掘算法大都是针对某些具体的数据类型设计的，集成了访问数据计算支持度的操作。在GARMF框架中，这一操作则由数据类负责，这使得挖掘算法与具体的数据类型相对独立，具有较强的通用性。

3）挖掘结果类。挖掘结果类的功能是存储频繁项集和关联规则。之所以还要保存频繁项集是因为一些应用所需的是频繁项集，并且很多评价方法和增量挖掘算法要用到频繁项集（及其支持度）。

2.2 GARMF的实现

本文将GARMF框架实现了一个Java类库（称作GARMF类库），该类库核心的3个类如图2所示。

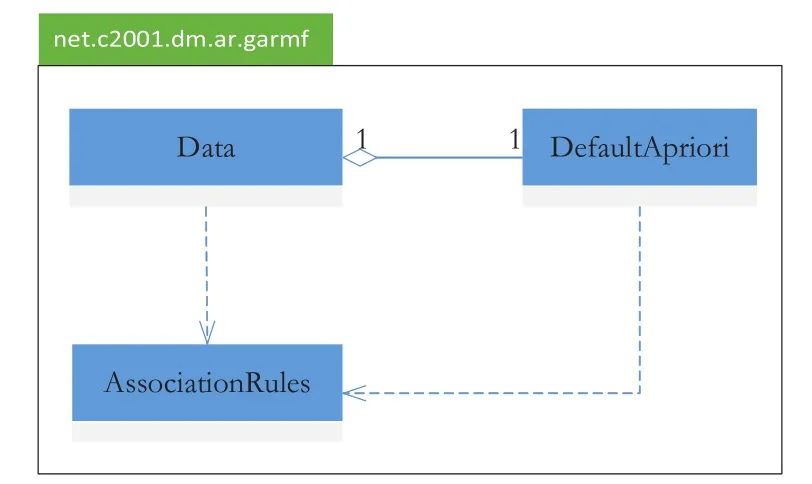
图2 GARMF类库的核心类

1）数据类（Data）。使用抽象类Data来表述可用于关联规则挖掘的数据（如图3所示）。Data类最重要的3个属性是miner、recordCount和items，分别为关联规则挖掘算法、数据总量以及项集到对应数据的映射；最重要的2个方法是mine和getSupportCount，即进行关联规则挖掘和获取指定项集的支持度计数。需要指出的是，虽然数据总量和支持度计数实际上是用同一个有限测度求出的，但对于一组数据其总量是恒定的，只需要求一次，而要计算支持度计数的项集则有很多个，因此数据总量recordCount被作为属性来处理，getSupportCount则是作为方法。

2）挖掘结果（AssociationRules）。使用AssociationRules类来存储挖掘结果，包括挖掘所使用的最小支持度和置信度阈值、挖掘得到的频繁项集和关联规则。挖掘阈值对挖掘结果的影响很大，并且是进行增量式挖掘的必要信息。

3）通用挖掘算法（DefaultApriori）。将Apriori算法[10]的核心抽取出来，得到了通用关联规则挖掘算法DefaultApriori。该算法的输入为Data对象，输出为AssociationRules对象，与具体的数据类型无关。需要指出，该算法输入的Data对象负责数据总量及支持度的计算。Data类是一个抽象类，应当根据具体的数据类型创建其实例，主要工作就是实现用于计算数据总量和支持度计数的有限测度。

为了便于使用，还实现了一些用于挖掘结果查看和持久化的类，并针对一些常用数据类型设计了Data的子类（部分见图3），包括基于文件的/基于数据库的/加权/模糊事务数据、空间数据（矢量/栅格）以及时空数据（快照序列）。这些虽然不是核心类，但对GARMF类库的实用性有重要意义。

图3 GARMF类库中的数据类

3 实验验证

用GARMF对事务数据、栅格数据、矢量数据以及快照序列数据进行关联规则挖掘实验以检验其可行性与正确性。为了便于对比分析，本文使用与文献[11]相同的实验数据。该类库以及实验数据均可在作者网站http://www.c2001.net/GARMF.html下载（含API文档，完成软件著作权登记后将开放全部开源代码）。

3.1 数据准备

本文实验所使用的是美国地质调查局（USGS）覆被变化趋势项目网站（http://landcovertrends.usgs.gov）上提供的威拉米特河谷生态区（Willamette Valley Ecoregion）第3号样本区（图4）的覆被序列数据，由5幅大小为167×167像素、分辨率为60 m的栅格格式的覆被分类图组成，分别对应于该样本区1972、1979、1985、1992和2000年的覆被状态。数据涉及的覆被类型及它们在各个时期的状况见表1。

图4 威拉米特谷生态区第3号样本区的地理位置[11]

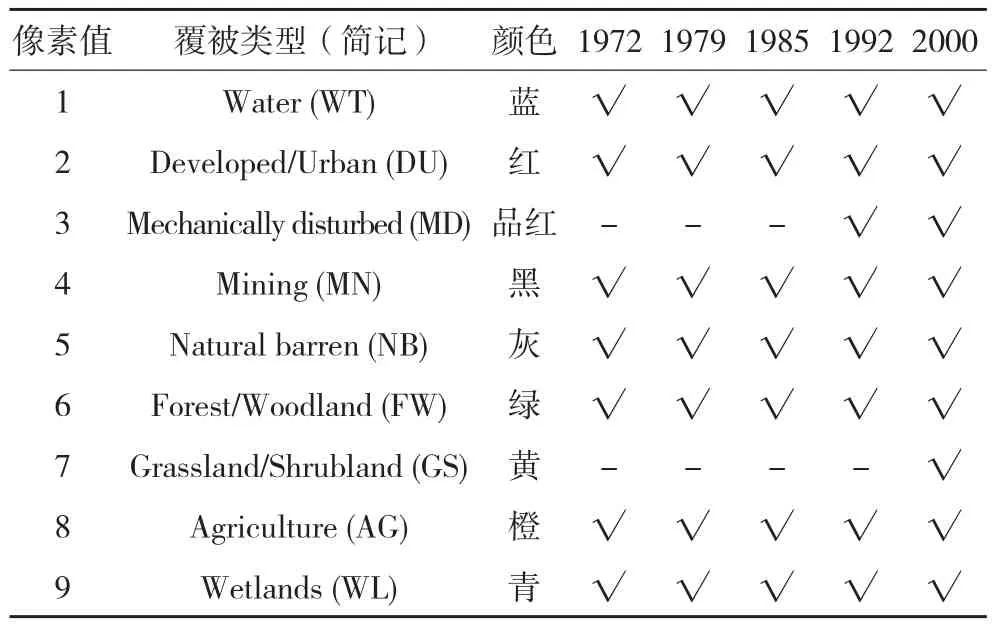
表1 数据涉及的覆被类型及出现情况

要进行关联规则挖掘，必须先选定项的集合。本文以时间与覆被类型的组合作为项，例如“1972年农业用地”（简记为1972AG）。如表1所示，实验数据中实际存在的组合共38种（用对号标出），因此共有38 个项。接下来，分别将这组数据转换为事务数据、矢量数据、栅格数据以及快照序列数据以进行挖掘实验。

1）事务表。以一个像素位置作为一个事务单元，研究区域可划分为27 889个事务单元，因此实验数据可以转换为一个具有38个布尔型字段（对应于38个项）、27 889条记录的事务表，表中每条记录存储一个像素位置各年份的覆被状态。例如，如果一个像素位置在1972、1979、1985、1992和2000年的覆被类型分别为AG、AG、AG、DU、DU，则相应的事务记录为{ 1972AG, 1979AG, 1985AG, 1992DU, 2000DU}（即这些字段取值为真，其余字段取值为假）。

2）栅格数据。依照像素值对覆被序列数据进行分割，得到一组由38个栅格图层组成的栅格数据，每个图层对应一项，表示一种覆被在某一年份的空间分布情况。例如在1972AG对应图层中，如果一个像素取值为1，则表示该位置在1972年覆被类型为农业用地。

3）矢量数据。对上一步骤所得到的栅格数据中每一个图层进行矢量化，所得到的矢量图层的集合就是一组可用于关联规则挖掘的矢量数据（共含38个多边形图层）。

4）快照序列数据。将样本区5种主要覆被类型（AG、DU、FW、WL和WT）保存为5个栅格快照序列，并生成了表述与它们在空间上邻近/远离（例如Near_AG和Far_AG）、由它们转入/转出（例如Trans_From_AG和Trans_To_AG）的时空区域的栅格快照序列，并将1972、1979、1985、1992和2000这5个年份用栅格快照序列来表述，得到一组由31个快照序列组成的快照序列数据。

3.2 实验与分析

在实验中用于挖掘的事务数据、栅格数据和矢量数据源于同一组覆被数据，二者表述的项相同，选取相同的支持度阈值，利用GARMF对其进行关联规则挖掘所得结果应当完全一致。因此，可以将挖掘结果的一致性作为其正确性的判据。这些数据与文献[11]中挖掘算法的输入数据相同，因此还可以与该文献中实验结果（使用的不是GARMF）进行对比。

挖掘事务数据、栅格数据和矢量数据所使用的最小支持度阈值参照文献[11]，设为10-7，得到3组频繁项集，它们的数量、内容和支持度完全一致（因此根据频繁项集生成的关联规则也相同），并且与文献 [11]中的挖掘结果相符。挖掘得到的频繁项集共有510个，包括38个1-项集、140个2-项集、189个3-项集、116个4-项集和27个5-项集。表2列出了支持度最高的5个频繁5-项集，这些项集中都只包含对应于同种覆被类型的项，且其支持度之和为93.858%，由此可知该样本区从1972年到2000年覆被类型基本维持不变。

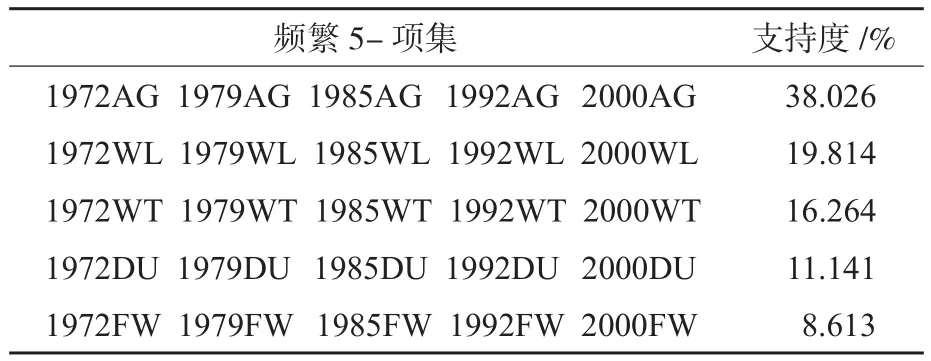
表2 支持度最高的频繁5-项集

取10-7为最小支持度阈值、0.75为最小置信度阈值，对快照序列数据进行挖掘，共得到24 505个频繁项集和54 045条关联规则。其中，2到9-项集共24 474个，9-项集共有44个。9-项集中支持度大于0.1%的只有{AG, Near_DU, Far_WT, Far_WL, Far_FW, Trans_From_AG, Trans_To_DU, change, 1985}（0.11%）。由该项集可以得知，有一些1985年邻近建筑用地的农田到1992年会变为建筑用地。由于该项集包含时间项1985，可以直接用GIS对各项对应于1985年的快照图层进行求交得到该项集对应的栅格快照序列中唯一一个非空图层。该图层共包含147个取值为1的像素，而研究区域总共有167×167×5=139 445个像素，其比例为0.11%，与挖掘结果一致。

显然，GARMF类库能够对事务数据、栅格数据、矢量数据和时空数据（快照序列）进行关联规则挖掘并得到可靠的结果，这表明GARMF框架不仅是正确的理论框架，还是切实可行的。

4 结 语

本文设计并实现了GARMF框架，旨在降低挖掘新的数据类型的难度。对于任意一类可用于关联规则挖掘的数据，只需要找出数据总量和支持度计算方法（即有限测度m），就可以利用该框架对其进行挖掘。但GARMF主要关注关联规则挖掘问题，挖掘结果（即频繁项集和关联规则）的评价、筛选及可视化方法还有待进一步研究与实现。

[1] Agrawal R, Imielinski T, Swami A. Mining Association Rules between Sets of Items in Large Databases[C].1993 ACM International Conference on Management of Data (SIGMOD93),1993

[2] Han J, Kamber M, Pel J. Data Mining:Concepts and Techniques[M]. Morgan Kaufmann, 2011

[3] Koperskik, Han J. Discovery of Spatial Association Rules in Geographic Information Databases[C].London: Springer Berlin Heidelberg, 1995

[4] 李光强, 邓敏, 张维玲，等. 利用事件影响域挖掘时空关联规则[J]. 遥感学报, 2010, 14(3): 468-481

[5] 程士宏. 测度论与概率论基础[M]. 北京: 北京大学出版社, 2004

[6] 董林, 舒红, 牛宵. 利用叠置分析和面积计算实现空间关联规则挖掘[J]. 武汉大学学报:信息科学版, 2013, 38(1): 95-99

[7] Estivill-Castro V, Lee I. Data Mining Techniques for Autonomous Exploration of Large Volumes of Georeferenced Crime Data[C]. 6th International Conference on Geocomputation,2001

[8] Sha Z, Li X. Mining Local Association Patterns from Spatial Dataset[C].Fuzzy Systems and Knowledge Discovery (FSKD), 2010

[9] 李中元. 基于空间缓冲矩阵的空间关联知识提取与表达[D].武汉：武汉大学, 2012

[10] Agrawal R, Srikant R. Fast Algorithms for Mining Association Rules[C].20th International Conference on Very Large Databases(VLDB94),1994

[11] 董林, 舒红, 李莎. 直接从空间数据中挖掘频繁模式[J]. 计算机应用研究, 2013, 30(8): 2 330-2 333

P208

B

1672-4623（2015）04-0068-04

10.3969/j.issn.1672-4623.2015.04.025

董林，博士，研究方向为空间数据挖掘。

2014-07-23。

项目来源：国家自然科学基金资助项目（41171313）;苏州市科技计划2013年应用基础研究计划资助项目（SYG201319）。