超高分子量聚乙烯纤维增强层合厚板抗高速钝头弹侵彻的理论模型

陈长海，徐文献，朱锡，侯海量

1 海军工程大学舰船工程系，湖北武汉430033

2 海军湛江地区装备修理监修室，广东湛江524005

0 引 言

超高分子量聚乙烯（UHMWPE）纤维由于具有防弹性能好及密度低等优点，近年来在防护领域得到了广泛的关注。关于超高分子量聚乙烯纤维增强塑料（UFRP）层合板的抗侵彻机理问题，国内外的学者们开展了大量的试验研究［1-6］，并给出了在一定速度范围内UFRP 层合板的弹道吸能［1］或弹道极限［5-6］随靶板面密度变化的经验关系式。然而，这些经验关系式针对的都是特定的弹靶系统，具有一定的局限性。

受层合板纤维的韧脆特性以及靶板厚薄等因素的影响，致使不同类型层合板在抗侵彻过程中的破坏模式及吸能机理差异较大，因而很难建立适合不同类型层合板的理论模型。早期层合板的抗侵彻理论模型大多是基于单一的变形模式及特定的弹靶系统，主要分为针对脆性中厚层合板［7-9］的理论模型和针对韧性层合薄板［10-12］的理论模型2 大类。梅志远等［13］基于纤维增强复合材料（FRC）层合板抗高速侵彻的变形和破坏模式分析，提出了两阶段理想侵彻模型，并指出该模型适用于不同类型的FRC 层合板。然而，从与该文试验结果的比较可看出，文献［13］中的模型对于韧性FRC 层合板的适用性要好于脆性FRC 层合板。

在对大量UFRP 抗侵彻试验研究结果［1-6］进行分析的基础上，陈长海等［14］提出了钝头弹高速侵彻中厚UFRP 层合板的三阶段理论模型，理论计算值与相关文献试验结果吻合较好。但文献［14］中的模型对于UFRP 层合厚板抗高速侵彻的情形不能进行很好的计算和预测，例如，不能计算UFRP 层合厚板未穿透情形下的弹体总侵彻深度（depths of penetration，DOP）以及存在层合厚板弹道极限预测值偏高等问题。基于此，本文将结合UFRP 层合厚板抗高速侵彻的特点，通过改进开坑镦粗阶段的计算方法和拉伸变形阶段的计算过程，建立UFRP 层合厚板抗钝头弹高速侵彻的理论模型，然后利用该模型计算弹体侵彻深度和层合厚板的弹道极限速度，并与相关文献试验结果进行比较，以验证模型的实用性和有效性。

1 侵彻过程分析

相关的试验研究结果表明［1-6］，UFRP 层合厚板在抗高速侵彻的过程中，其迎弹面会产生纤维熔断，厚度方向会呈现剪切和拉伸变形这2 种失效模式。另外，弹体在侵彻的过程中其头部会出现明显的镦粗变形。因此，将UFRP 层合厚板的抗侵彻过程分为3 个阶段，如图1 所示。图中Hp为变形锥的高度。

开坑镦粗阶段是UFRP 层合厚板抗高速侵彻的第1 个阶段。在开坑镦粗阶段，层合板迎弹面侵彻区近似呈现流体动力状态，熔断纤维及碎裂基体由于弹体的挤压作用会向抗力最小的方向，即反向飞溅喷出，从而出现试验中的反向喷射现象。当弹体速度与接触界面的运动速度一致时，开坑镦粗阶段结束（图1（a））。开坑镦粗阶段结束后，UFRP 层合厚板即进入剪切压缩阶段（图1（b）），而剪切压缩阶段结束后，层合厚板则进入拉伸变形阶段（图1（c））。剪切压缩阶段和拉伸变形阶段的UFRP 层合厚板受力状态与中厚板［14］相同。

2 各阶段吸能计算

2.1 开坑镦粗阶段

在文献［14］的理论模型中，压缩镦粗阶段（即本文的开坑镦粗阶段）的侵彻深度取的是层合板总厚度的0.1 倍，这是基于试验结果得到的，即在试验结果的基础上，通过对相同厚度层合板在不同侵彻速度下各次试验结果取平均值而得到。虽然该压缩镦粗阶段侵彻深度的取法具有一定的合理性，也在一定程度上体现了弹体速度以及弹靶材料的影响，但随着层合板厚度的增加，穿透层合板所需的弹丸初速（即层合板的弹道极限）也会相应提高。因此在一定穿透速度范围内，随着层合板厚度的增加，压缩镦粗阶段的侵彻深度会相应增大，从而表现出侵彻深度随层合板厚度的变化现象，文献［5-6］的试验结果也证实了这一点。由此可见，文献［14］中压缩镦粗阶段侵彻深度的取法存在一定的局限性，不能很好地体现弹丸初速侵彻速度的影响。为进一步提高理论模型的适用性和普适性，本文对UFRP 层合厚板抗钝头弹高速侵彻的初期，即开坑镦粗阶段的计算方法进行了改进，以期能对UFRP 层合厚板抗钝头弹高速侵彻的情形进行合理、准确的计算和预测。

在开坑镦粗阶段，UFRP 层合厚板迎弹面会出现纤维熔断和基体碎裂现象，同时弹丸头部会产生一定程度的镦粗变形，且镦粗变形程度会随弹体侵彻速度的增大而变大。假设弹体的镦粗变形仅发生在开坑镦粗阶段，开坑镦粗阶段结束后，认为弹体头部不再发生镦粗变形。对于类似于金属靶板的弹体镦粗问题，可将层合板看做可变形的靶板，弹体高速侵彻可变形靶板的过程如图2 所示。图中：l 和lp分别为弹体刚性区（未变形区）和塑性区（变形区）的长度；h 为弹体侵入靶板的深度；u 为塑性界面向左传播的速度；v 为弹体刚性区的运动速度（即弹体的运动速度）；vc为弹靶接触界面的运动速度；A0为未变形区截面积；A为变形区截面积。

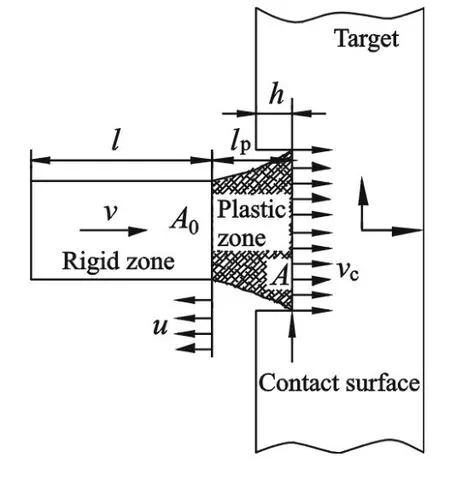
图2 弹体撞击可变形靶板示意图Fig.2 Schematic of projectile impacting on deformable target

对于弹体，根据动量冲量守恒，可得dt 时间内弹体动量转化为塑性区中压缩冲量的增量I 为

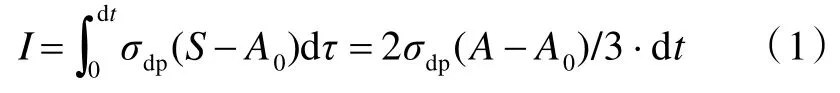
式中，S 为截面积的积分符号。

对于弹靶接触界面，根据动量冲量守恒定律，有

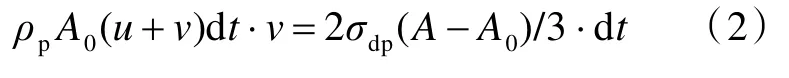
式中，ρp和σdp分别为弹体的质量密度与动屈服强度。

通过推导、代换、整理后，可得弹体镦粗后的直径d1和截面面积A1分别为：

式中，e=λ+1+(λ2+2λ)0.5，其中v0为弹体初速，K=1+(ρpcp)/(ρtct)，而ρt为靶板的质量密度，cp和ct分别为压缩应力波在弹体与靶板中的传播速度。

设弹靶接触界面的接触应力为σj，弹体由于接触应力作用而引起的向左后退的速度为v1，靶体由于接触应力作用而引起的向右运动的速度为v2（即接触界面的运动速度vc），则有vc=v2=v0-v1。根据撞击时的动量冲量守恒定律，可得弹靶接触界面的运动速度为［15］

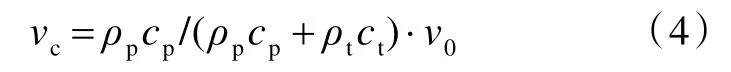
开坑镦粗阶段结束时，弹体速度v1=vc。因此，该阶段的总耗能W1为

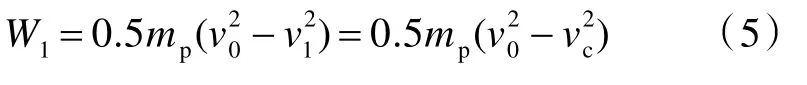
式中，mp为弹体质量。

在开坑镦粗阶段，弹体的侵彻时间为t1，因而可得开坑镦粗阶段弹体的侵彻深度h1为

2.2 剪切压缩阶段

剪切压缩阶段分初始压缩波的传播和反射拉伸波的反向传播2 个子阶段。

在初始压缩波传播子阶段，层合板的压缩耗能Wc21和剪切耗能Ws21分别为［14］：

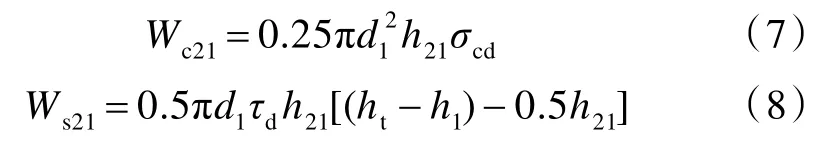
式中，σcd和τd分别为层合板的动压缩反力和动剪切反力；ht为层合板的总厚度；h21为初始压缩波传播子阶段的侵彻深度。

在初始压缩波传播子阶段，弹体的运动方程为

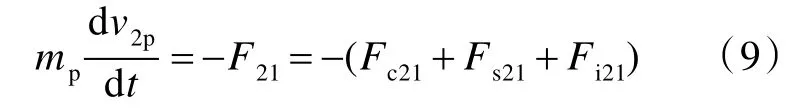
式中，v2p，F21，Fc21，Fs21和Fi21分别为初始压缩传播子阶段弹体的瞬时速度、层合板的总抗力、压缩反力、剪切反力和侵彻区惯性反力。各反力的表达式可参见文献［14］。

令v2p=v2p(t)，则在初始压缩波传播子阶段，弹体的侵彻深度h21为

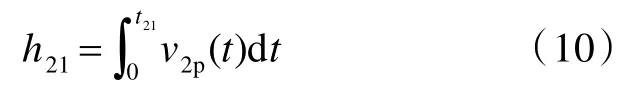
在反射拉伸波传播子阶段，层合板的压缩耗能Wc22和剪切耗能Ws22分别为［14］：

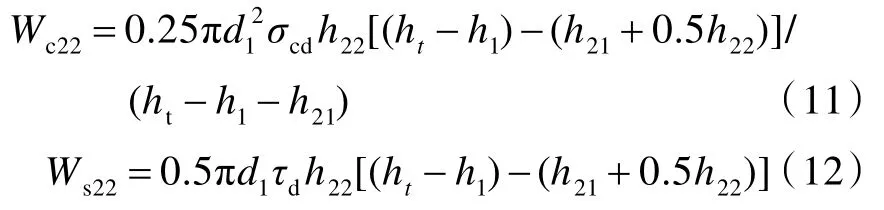
在反射拉伸波传播子阶段，弹体的运动方程为

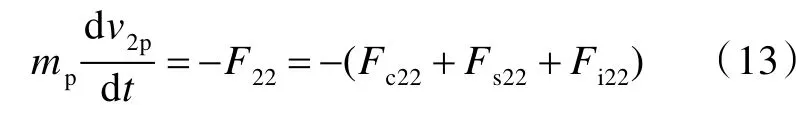
式中，F22，Fc22，Fs22和Fi22分别为反射拉伸波传播子阶段层合板的总抗力、压缩反力、剪切反力和侵彻区惯性反力。各反力的表达式可参见文献［14］。

在反射拉伸波传播子阶段，弹体的侵彻深度h22为

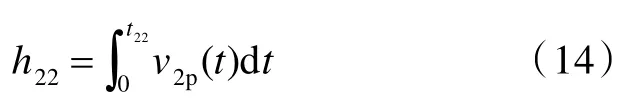
因此，剪切压缩阶段弹体的总侵彻深度h2为

剪切压缩阶段弹体损失的总动能，即层合板吸收的总能量W2为

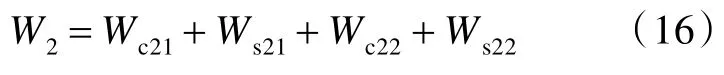
2.3 拉伸变形阶段

拉伸变形阶段也分2 个子阶段，即变形锥的形成及扩展子阶段与变形锥纤维层逐步失效子阶段。变形锥的形成及扩展子阶段从变形的形成开始，至变形锥达到极限变形状态，该状态下的变形锥角满足条件

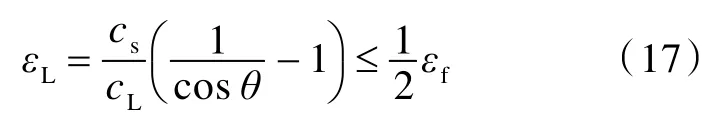
式中：εL和εf分别为纤维层的平均应变和拉伸失效应变；cs和cL分别为层合板的剪切应力波速和拉伸应力波速。由此，可得变形锥的极限变形锥角θε为

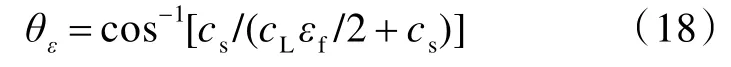
变形锥形成及扩展子阶段的吸能主要包括过渡区分层吸能Ede31和变形锥弹性变形能EED，分别为［14］：

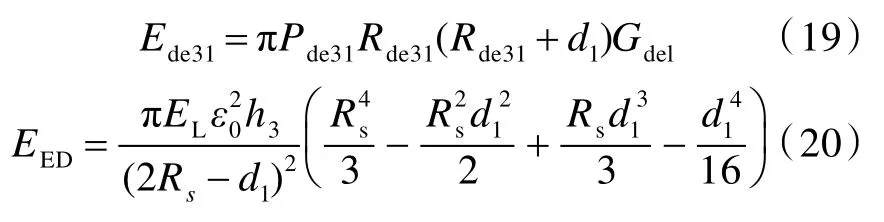
式中：Pde31为分层折减系数；Gdel为层合板层间断裂韧性值；Rde31为裂纹传播半径，Rde31=cdelt31，其中cdel为层间裂纹传播速度；Rs取为变形锥扩展至极限状态时的锥半径值；EL为层合板的拉伸模量；ε0为侵倾区边缘，即r=d1/2 处纤维层的应变，当变形锥达到极限状态时，有ε0=εf；h3为层合板背层未穿透纤维层的厚度，h3=ht-h1-h2。在变形锥纤维层逐步失效子阶段，由于弹体的动能不足以使变形锥所有的纤维层全部失效，即不能穿透层合板，因而出现了部分侵彻的情形（图1（d））。令该子阶段失效纤维层的厚度为h3p，则变形锥侵彻区纤维层的拉伸断裂吸能ETF为［14］

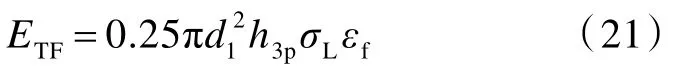
式中，σL为层合板纤维层拉伸强度。此外，变形锥失效纤维层在弹体侵彻过程中还存在分层吸能［14］：

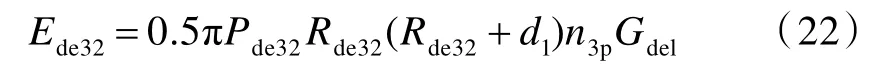
式中：Pde32为分层折减系数；Rde32为裂纹传播半径，Rde32=cdelt32；n3p为变形锥失效纤维层层数，n3p=N·h3p/ht，其中N 为层合板总层数。

由此可得拉伸变形阶段弹体损失的总动能，即层合板吸收的总能量W3为

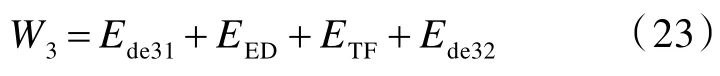
在拉伸变形阶段，弹体的侵彻深度即为变形锥失效纤维层的厚度h3p。

3 弹体侵彻深度计算

在拉伸变形阶段的第1 个子阶段，即变形锥的形成及扩展子阶段，在变形锥未达到极限变形锥角之前，随着弹体的运动，变形锥锥顶会向前运动一定的距离，但在此子阶段，变形锥纤维层并未失效，弹体并未穿透纤维层。因此，为与弹体侵彻深度的一般定义相一致，本文弹体的侵彻深度定义为由弹体侵彻所引起的失效纤维层（包括基体）的总厚度。主要计算过程如下：

1）计算得到开坑墩粗阶段的侵彻深度h1。

2）在剪切压缩阶段，先对初始压缩波传播子阶段进行计算，得到该子阶段的侵彻深度h21。在初始压缩波传播子阶段，若弹体的速度等于0，则弹体总的侵彻深度Dp=h1+h21；初始压缩波传播子阶段结束后，若弹体的速度大于0，则进入反射拉伸波传播子阶段。在反射拉伸波传播子阶段，若弹体的速度等于0，则弹体总侵彻深度Dp=h1+h21+h22。

3）经历了剪切压缩阶段后，若弹体的速度仍大于0，则进入拉伸变形阶段。进入拉伸变形阶段后，若弹体的速度足够大，以致于能够使变形锥达到极限应变状态，即θv≥θε，则弹体完全穿透层合板，此时弹体的侵彻深度Dp=ht。进入拉伸变形阶段后，若弹体的速度不足以使变形锥达到极限应变状态，即θv＜θε，此时变形锥锥角θ 保持不变，且等于θv，其中θv为

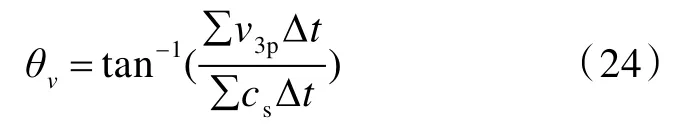
考虑到弹体速度与变形锥角之间存在着相互协调性，则在拉伸变形阶段开始的任意时刻都满足上式，因而有

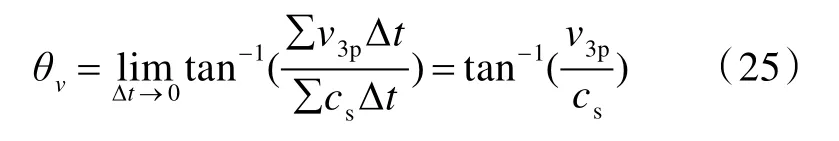
提出上式的理由在于，在变形锥锥角保持为θ=θv的同时，弹体仍具有一定的侵彻能力［13］，从而引起背层未穿透拉伸纤维层的部分失效，即由弹体导致的背层剩余纤维层的部分侵彻。

对拉伸变形阶段侵彻深度h3p的计算，则需根据整个侵彻过程的能量守恒方程得到，该方程为

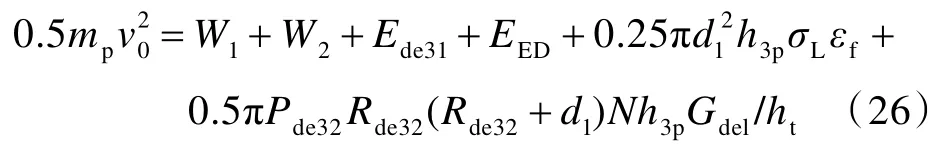
整理后，得到拉伸变形阶段弹体部分侵彻的深度h3p为

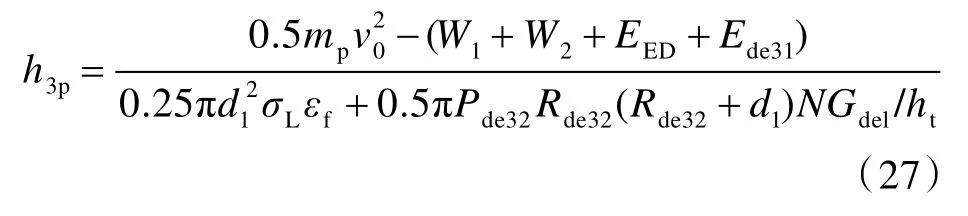
由此，得到部分侵彻情形下弹体的总侵彻深度Dp为

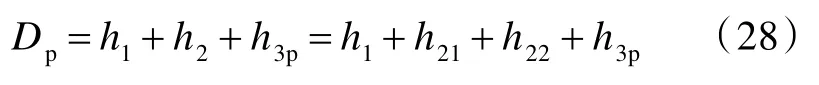
部分侵彻情形下，弹体总侵彻深度的具体计算流程如图3 所示。

4 层合板弹道极限计算

在对弹体侵彻深度进行计算的基础上，通过对弹体侵彻深度及弹体速度的判别，可计算层合厚板的弹道极限速度。计算的主要过程如下：

1）设定一个弹体初始冲击速度值，该速度值小于层合板的弹道极限值。

2）采用上节中的方法计算弹体的侵彻深度，当侵彻深度小于层合板总厚度但弹体速度等于0时，进一步增大弹体初始冲击速度值并重新计算。

3）继续增大弹体初始冲击速度，当弹体的侵彻深度等于层合板总厚度且弹体速度等于0 时，此时弹体的初始冲击速度即为层合板的弹道极限速度值。

图4给出了层合厚板弹道极限的计算流程图。

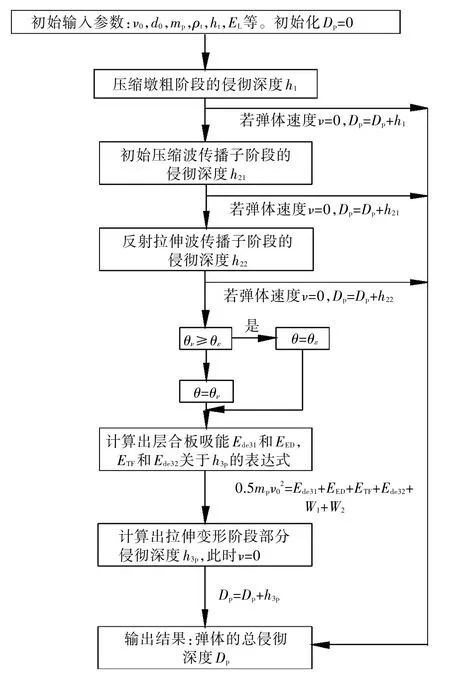
图3 弹体的侵彻深度（DOP）计算流程图Fig.3 Flow chart of DOP calculation of projectiles

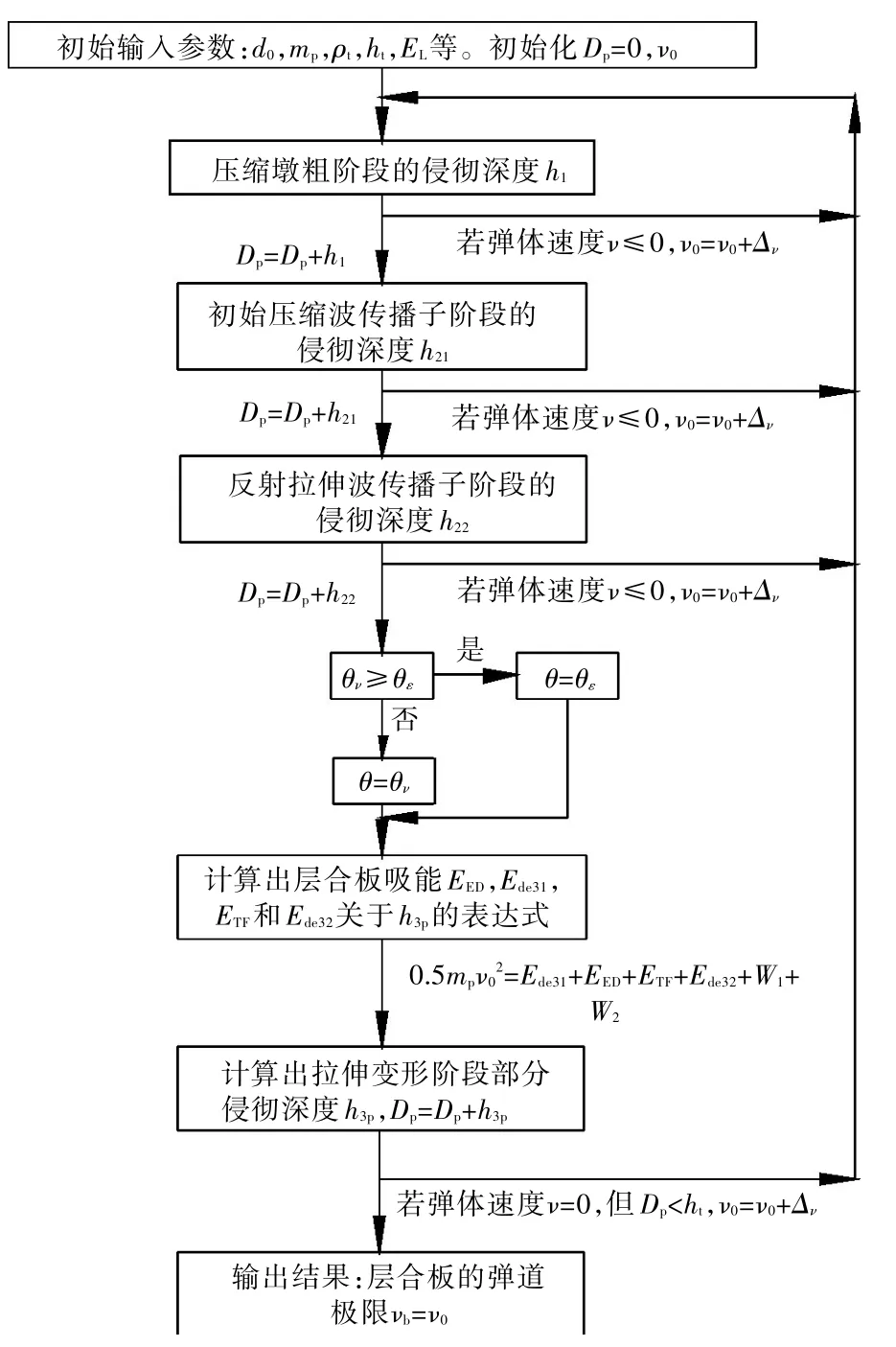
图4 层合厚板弹道极限计算流程图Fig.4 Flow chart of the calculation of ballistic limits for thick laminates

5 试验验证及讨论

5.1 弹体的侵彻深度比较

为了验证本文计算模型的实用性和有效性，首先，将未穿透，即部分侵彻情形下弹体的侵彻深度计算值与文献［5］中的UFRP 层合厚板抗高速侵彻试验结果进行比较，如表1 所示。表中ht，ρA和v0分别为UFRP 层合板总厚度、面密度和弹体初速。计算过程中UFRP 层合板的材料参数参见文献［14］。

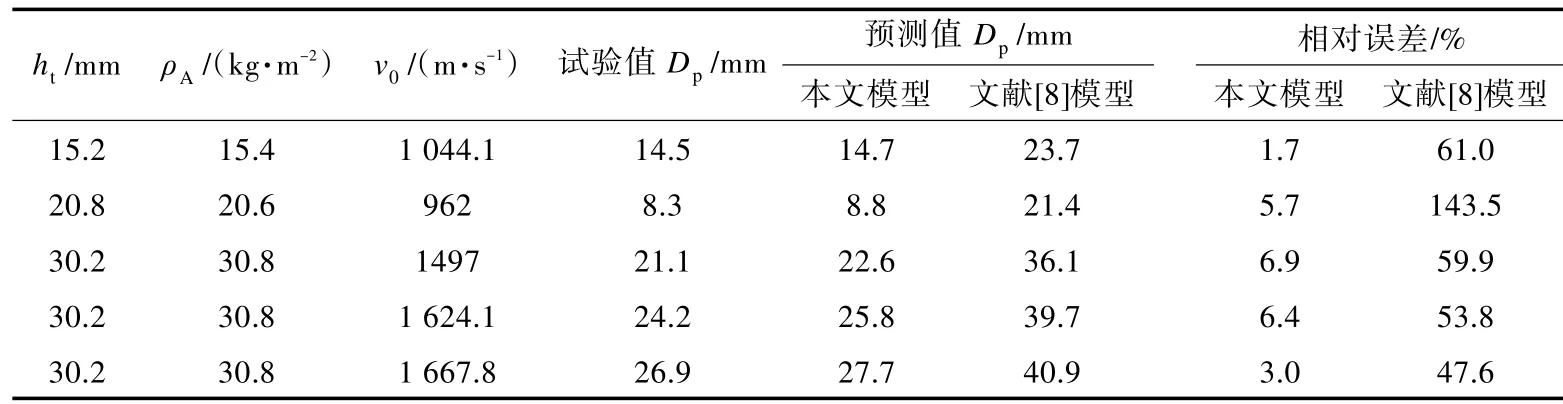
表1 UFRP 层合厚板的侵彻深度（DOP）理论计算值与试验结果［5］的比较Tab.1 Comparison of DOP between theoretically calculated and experimental［5］results for thick UFRP laminates

由表1 可以看出，采用本文理论模型计算得到的弹体侵彻深度与试验结果吻合较好。另从表中还可看出，采用本文理论模型计算得到的弹体侵彻深度较试验值要稍大，这可能与试验中层合厚板材料性质等的差异，尤其是层间剪切强度的影响有关。另外，在弹体侵彻后期，即进入拉伸变形阶段后期，层合板背面未穿透纤维层处于拉剪混合的复杂应力状态，弹体在侵彻未失效纤维层时，除了会受到纤维层产生的拉伸阻力外，还有可能受到剪切阻力。而本文的理论模型中近似认为只有拉伸阻力作用于弹体，从而导致理论计算模型中弹体的侵彻阻力偏小，进而使得理论计算得到的弹体侵彻深度较试验结果稍偏大。此外，理论计算中极限变形锥角的取值也可能与实际试验工况中的极限锥角存在一定的差异，从而影响理论计算的精度。

同时，表1 还给出了采用文献［8］中理论模型计算得到的UFRP 层合厚板侵彻深度值与试验结果的比较。由表可知，采用文献［8］中理论模型计算得到的弹体侵彻深度值和试验值相比要大得多。这主要是由于文献［8］的理论模型是建立在局部化破坏模式假定的基础上，主要针对的是脆性或层间强度较大的层合厚板，其与UFRP 层合厚板抗高速侵彻的破坏机理存在较大差异。尤其是在UFRP 层合厚板拉伸变形阶段，对侵彻深度的影响较大，而文献［8］的理论模型未能很好地考虑到这一点。

5.2 层合板弹道极限比较

进一步采用本文理论模型对层合厚板的弹道极限进行计算，并与文献［5］中的试验结果进行比较，如表2 所示。由表2 可知，采用本文理论模型计算得到的层合厚板的弹道极限值与试验结果吻合较好。另从表2 中还可看出，由本文理论模型计算得到的层合厚板弹道极限值和试验值相比稍小。这主要是由于在采用本文理论模型计算弹道极限的过程中，是逐步增大弹体速度来使弹体刚好达到临界穿透（图1（e）），而此时变形锥处于拉剪混合的复杂应力状态，变形锥没有达到极限变形锥角θε即开始出现纤维层失效，致使弹体更容易穿透变形锥后续的纤维层，因而使得弹体穿透变形锥所需的动能偏小，从而导致层合厚板的弹道极限值偏低。

另外，表2 还给出了采用文献［8］的理论模型计算得到的UFRP 层合厚板的弹道极限值，并与文献［5］的试验结果进行了比较。从表中可看出，采用文献［8］的理论模型计算得到的UFRP 层合厚板弹道极限值较试验结果低得多。这主要是由2 方面的原因所致：一方面，文献［8］中的模型并没有考虑UFRP 层合厚板抗高速侵彻过程中弹体镦粗变形的影响，使得该模型在整个侵彻过程的计算中层合板的阻抗力被低估，从而导致计算得到的层合板的总吸能偏低；另一方面，文献［8］中模型不能很好地考虑UFRP 层合厚板拉伸变形效应的影响，致使对UFRP 层合厚板背面纤维层，即拉伸变形阶段变形锥纤维层变形和失效的吸能计算偏低。因此，采用文献［8］中模型计算得到的UFRP 层合厚板的总吸能严重偏低，从而导致采用该模型计算得到的UFRP 层合厚板的弹道极限值要远低于试验值。

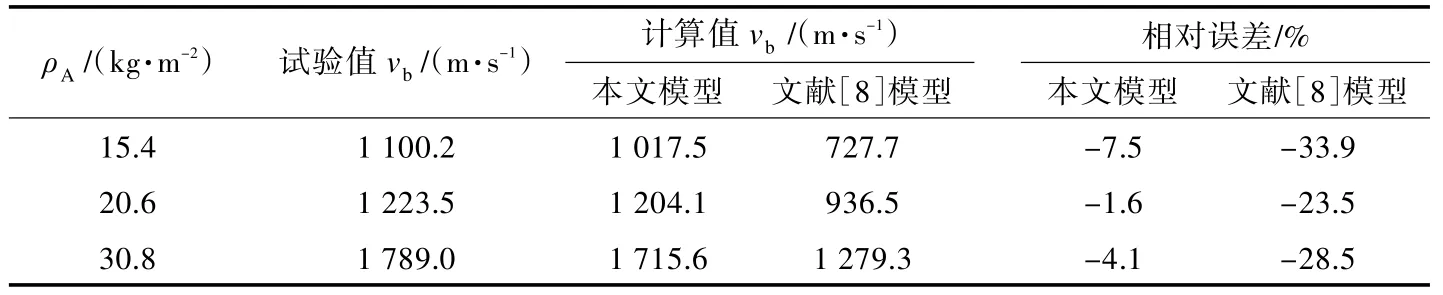
表2 理论计算UFRP 层合厚板弹道极限值与试验结果［5］的比较Tab.2 Comparison of theoretical and experimental［5］results of ballistic limits for thick UFRP laminates

从上面的对比分析可得出，本文给出的理论计算模型能对UFRP 层合厚板抗高速钝头弹侵彻的弹体侵彻深度和层合板弹道极限进行合理且较为准确的预测。不过，应该指出的是，由于弹速及靶板厚度不同，可能会导致侵彻机理出现差异，因而本文模型对速度较低的情形（＜800 m/s）或靶板较薄的情形（ht/d ＜2）误差可能会较大。

6 结 语

通过对UFRP 层合厚板抗高速侵彻过程的分析，将整个抗侵彻过程分为了开坑镦粗、剪切压缩和拉伸变形3 个阶段，并基于能量守恒原理建立了UFRP 层合厚板抗高速钝头弹侵彻的三阶段理论计算模型。利用该模型，对部分侵彻情形下弹体的侵彻深度以及UFRP 层合厚板的弹道极限速度进行了计算，理论计算得到的弹体侵彻深度和层合厚板的弹道极限值均与相应的试验结果吻合较好，验证了理论模型的实用性和有效性。而通过与试验结果的比较表明，本文建立的理论模型能对UFRP 层合厚板抗高速钝头弹侵彻的弹体侵彻深度和层合厚板弹道极限进行合理的预测，可以降低试验成本，具有一定的理论和工程应用价值。

［1］JACOBS M J N，VAN DINGENEN J L J. Ballistic pro⁃tection mechanisms in personal armour［J］. Journal of Materials Science，2001，36（13）：3137-3142.

［2］梁子青，周庆，邱冠雄，等.超高分子量聚乙烯纤维防弹复合材料的研究［J］. 天津工业大学学报，2003，22（2）：6-9.LIANG Ziqing，ZHOU Qing，QIU Guanxiong，et al.Study on ultra-high molecular weight polyethylene anti⁃ballistic composites［J］. Journal of Tianjin Polytechnic University，2003，22（2）：6-9.

［3］TAN V B C，KHOO K J L. Perforation of flexible lami⁃nates by projectiles of different geometry［J］. Interna⁃tional Journal of Impact Engineering，2005，31（7）：793-810.

［4］顾冰芳，龚烈航，徐国跃.UHMWPE 纤维复合材料防弹机理和性能［J］.纤维复合材料，2006（1）：20-23.GU Bingfang，GONG Liehang，XU Guoyue.Ballistic re⁃sistance mechanism and performance of UHMWPE composites［J］.Fiber Composites，2006（1）：20-23.

［5］王晓强，朱锡，梅志远，等.超高分子量聚乙烯纤维增强层合厚板抗弹性能实验研究［J］. 爆炸与冲击，2009，29（1）：29-34.WANG Xiaoqiang，ZHU Xi，MEI Zhiyuan，et al. Ballis⁃tic performances of ultra-high molecular weight poly⁃ethylene fiber-reinforced thick laminated plates［J］.Explosion and Shock Waves，2009，29（1）：29-34.

［6］王晓强，朱锡，梅志远.高速钢质破片侵彻高强聚乙烯纤维增强塑料层合板试验研究［J］. 兵工学报，2009，30（12）：1574-1578.WANG Xiaoqiang，ZHU Xi，MEI Zhiyuan. An experi⁃mental research on high velocity steel fragments perfo⁃rating UHMWPE FRP laminates［J］. Acta Armamenta⁃rii，2009，30（12）：1574-1578.

［7］WEN H M. Predicting the penetration and perforation of FRP laminates struck normally by projectiles with different nose shapes［J］. Composite Structures，2000，49（3）：321-329.

［8］WEN H M. Penetration and perforation of thick FRP laminates［J］. Composites Science and Technology，2001，61（8）：1163-1172.

［9］覃悦，文鹤鸣，何涛.卵形弹丸撞击下FRP 层合板的侵彻和穿透［J］. 复合材料学报，2007，24（2）：131-136.QIN Yue，WEN Heming，HE Tao. Penetration and per⁃foration of FRP laminates under normal impact［J］. Ac⁃ta Materiae Compositae Sinica，2007，24（2）：131-136.

［10］NAIK N K，SHRIRAO P. Composite structures under ballistic impact［J］. Composite Structures，2004，66（1/4）：579-590.

［11］NAIK N K，SHRIRAO P，REDDY B C K. Ballistic impact behaviour of woven fabric composites：formula⁃tion［J］. International Journal of Impact Engineering，2006，32（9）：1521-1552.

［12］古兴瑾，许希武，黄晶.层合复合材料薄板高速冲击损伤研究［J］. 南京航空航天大学学报，2008，40（3）：370-375.GU Xingjin，XU Xiwu，HUANG Jing. High velocity impact damage of thin composite laminates［J］. Jour⁃nal of Nanjing University of Aeronautics and Astro⁃nautics，2008，40（3）：370-375.

［13］梅志远，朱锡，张立军.FRC 层合板抗高速冲击机理研究［J］.复合材料学报，2006，23（2）：143-149.MEI Zhiyuan，ZHU Xi，ZHANG Lijun. Ballistic pro⁃tective mechanism of FRC laminates［J］. Acta Materi⁃ae Compositae Sinica，2006，23（2）：143-149.

［14］陈长海，朱锡，王俊森，等. 高速钝头弹侵彻中厚高强聚乙烯纤维增强塑料层合板的机制［J］. 复合材料学报，2013，30（5）：226-235.CHEN Changhai，ZHU Xi，WANG Junsen，et al.Mechanism of high-velocity blunt-nosed projectiles penetrating moderately thick UHMWPE fiber rein⁃forced plastic laminate［J］. Acta Materiae Compositae Sinica，2013，30（5）：226-235.

［15］张晓晴，杨桂通，黄小清.柱形平头弹体墩粗变形的理论分析［J］. 华南理工大学学报（自然科学版），2005，33（1）：32-36.ZHANG Xiaoqing，YANG Guitong，HUANG Xiaoq⁃ing. Theoretical analysis of the mushrooming deforma⁃tion of flattened cylindrical projectile［J］. Journal of South China University of Technology（Natural Sci⁃ence Edition），2005，33（1）：32-36.