不规则曲线拟合质量评定方法的改进

范玉茹，师 岩，张幼群，徐 栋

（1.61206 部队， 北京 100042）

不规则曲线拟合质量评定方法的改进

范玉茹1，师 岩1，张幼群1，徐 栋1

（1.61206 部队， 北京 100042）

不规则曲线拟合时，需要按最优原则依据曲线的形状来选择拟合函数，构造函数模型。给定数据点的多少以及数据的拟合方向对曲线拟合也会产生影响，因此需要对曲线进行最佳的拟合。衡量曲线拟合模型误差的精度时，要求观测数据的方差相同且观测数据的协方差为零，这与一般的实际情况不符。因此，在曲线最佳拟合的基础上，对评定曲线拟合精度的质量标准方法进行了改进，从不规则曲线拟合的精度及形状2个方面进行了评价。

不规则曲线；质量评定；协方差；最佳拟合

矢量地图数据采集无论直接方法还是间接方法，都面临曲线的处理。常见的有等高线、水系、曲线道路等不规则形状的表示。由于直接方法或间接方法所采集的数据都只能是曲线的有限点，因此，对曲线的处理有插值和拟合2种方法，前者是将采集数据当作无误差处理，后者则是将采集的数据看作含有误差。对于测量工作而言，只要是数据测量，就一定存在误差，因此，对曲线数据的处理常采用拟合的方法。在曲线拟合时，选择函数模型比较关键。选用拟合函数不同，会产生不同的拟合效果，因此需要按最优原则依据曲线的形状来选择拟合函数，构造函数模型。除此之外，给定数据点的多少对曲线拟合也会产生影响。曲线拟合的误差分为曲线模型误差和曲线拟合的偶然误差2个部分。对曲线进行最佳拟合的原则是综合考虑系统误差和偶然误差的联合影响，将模型误差和数据误差对曲线拟合的影响减小到最小。对矢量地图数据拟合曲线的精度评定，不仅要考虑已知数据的偶然误差，而且要考虑拟合曲线的模型误差，应该将两者结合起来完整地去评价拟合曲线的质量。在文献[1]中，蓝悦明采用最小二乘拟合曲线，综合考虑曲线拟合的两种误差影响，采用均方误差MSE（δ）来衡量曲线拟合模型的精度，对各拟合方程的均方误差进行比较，MSE（δ）最小的即为最佳曲线拟合方程。

式中，X、Y为拟合曲线的纵横坐标；β为拟合曲线参数；ε为拟合的模型误差；Δ为拟合数据Y的偶然误差，且E（Δ）=0；n为拟合曲线的观测个数；t为拟合曲线的参数个数；σ2为观测数据方差；I为单位矩阵。

但是，使用MSE（δ）来衡量曲线拟合模型误差的精度时，要求观测数据的方差相同且观测数据的协方差为零，这与一般的实际情况不符。因此，需要对评定曲线拟合精度的质量标准进行探讨。

1 不规则曲线的最佳拟合

由于最小二乘估计具有无偏性、一致性和有效性，目前曲线拟合的方法多采用最小二乘拟合法，拟合方向一般选用X方向，将Y方向作为真值，使残差的平方和最小，即

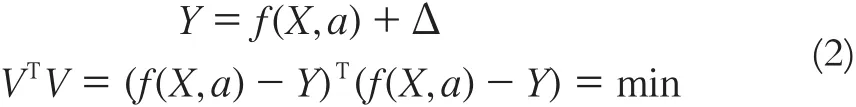
式中，X、Y为观测点的值；a为曲线待定参数。

实际上，无论是x坐标还是y坐标都为观测值，均含有偶然误差，当采集的数据在拟合方向发生剧烈变化时如图1第4、5、6点，在选用的某一定方向拟合是值得探讨的[2,3]。

图 1 2种方式的曲线拟合

最佳地拟合各观测点的估计曲线，应使各观测点到估计曲线的正交距离残差平方和最小，如图1b所示，用式子表示即

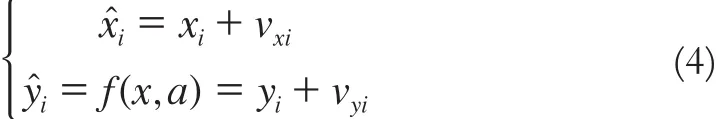
取坐标xi和待求参数a为未知数，令

则：

方程中的观测个数为2m，未知数个数为m+n+1，其矩阵表达式为：

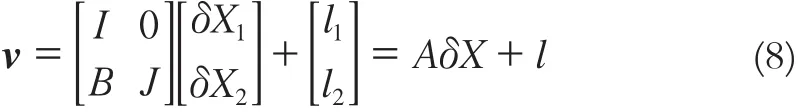
式（8）中，I为单位矩阵，B为m阶对角矩阵，表示为：

按式（4），采用参数平差得：

单位权中误差为：

2 曲线拟合评定的改进

由已知点数据来拟合曲线其形状位置是不确定的，如图2所示。给定点本身的位置误差可以根据点的方差-协方差来定量地描述，但是，对于曲线模型的不确定性，通常难以定量化描述，因为根据已知点能构成的曲线很多，只能在一定的范围内给其不确定性[4,5]。

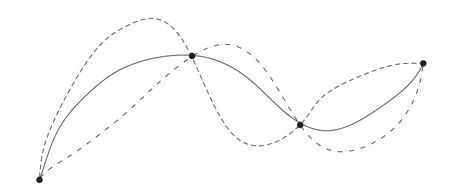
图 2 数据拟合的不确定性

在曲线拟合时，对于给定的2点间最大偏差h，可以由给定的2点间长度S和拟合曲线方程来确定，如图3所示。当选择不同的拟合函数模型时，将会得到不同的值。

图 3 曲线拟合2点间长度s和最大偏差h

对于曲线拟合的原始离散点，它们均含有一定的测量误差，如图4所示。实线为真实曲线，虚线为拟合曲线，显然h1为离散点拟合曲线的最大误差。对于原始曲线，h1是固定的，可以采用不同的拟合模型来拟合曲线，拟合后的h^1与原始曲线的h1存在偏差通过多次拟合试验可得，Δ h1可反映出点M1的拟合误差，依次可以采用整条曲线的来衡量拟合曲线的精度。

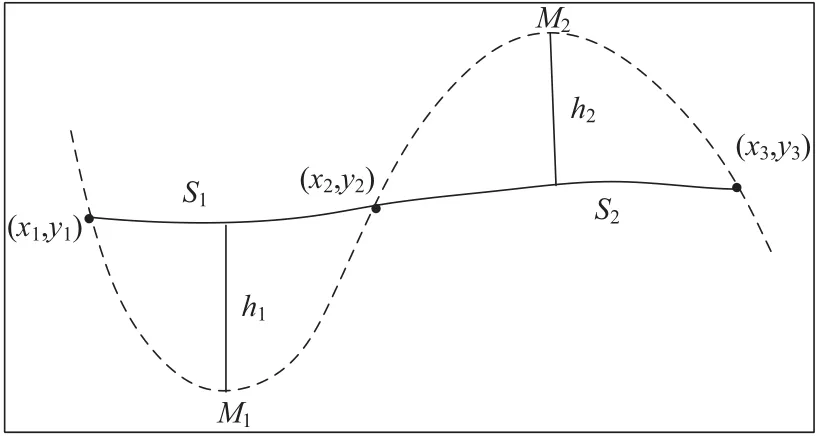
图 4 曲线拟合误差

由于拟合曲线时，是采用曲线上的特征点来拟合的，特征点在一定程度上代表了曲线的形状，也是曲线精简的过程。特征点的提取可参见文献[6]，在上一级特征点提取后，两相邻特征点之间的曲线段上距这2个相邻特征点间直线偏差最大的点，如图5所示，由此可通过计算特征点的h值来替代真实曲线上的h值。图5中点（xi，yi）到点（xi-1，yi-1）和点（xi+1，yi+1）所连直线的垂直距离为[6]：

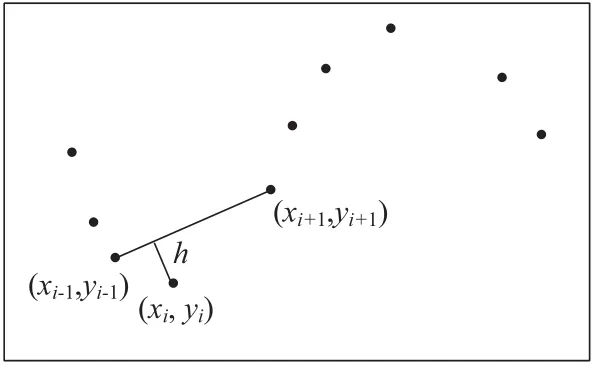
图 5 除端点外的离散数据h值

3 实例分析

采用文献[1]的拟合数据，同一幅图上取一组数字化点，其数字化精度为σ=0．3 mm，数据见表1。分别按式（12）～（14）拟合，拟合结果如图6所示，拟合精度见表2。

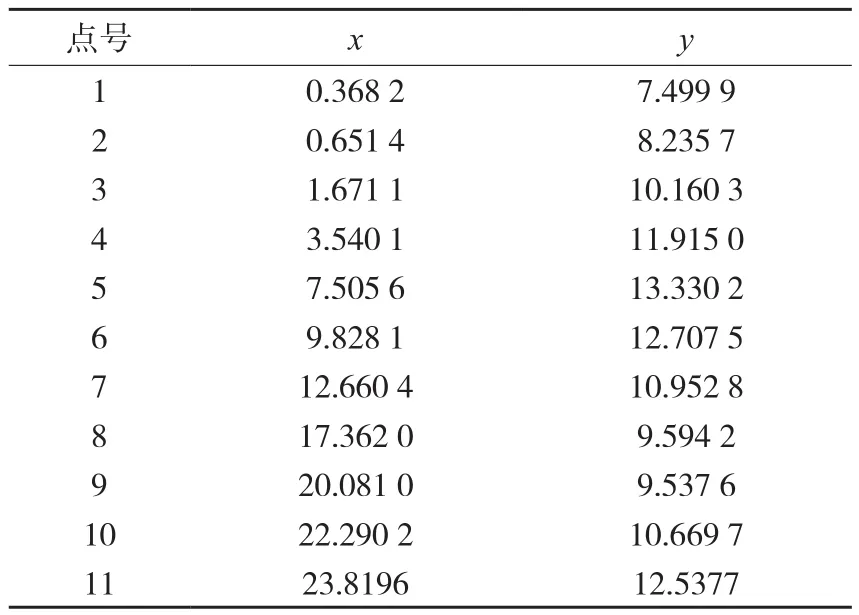
表 1 数字化的X、Y坐标值/mm

表 2 数据拟合比较

由表2可以看出，对于第二组数据不管采用哪种方法，四次多项式拟合的效果比较好。采用正交最小二乘，在拟合精度和拟合效果上都优于在y方向的最小二乘拟合。

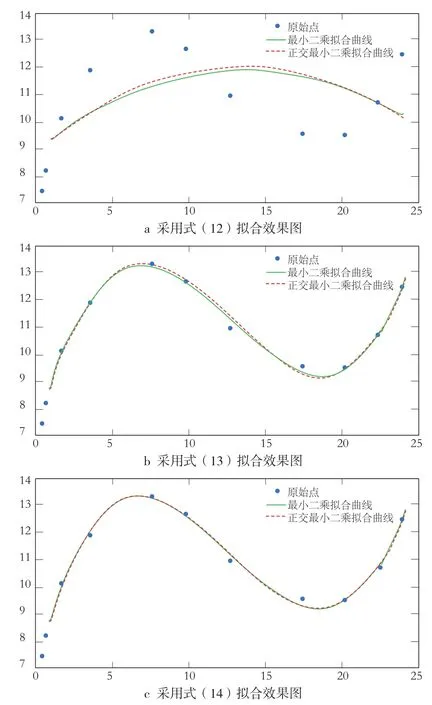
图 6 数据拟合效果图

4 结 语

1）自变量误差较小时，可以忽略自变量误差，对拟合参数的影响较小，采用普通最小二乘法计算简单实用。如果自变量误差较大，忽略自变量的误差就会影响参数的大小，此时应该顾及自变量的误差。

2）正交距离曲线拟合，同时顾及了因变量和自变量的误差，以正交距离的残差平方和最小为原则，拟合结果从整体意义上保持最佳，从几何意义上，其曲线拟合更合理，改进了普通最小二乘使拟合曲线沿一个方向与实际曲线逼近的效果。

（ ）参考文献

[1] 蓝悦明．空间位置数据不确定性问题的若干理论研究[D]．武汉: 武汉大学, 2003

[2] CLesort N C．Statistical Efficiency of Curve Fitting Algorithoms [J]．Computational Statistics＆Data Analysis,2004 (47):713-728

[3] 丁克良，鸥吉坤，赵春梅．正交最小二乘曲线拟合法[J]．测绘科学,2007(5):18-20

[4] 许谷声．地理信息系统(GIS)中不规则曲线的不确定性和精度分析[D]．上海:同济大学，1999

[5] 许谷声，童小华．一种GIS中不规则曲线数字化的精度评定方法[J]．同济大学学报，2002(11) :1 361-1 364

[6] Reynders E，Pintelon R，Roeck G．Uncertainty Bounds on Modal Parameters Obtained from Stochastic Subspace Identification[J]．Mechanical Systems and Signal Processing, 2008(22):948-969

[7] Liu W，Yang W．Estimating Coordinates of a 2D—Point from Multiple Observations[J]．Computers＆Geosciences, 2006(32): 1 235-1 246

[8] Ewen J，Donnell G，Burton A，et al．Errors and Uncertainty in Physically—Based Rainfall一 Runoff Modelling of Catchment Change Effects[J]．Journal of Hydrology ,2006(330):641-650

[9] Liu Y，Wu L，Mao T．A Direct Error Measure Method for Linear Features Occurred in Digitalization Processes in GIS,2003

P208

B

1672-4623（2015）02-0134-03

10.3969/j.issn.1672-4623.2015.02.047

范玉茹，博士，工程师，主要研究方向为GIS数据质量控制与评价。

2014-04-17。

项目来源：国家自然科学基金资助项目（41274016）。