GPS多频观测数据的模拟仿真

张宏强，刘 源，陈俊平，席志龙

（1.内蒙古自治区测绘地理信息局，内蒙古 呼和浩特 010010；2.中国地质大学 信息工程学院，湖北 武汉 430074）

GPS多频观测数据的模拟仿真

张宏强1，刘 源2，陈俊平2，席志龙2

（1.内蒙古自治区测绘地理信息局，内蒙古 呼和浩特 010010；2.中国地质大学 信息工程学院，湖北 武汉 430074）

GPS现代化后增加了L5频率，多个频率观测值的使用可以组成更多的线性组合。但由于目前很难获取L5的实测载波数据，只能在双频载波的基础上通过多频载波相位观测值和伪距观测值的模拟模型获取L5载波的模拟数据。探讨了利用非差思想对L5进行数值模拟的方法，以相同方法模拟不同采样率下的L2载波数据并与实测的L2载波数据进行对比分析，验证了该模拟方法在高采样率下的可行性。

L5频率；非差观测值；载波相位；伪距

为了研究多频观测组合在消除电离层、对流层等观测误差影响后对周跳探测能力的影响，需要对GPS多频观测数据进行模拟仿真。目前，模拟L5观测数据的方法主要有2种[1]：L5非差观测值模拟方法和L5双差观测值模拟方法。本文主要是以第1种方法进行模拟，采用VB语言编写程序，分别对1 s、5 s、10 s采样率下的L2载波数据与实测的L2载波数据进行对比分析，验证了L5非差观测值模拟方法的可行性。

1 载波相位观测值的模拟

在历元t1时刻，L1、L2、L53个频率的载波相位观测值分别为φ1（t1）、φ2（t1）、φ5（t1），在历元t2时刻，L1、L2、L53个频率的载波相位观测值分别为φ1（t2）、φ2（t2）、φ5（t2）。在t1时刻，L1频率的观测方程为[2]：

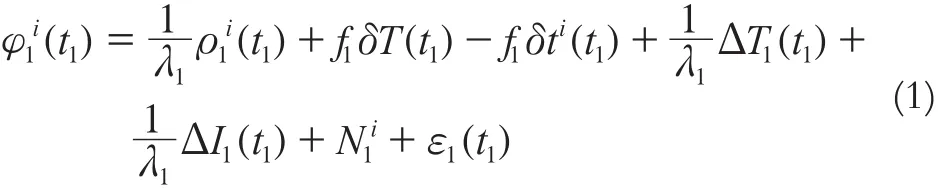
在t2时刻，L1频率的观测方程为[2]：

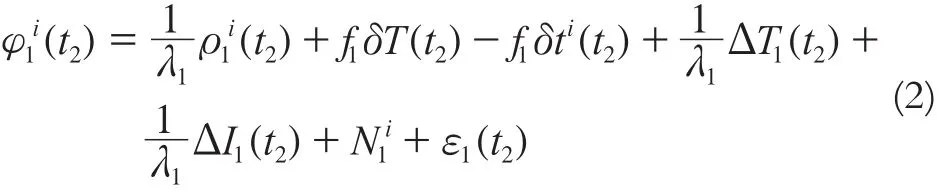
由式（1）减去式（2）可以得出历元t1、t2之间的单差：

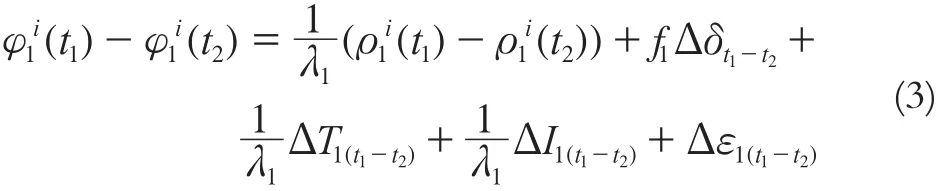
同理可以得出L2、L5在历元t1、t2之间的单差：

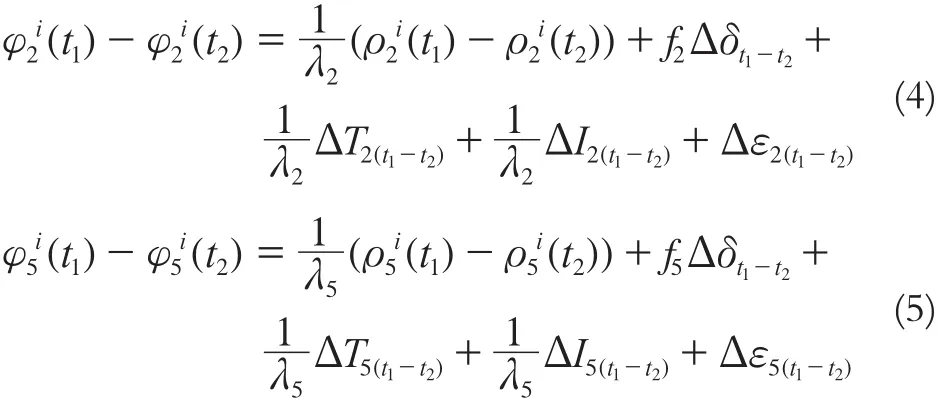
式中，Δ T1（t1-t2）、Δ T2（t1-t2）、Δ T5（t1-t2）分别为L1、L2、L5频率在t1、t2时刻的对流层延迟误差之差；Δ I1（t1-t2）、Δ I2（t1-t2）、Δ I5（t1-t2）分别为L1、L2、L5频率在t1、t2时刻的电离层误差之差。由于在同一个历元时刻，同一台接收机对卫星i的几何距离ρ、接收机的钟差以及卫星钟差、对流层延迟误差都是一样的，所以式（3）、式（4）、式（5）相减可以得出：

根据各频率与电离层误差之间的关系[3]：

将式（10）、式（11）分别代入式（8）、式（9），得出：

GPS双频载波与电离层有如下关系[4]：

ΔI( t ) = λ[ φi(t) +Ni- f1(φi(t) +Ni)]f22(14)

11 111 1 f221 2f22-f12

ΔI( t ) = λ[ φi(t) +Ni- f1(φi(t) +Ni)]f22(15)

12 112 1 f222 2 f2-f221

将式（14）、式（15）相减，则：

根据式（12）、式（13）、式（16），可以得出L2、L5在历元之间的模拟载波观测差值[5]：

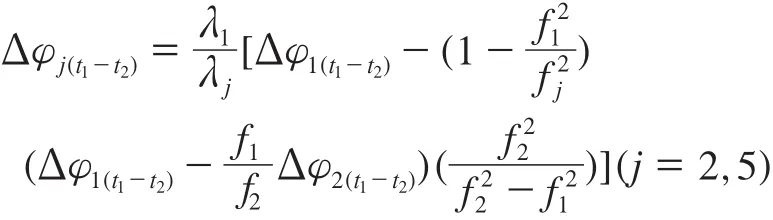
由于GPS的实际观测数据中含有随机噪声，故在模拟的L5数据中也引入随机噪声，由程序直接生成一组（[-0.01,+0.01]周）内的随机数附加在每个历元的数据上。

2 伪距观测值的模拟

在同一历元t时刻，伪距观测方程为[6]：

Pj(t)=ρj(t)+c(δT(t)-δt(t))+Δ Tj(t)+Δ Ij(t)+εj(t) (17)式中，j=1,2,5；Pj（t）为接收机到卫星的伪距观测值；Pj（t）为接收机到卫星的几何距离；δT（t）- δt （t）为t时刻卫星钟差和接收机钟差之间的差值；Δ Tj（t）为t时刻的对流层延迟误差；Δ Ij（t）为t时刻的电离层误差；εj（t）为t时刻的随机观测噪声。

由各频率的伪距观测值相减可以得出：

GPS观测数据的P码和电离层有以下关系[7]：

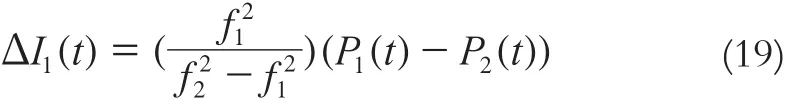
故L5频率各历元的模拟伪距观测值可以表示为：

随机噪声同载波相位观测值一样，也可以由程序直接生成一组（C/A码区间[-3.0 m,+3.0 m]，P码区间为[-0.3 m,+0.3 m]）内的随机数附加在每个历元的数据上。

3 模拟数据程序设计

L5数据模拟模块主要包括L5载波数据的模拟，L5伪距观测值的模拟，L2历元间真实载波差值与模拟值之差的计算以及载波值模拟方法精度残差4部分。在提取某一颗卫星的载波和码伪距数据以后，根据波长和频率的关系，可以通过L1载波、L2载波历元间的差值来模拟L5载波数据在历元间的差值，利用C1码以及P2码可以模拟出L5伪距观测值。为了检验L5载波模拟的精度，可以通过模拟L2载波与真实的L2载波进行比较，并画出载波值模拟方法精度残差图。L5数据模拟算法实现的部分代码如下：

Private Sub mnuL5zaibochazhi_Click() 模拟L5载波数据

Open "选择卫星PRN编号的观测值.txt" For Input As #1读取所选卫星的原始载波数据Open App.Path & "" & w1 & "卫星历元间单差的模拟L5载波数据" & ".txt"

For Output As #2 输出卫星历元间单差的模拟L5载波数据

Print #2, w1 & "卫星历元间单差的模拟L5载波数据"

Private Sub mnuL5weijuzhi_Click() 模拟L5伪距值

Print #2, w1 & "卫星历元间单差的模拟L5伪距值"

Private Sub mnuL2zaibochazhi_Click() 差值与模拟值之差

Print #2, w1 & "卫星历元间L2的载波差值与模拟值之差"

Private Sub mnujingducancha_Click() 差值与模拟值比较图

jingdutu.TChart1.Export.SaveToJPEGFile (w1 & "卫星历元间L2的载波差值与模拟值比较图.jpeg"), False,jpegBestQuality, 200, 780, 620 输出比较图

4 多频观测数据的模拟流程及模拟结果对比分析

根据多频观测数据中各频率之间的关系以及观测误差模型，模拟出L5频率的数据。模拟流程如图1所示。

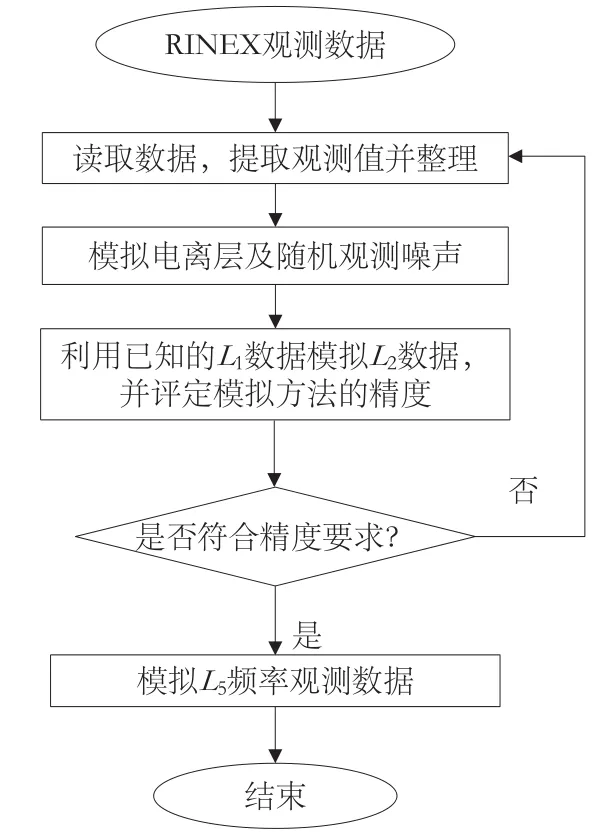
图1 L5频率数据模拟流程图

取某地区的GPS双频观测数据作为模拟多频观测值的原始数据，采样率间隔分别为1 s、5 s、10 s。现选取原始数据中PRN03号卫星的数据来模拟多频观测数据，模拟结果对比表中的数据仅为观测数据的一部分，1 s采样率观测数据模拟结果对比分析见表1、图2。

表1 1 s采样率下多频观测数据模拟结果对比表/周

由图2可以看出，1 s采样率时历元间实测的L2载波差值与模拟值之差在-0.103与-0.075周范围内，差值大部分集中在-0.087周左右，符合模拟的精度要求。此时由于1 s的数据采样率，能够很好地反映并模拟出电离层起伏，因此，解算出的中误差很小，为0.018 065 周，所以1 s采样率下模拟的多频观测数据是比较符合真实观测数据环境的。

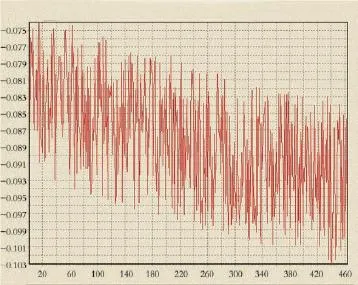
图2 1 s采样率下多频观测数据模拟结果对比图

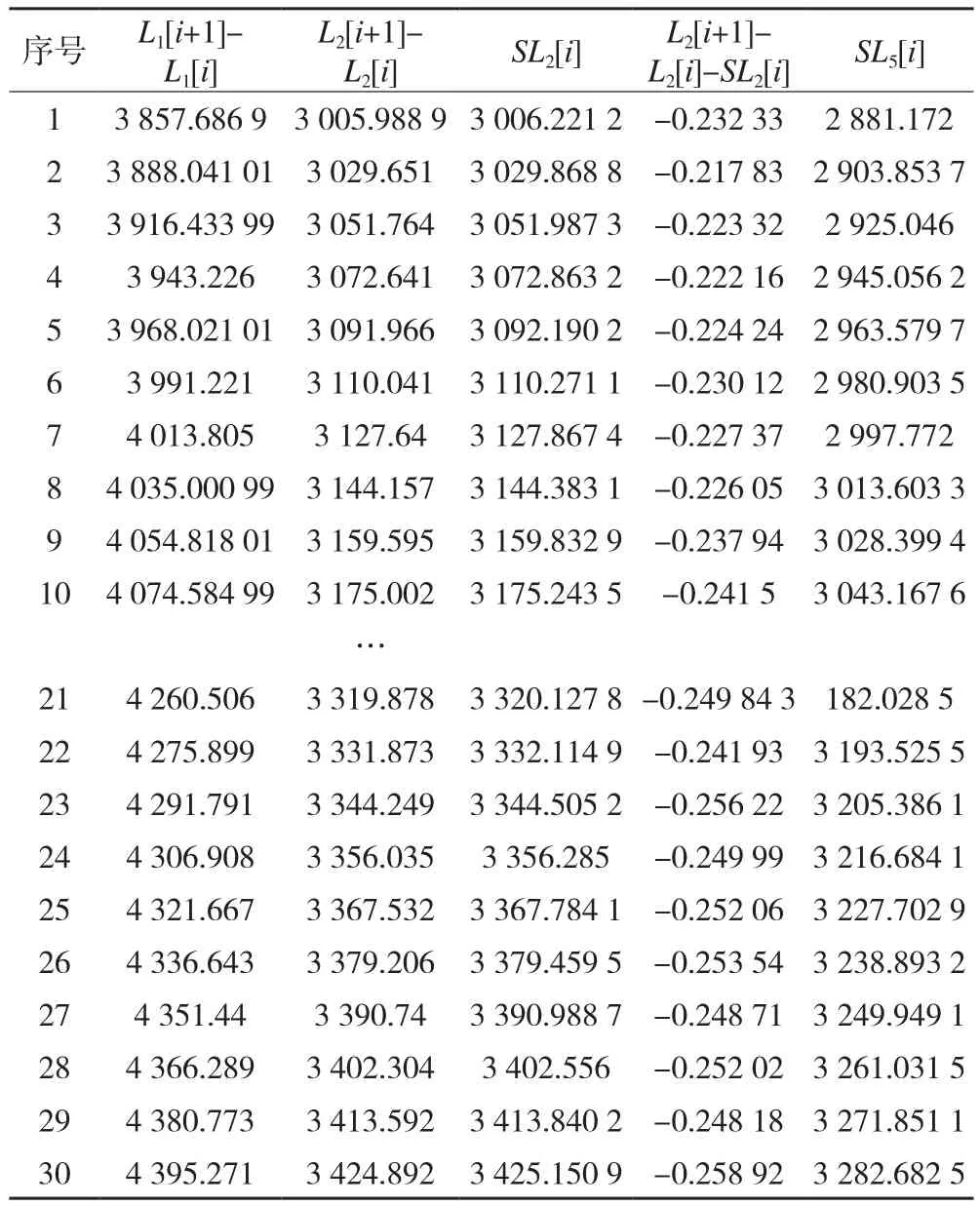
表2 5 s采样率下多频观测数据模拟结果对比表/周

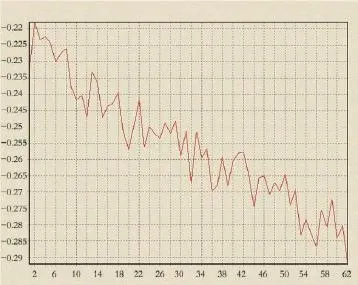
图3 5 s采样率下多频观测数据模拟结果对比图

由表2、图3可以看出，5 s采样率时历元间实测的L2载波差值与模拟值之差在-0.29与-0.22周范围内，与采样率为1 s的模拟数据精度相比较，采样率为5 s数据的模拟精度要低一些，但是仍然符合模拟的精度要求。由于5 s的数据采样率对反映并模拟电离层的起伏有一定的偏差，因此解算出的实测L2载波差值与模拟值之差有所增大，中误差也相对增大，最大值为0.258 92周，中误差为0.241 353。

表3 10 s采样率下多频观测数据模拟结果对比表/周

图4 10 s采样率下多频观测数据模拟结果对比图

由表3、图4可以看出，10 s采样率时历元间真实的L2载波差值与模拟值之差在-1.15与-0.99周范围内，相对前两种采样率来说，10 s的采样率模拟的数据与真实数据相比偏差比较大，达到了1周左右。由于10 s采样率对反映并模拟电离层起伏已经有很大的偏差，因此解算出的实测L2载波差值与模拟值之差较大，中误差也相对增大。

从图2～图4也可以清楚地看出，真实的L2载波与模拟的L2载波差值始终为负值，而且不呈正态分布，表明这种差值不属于偶然误差，是系统误差。引起这些系统误差的原因可能是由于多路径效应或者随机噪声等等。上述图表表明，随着采样率时间的变长，在相同历元间的不同采样率（1 s、5 s、10 s）的L2载波的真实值与模拟值之间的偏差呈增大趋势，但变化范围很小。当采样率为1 s时，L2载波的真实值与模拟之间的偏差较小，小于0.1周；当采样率为5 s时，L2载波的真实值与模拟之间的偏差变为0.25周左右，这种偏差在模拟精度之内；当采样率变为10 s甚至更大时，这种偏差会随之增大。引起这种现象的主要原因是该模型的计算主要取决于电离层的起伏，当采样间隔增大时，该模型模拟的电离层放大了电离层误差。

综上所述，当观测数据采样率较小时，用L5非差观测值模拟方法模拟L5载波观测值是可行的，而且模拟的精度较高。但当采样率的间隔较大时，用该方法模拟L5载波观测值时需要考虑电离层以及随机噪声对模拟数据的影响，可以采用精度更高的方法来模拟，比如L5双差观测值模拟方法。

[1] 冯来平. GPS多频观测数据处理方法及应用研究[D]. 郑州:信息工程大学，2009

[2] 李征航，黄劲松. GPS测量与数据处理[M]. 武汉:武汉大学出版社，2009

[3] 周忠谟，易杰军，周琪. GPS卫星测量原理与应用[M]. 北京:测绘出版社，2002

[4] 唐保华，刘庆元，王虎. GPS三频组合观测值的研究[J]. 矿山测量，2007(3):56-59

[5] Wu Y, Jin S G, Wang Z M. Cycle Slip Detection Using Multi-Frequency GPS Carrier phase Observations: A Simulation Study[J]. Advances in Space Research， 2010,46(2):144-149

[6] 韩绍伟. GPS组合观测值的理论及应用[J]. 测绘学报，1995(5):8-13

[7] 汪平，郝金明，刘伟平，等. 使用多频组合观测值探测与修复周跳[J].测绘通报，2009,12(6):12-15

P228.41

B

1672-4623（2015）03-0126-04

10.3969/j.issn.1672-4623.2015.03.044

张宏强，硕士，研究方向为工程测量。

2014-01-06。