基于信誉机制的分布式扩散最小均方算法

卢光跃陈文晓 黄庆东

（西安邮电大学无线网络安全技术国家工程实验室 西安 710121）

基于信誉机制的分布式扩散最小均方算法

卢光跃*陈文晓 黄庆东

（西安邮电大学无线网络安全技术国家工程实验室 西安 710121）

非安全环境中的无线传感器网络（WSN）可能存在恶意攻击节点，恶意节点将会篡改其观测数据以影响参数估计的准确性。为此，该文提出基于信誉机制的分布式扩散最小均方（R-dLMS）算法和扩散归一化最小均方（R-dNLMS）算法。该算法能够根据各节点对整个网络参数估计的贡献来设置相应的信誉值，从而减小恶意节点对网络攻击的影响。仿真结果表明，与无信誉值的算法相比，该算法的性能得到大幅度提高，且R-dNLMS算法在R-dLMS算法的基础上，算法性能得到进一步提升。

无线传感器网络；恶意攻击；分布式；扩散最小均方；信誉值

1 引言

由多节点组成的无线传感器网络（W ireless Sensor Network， WSN）能够利用传感器节点（简称节点）间的相互协作来实现对监测区域的监测，已广泛应用于精密农业、防火救灾、雷达跟踪、目标定位等［1］。

在利用WSN进行参数估计时，估计算法可分为集中式和分布式。集中式算法要求网络中所有节点将观测数据发送到中心节点，并由中心节点完成数据的处理，因此中心节点负荷较重，易造成网络拥塞，容错能力差；分布式算法没有中心节点，通过节点之间的相互协作实现对参数的估计，与集中式算法相比，分布式算法潜在地节约了能量和通信资源，并且提高了算法的鲁棒性［25］-。

分布式算法是由不同的协作模式结合不同的自适应算法得到的。根据网络的拓扑结构，协作模式有增量（incremental）协作模式［3］、扩散（diffusion）协作模式［4］和一致协作模式［5］。在增量协作模式中，要求所有的节点组成一个环状循环结构，每个节点利用前一个邻居节点的信息来更新自身的估计值，然后把所得的估计值发送到下一个节点［3］，其中有学者分别针对各节点中的噪声不同［6］以及基于空间和网络的增量算法［7］进行了研究。这样的协作模式虽然需要的能量和通信量较小，易于实现，但对于由大量节点组成的网络来说，把所有节点设计成一个环状循环结构是不现实的。在扩散协作模式中，每个节点与其多个邻居节点进行实时通信，并利用自身和其邻居节点的数据来更新自身的估计值，然后把所得的估计值发送给其邻居节点，这样可以充分利用网络的联通性，且能够处理由大量节点组成的网络［810］-。而一致协作模式也是通过节点间的协作来达到参数估计的，但需要所有的节点都达到一致的效果，即收敛到相同的值，如基于一致的分布式最小均方算法［5］和能量检测算法［11］以及应用于目标追踪的Kalman算法［12］。由于一致协作模式需要每个节点都要收敛到相同值，这也限制了该协作算法在一些实际场景中的应用［13］。而扩散协作模式由于其简单的分布结构和较好的稳健性，得到广泛的关注，例如在稀疏结构当中的应用［14］和一些其它的改进算法［1517］-等。

目前的分布式估计算法一般都是假定网络处于安全信任的环境中，即认为所有节点的观测数据都是安全可靠的，不存在恶意攻击节点。而实际WSN中可能存在恶意攻击节点，它通过篡改自身的观测数据，以达到干扰或攻击整个网络的目的［12］。而被恶意篡改的数据参与数据融合时，将会影响参数估计的准确性，甚至无法实现对监测区域内参数的估计或动态目标跟踪［18］。如果能根据恶意节点的篡改程度，对其设置相应的信誉值，就能够在一定程度上减小恶意节点对整个网络参数估计的影响［19，20］。

本文针对WSN中恶意节点对参数估计的影响，提出基于信誉机制的扩散最小均方（Reputationbased diffusion Least Mean Square， R-d LMS）和扩散归一化最小均方（Reputation-based diffusion Normalized Least Mean Square， R-dNLMS）算法，它们根据节点对网络的贡献来设置其信誉值，以减小恶意节点对网络的影响。

2 扩散LMS算法

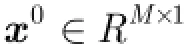
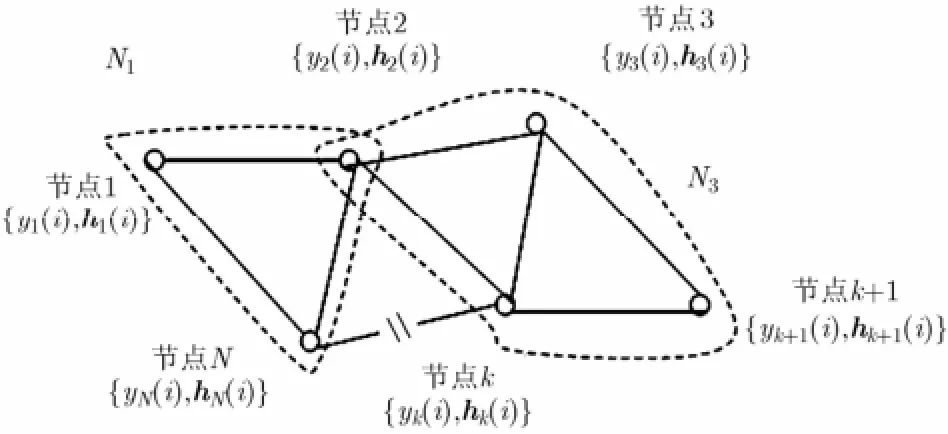
图1 由N个节点组成的WSN

观测数据的信号模型为

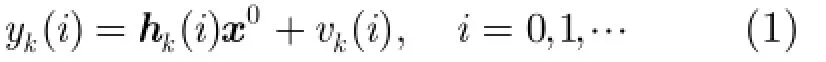
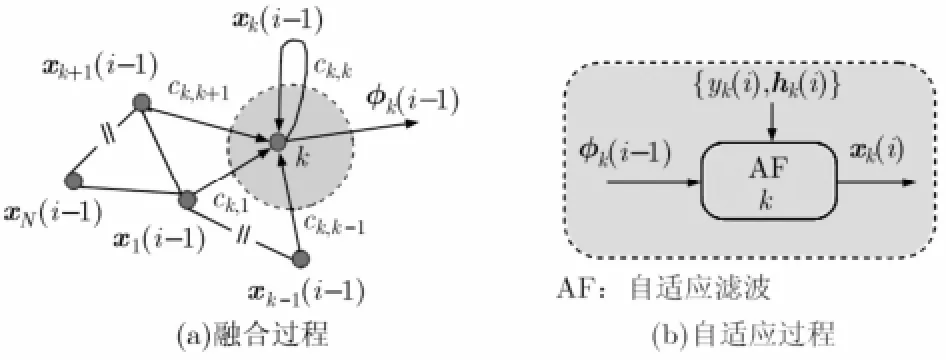
图2 扩散协作模式的网络结构

对应的扩散LMS（dLMS）算法可总结为

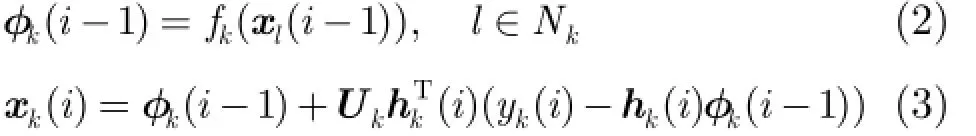
这些融合准则只适用于安全信任环境下的网络，若存在恶意节点，算法性能就会急剧恶化。为此，可根据节点对网络参数估计的贡献来动态地对其设置相应的信誉值，以减小恶意节点对整个网络性能的影响。

3 基于信誉机制的扩散算法

3.1 信誉值的确定

当WSN中存在恶意攻击节点时，恶意节点将根据其自身的攻击目的篡改其测量数据。假设恶意攻击节点相对总节点的个数较小，其数据篡改信号模型为

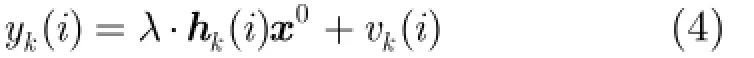
其中λ表示恶意节点对信号的篡改程度。λ=1该节点无攻击行为，而λ值偏离1越大，其攻击程度越强。

为了反映各节点对整个网络的贡献，利用节点估计值与其邻居节点估计值的均值之差（这里的差值表示差值的绝对值），根据其差值大小来对其设置相应的信誉值。

3.2 R-d LMS算法

表1 基于信誉机制的R-d LMS算法

3.3 R-dNLMS算法

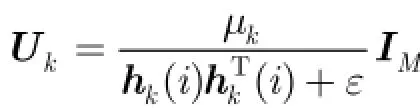
与R-d LMS算法相比，该算法能够有效避免梯度噪声放大的干扰， 因而具有更好的收敛性能。

3.4 算法收敛分析

本节借助范数理论来分析所提出算法的收敛性，首先给出分块矩阵最大范数的定义和一个引理。

表2 基于信誉机制的R-dNLMS算法

以上是对R-d LMS算法的收敛分析，而R-dNLMS算法是在R-dLMS算法的基础上进行了归一化处理［20］，其收敛性能分析与归一化LMS（NLMS）算法一致，此处不再赘述。

4 仿真分析

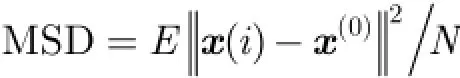
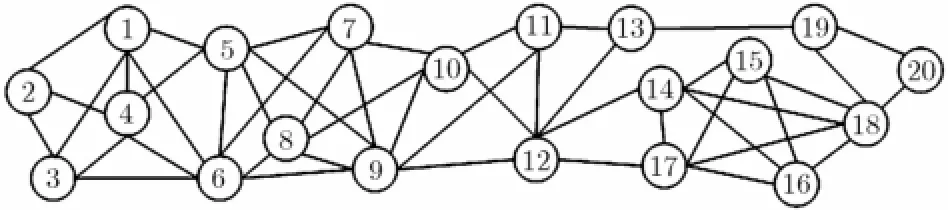
图3 网络拓扑结构

图4 给出了攻击程度不同时dLMS算法与所提出的R-dLMS算法仿真对比结果。由图4可知，当λ=1.0时，即网络中没有恶意攻击节点时，R-dLMS算法的偏差曲线几乎和dLMS算法重合，都是在迭代200次时达到-41 dB左右的平稳状态，说明了所提出的R-dLMS算法的有效性；当λ=0.5时，R-dLMS算法的偏差达到了-37 dB，比dLMS算法降低了11 dB；当λ=3.0时， R-dLMS算法偏差达到-29 dB左右，比dLMS算法降低了14 dB。而此时R-dLMS算法对节点11和其邻居节点设置的信誉值如图5所示，当R-d LMS算法达到平稳状态时，给恶意节点11设置的信誉值为0.06左右，而其邻居节点的信誉值在0.23上下波动，是恶意节点的信誉值的4倍左右。由对比分析可知，当存在恶意攻击节点时，R-dLMS算法能够判别出恶意节点并对其设置相应小的信誉值，从而减小恶意节点对参数估计的影响，提高算法的性能。

图6给出了在随迭代次数增加的过程中，出现不同攻击程度时dLMS与R-dLMS算法的对比仿真结果。由图6可知，当迭代200次左右时d LMS和R-d LMS算法的偏差都达到了-41 dB的平稳状态；当迭代300次时，出现了恶意攻击且λ=2.0， dLMS算法性能急剧恶化，而R-d LMS算法的偏差水平达到了-35 dB，比d LMS算法小了12 dB左右；当迭代500次时，恶意节点攻击程度增加至λ=3.0，dLMS算法性能进一步恶化，而R-d LMS算法的偏差达到了-30 dB，比dLMS算法小了13 dB；当迭代800次时，恶意攻击消失，d LMS和R-dLMS算法都开始好转，dLMS算法经过迭代100次左右达到平稳，而R-dLMS经过迭代近50次就达到了平稳状态。

同时，R-d LMS算法对节点11及其邻居节点设置的信誉值如图7所示，当迭代100次左右时，各节点的信誉值都在0.200左右的稳定状态，说明各节点对整个网络参数估计的贡献基本相等；当迭代300次时，节点11的信誉值由0.215变为0.075左右，而其邻居节点的信誉值在不同程度上有所增加；当迭代500次时，节点11的信誉值减小至0.062左右，说明节点11又实施了进一步的攻击；当迭代800次时，所有节点的信誉值又回到了0.200左右，说明恶意攻击消失。由此可知，当迭代过程中出现恶意节点时，R-dLMS算法也能够判别出恶意节点并对其设置相应小的信誉值，从而减小对整个网络的攻击影响。

图9给出了扩散归一化LMS（dNLMS）算法和基于信誉值的R-dNLMS算法对比仿真结果。由图9可知，当1.0λ=时，即没有恶意攻击节点时，R-dNLMS算法能够达到dNLMS算法的性能水平，偏差都能达到-43 dB，也进一步说明了所提出算法的有效性；当0.5λ=时，R-dNLMS算法偏差达到了-39 dB，比dNLMS算法的偏差降低了9 dB左右；当3.0λ=时，R-dNLM S算法的偏差达到了-33 dB，比dNLMS算法降低了14 dB左右。同时，R-dNLMS算法给节点11及其邻居节点设置的信誉值和图5的结果非常相近，并且R-dNLMS算法也有与图6～图8相似的仿真结果，此处不再赘述。这也说明了所提出的基于信誉机制的扩散算法能够有效地分辨出恶意节点，并给其设置相应小的信誉值，从而减小恶意节点对整个网络的影响。

图4 λ值不同时，R-d LMS算法与d LMS算法对比

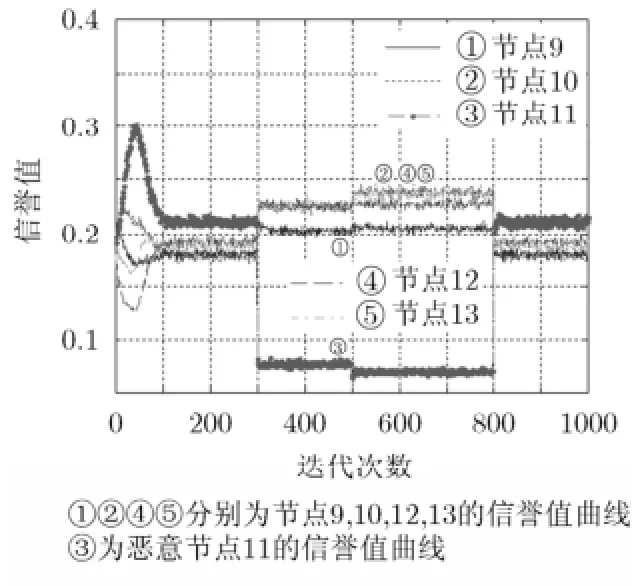
图7 R-d LMS对节点11及其邻居节点设置的信誉值

图8 节点6， 11， 20分别为 恶意节点时算法对比

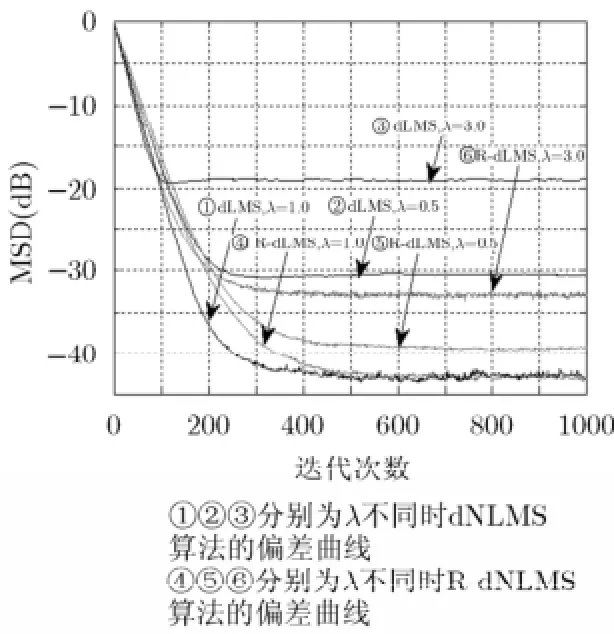
图9 λ值不同时，R-dNLMS算 法与dNLMS算法对比

图5 当3.0λ=时，恶意节点 11和其邻居节点的信誉值

图6 迭代过程中出现恶 意攻击时算法对比

从图4和图9的对比中，可以看出，当λ=1.0时，即网络处于安全的环境中，R-dLMS算法和R-dNLMS算法都能分别达到d LMS算法和dNLMS算法的性能水平；当存在恶意节点且3.0λ=时，R-d LMS算法和R-dNLMS算法偏差分别达到-29 dB和-33 dB，与dLMS和dNLMS算法相比，所提出的算法都能够大幅度地提升算法的性能。同时，R-dNLMS算法比R-dLMS算法有更好的稳定性，偏差也更小，算法性能更优。

5 结束语

本文主要对处于非安全环境中的无线传感器网络进行研究，当网络中存在恶意攻击节点时，恶意节点篡改其观测数据，并参与数据融合，影响参数估计的准确性，甚至无法实现对监测区域的参数估计。本文利用节点估计值与其邻居节点估计值的均值之差，根据其差值大小来反映节点对整个网络的贡献，并对其设置相应的信誉值，提出基于信誉机制的R-dLMS算法和R-dNLMS算法，该算法能够使恶意节点的信誉值最小，非恶意节点的信誉值相对较大，从而减小恶意节点对网络攻击的影响。仿真结果验证了算法的正确性和有效性，并且R-dNLMS算法在R-dLMS算法的基础上，算法性能在一定程度上又得到了进一步的提升。而该算法与信道环境相关的研究将是下一步的重点工作。

［1］ Estrin D， Girod L， Pottie G， et al.. Instrumenting the worldw ith w ireless sensor networks［C］. Proceedings of the IEEE International Con ference on A coustics， Speech， and Signal Processing （ICASSP，01）， Salt Lake City， USA， 2001， 4: 2033-2036.

［2］ Sayed A H and Lopes C G. Distributed p rocessing over adaptive networks［C］. Proceedings of the 9th International Sym posium on Signal Processing and Its Applications（ISSPA）， Sharjah， UAE， 2007: 1-3.

［3］ Lopes C G and Sayed A H. Incremental adaptive strategies over distributed networks［J］. IEEE Transactions on Signal Processing， 2007， 55（8）: 4064-4077.

［4］ Lopes C G and Sayed A H. Diffusion least-mean squares over adaptive networks: formulation and performance analysis［J］. IEEE Transactions on Signal Processing， 2008， 56（7）: 3122-3136.

［5］ Schizas I D， M ateos G， and Giannakis G B. D istributed LMS for consensus-based in-network adaptive processing［J］. IEEE Transactions on Signal Processing， 2009， 57（6）: 2365-2382.

［6］ Khalili A， Tinati M A， and Rastegarnia A. Steady-state analysis of incremental LMS adaptive networks w ith noisy links［J］. IEEE Transactions on Signal Processing， 2011， 59（5）: 2416-2421.

［7］ Cattivelli F S and Sayed A H. Analysis of spatial and incremental LMS p rocessing for distributed estimation［J］. IEEE Transactions on Signal Processing， 2011， 59（4）: 1465-1480.

［8］ Khalili A， T inati M A， Rastegarn ia A， et al.. Steady-state analysis of diffusion LM S adaptive networks w ith noisy links［J］. IEEE Transactions on Signal Processing， 2012， 60（2）: 974-979.

［9］ Zhao X and Sayed A H. Combination weights for diffusion strategies w ith im perfect in formation exchange［C］. Proceedings of the IEEE International Conference on Communications （ICC）， Ottawa， Canada， 2012: 398-402.

［10］ Li C， Shen P， Liu Y， et al.. Diffusion information theoretic learning for distributed estimation over network［J］. IEEE Transactions on Signal Processing， 2013， 61（16）: 4011-4024.

［11］ 王晓侃， 卢光跃， 包志强， 等. 一种新的分布式协作能量检测算法［J］. 电讯技术， 2012， 52（9）: 1480-1485. Wang Xiao-kan， Lu Guang-yue， Bao Zhi-qiang， et al.. A novel distributed cooperative energy detection algorithm［J］. Telecommunication Engineering， 2012， 52（9）: 1480-1485.

［12］ 白辉， 卢光跃， 王晓侃. 非信任环境中一致卡尔曼滤波的数据融合算法［J］. 西安邮电学院学报， 2012， 17（5）: 10-14. Bai Hui， Lu Guang-yue， and Wang Xiao-kan. Data fusion algorithm based on consensus Kalman filter in untrustworthy environment［J］. Journal of Xi，an University of Posts and Telecommunications， 2012， 17（5）: 10-14.

［13］ Cattivelli F S and Sayed A H. Distributed detection over adaptive networks using diffusion adaptation［J］. IEEE Transactions on Signal Processing， 2011， 59（5）: 1917-1932.

［14］ D i Lorenzo P and Sayed A H. Sparse distributed learn ing based on diffusion adaptation［J］. IEEE Transactions on Signal Processing， 2013， 61（6）: 1419-1433.

［15］ 聂文梅， 卢光跃. 无线传感器网络中丢包扩散卡尔曼算法的改进［J］. 西安邮电学院学报， 2013， 18（4）: 9-12. Nie W en-m ei and Lu Guang-yue. Im proved d iffusion Kalm an algorithm w ith packet-d ropping in w ireless sensor networks［J］. Journal of Xi，an University of Posts and Telecommunications，2013， 18（4）: 9-12.

［16］ 陈文晓， 卢光跃， 黄庆东. 改进的分布式扩散符号LMS算法［J］. 电讯技术， 2013， 53（12）: 1580-1585. Chen Wen-xiao， Lu Guang-yue， and Huang Qing-dong. An im proved distributed diffusion sign-LMS algorithm［J］. Telecommunication Engineering， 2013， 53（12）: 1580-1585.

［17］ Li J， Chen W， Kang S， et al.. A diffusion-based distributed collaborative energy detection algorithm for spectrum sensing in cognitive radio［J］. Comm unications and Network，2013， 5（3）: 276-279.

［18］ 冯景瑜， 卢光跃， 包志强. 认知无线电安全研究综述［J］. 西安邮电学院学报， 2012， 17（2）: 47-52. Feng Jing-yu， Lu Guang-yue， and Bao Zhi-qiang. A survey on cognitive radio security［J］. Journal of Xi，an University of Posts and Telecommunications， 2012， 17（2）: 47-52.

［19］ de Pau la A and Panazio C. Analysis of distributed parameter estimation in WSN w ith unreliable nodes［C］. Proceedings of the International Sym posium on W ireless Communication System s， Paris， France， 2012: 116-120.

［20］ Lopes C G. D iffusion adaptive networks w ith changing topologies［C］. Proceedings of the IEEE International Conference on Acoustics， Speech and Signal Processing， Las Vegas， USA， 2008: 3285-3288.

［21］ Xiao L and Boyd S. Fast linear iterations for distributed averaging［J］. System s & Control Letters， 2004， 53（1）: 65-78.

［22］ Olfati-Saber R and Murray R M. Consensus problem s in networks of agents w ith sw itching topology and timedelays［J］. IEEE Transactions on Automatic Control， 2004，49（9）: 1520-1533.

［23］ Jadbabaie A， Lin J， and M orse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules［J］. IEEE Transactions on Autom atic Control， 2003， 48（6）: 988-1001.

［24］ Takahashi N， Yam ada I， and Sayed A H. D iffusion least-m ean squares w ith adaptive comb iners: form ulation and performance analysis［J］. IEEE Transactions on Signal Processing， 2010， 58（9）: 4795-4810.

［25］ Xie S L and Li H R. Distributed LMS w ith limited data rate［J］. Electronics Letters， 2011， 47（9）: 541-542.

卢光跃： 男，1971年生，博士，教授，博士生导师，研究方向为现代移动通信中信号处理.

陈文晓： 男，1985年生，硕士生，研究方向为无线传感器网络中的数据融合.

黄庆东： 男，1977年生，博士，副教授，研究方向为自适应信号处理及分布式算法.

Distributed Diffusion Least M ean Square A lgorithm Based on the Reputation M echanism

Lu Guang-yue Chen Wen-xiao Huang Qing-dong
（National Engineering Laboratory for W ireless Security， X i’an University of Posts and Telecommunications， Xi’an 710121， China）

To deal with the problem of signal estimation for W ireless Sensor Networks （WSN） in a untrustworthy environment where malicious nodes tamper the measured data， two reputation-based algorithm s， that are，Reputation-based diffusion Least Mean Square （R-d LMS） algorithm and Reputation-based diffusion Normalized Least Mean Square （R-dNLMS） algorithm， are proposed. The p roposed algorithms cou ld assign the app rop riate reputation value to each node according to its contribution to the whole network， and m inim ize the reputation value of malicious nodes to lower the im pact of malicious nodes in the network. Simulation resu lts show that the proposed algorithms can greatly im prove the performance com pared w ith the one w ithout reputation value， and the perform ance of R-dNLMS algorithm has been further im proved based on R-d LMS algorithm.

W ireless Sensor Network （W SN）； M alicious attack； Distributed； Diffusion Least M ean Square （dLMS）；Repu tation value

TP393； TN911.7

： A

：1009-5896（2015）05-1234-07

10.11999/JEIT140851

2014-06-26收到，2014-11-18改回

国家自然科学基金（61271276， 61301091），陕西省国际合作项目（2013KW 01-03），工业和信息化部通信软科学项目（2014R33）和陕西省自然科学基金（2014JM 8299）资助课题

*通信作者：卢光跃 tonylugy@163.com