一种稳健的机载非正侧视阵雷达杂波抑制方法

同亚龙 王 彤文 才 吴建新

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

一种稳健的机载非正侧视阵雷达杂波抑制方法

同亚龙 王 彤*文 才 吴建新

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

非正侧视阵列构型会导致机载雷达回波数据非均匀，从而严重削弱传统空时自适应处理算法的杂波抑制性能。针对此问题，该文提出一种对阵元误差稳健的非均匀杂波抑制方法。该方法首先根据雷达系统参数等先验信息构造杂波表示基；然后在考虑阵元误差下对待检测单元数据进行迭代的最小二乘拟合，文中推导出了该问题的闭式解；最后对拟合后的剩余数据进行脉冲多普勒处理以及恒虚警检测。该方法不需要训练样本，且能够在没有俯仰自由度的情况下对机载非正侧视阵雷达的非均匀杂波进行有效抑制。仿真结果验证了该方法的有效性。

机载雷达；非正侧视阵；非均匀杂波；杂波抑制；空时自适应处理

1 引言

机载预警雷达在接收目标回波信号的同时，会不可避免地受到复杂强地杂波的影响。如何从极强的杂波背景中对运动目标进行有效检测始终是机载预警雷达信号处理的核心任务，因此杂波成为其必须解决的首要问题。空时自适应处理（Space-Time Adap tive Processing， STAP）技术能够从空间和时间两维上同时区分运动目标和杂波，可以在很大程度上改善机载预警雷达的杂波抑制及动目标检测性能，特别是对低速目标以及被旁瓣杂波所遮蔽的弱小目标的检测更为有效，因而得到了广泛的关注［13］-。然而杂波信号统计特性往往是无法预知的，STAP需要选取待检测单元（Cell Under Test， CUT）附近的回波数据作为训练样本对其进行估计。为获得较优的STAP性能（相对于最优处理的性能损失不超过3 dB），所需要的训练样本数不应少于系统自由度的两倍［4］。这里假设所选用的训练样本与待检测单元数据满足独立同分布（Independent and Identically D istributed， IID）条件，即这些训练样本是均匀的且能够反映CUT数据的统计特性。然而，由于实际场景中存在多变的地表类型、植被覆盖以及孤立干扰等情况，机载雷达通常都工作在非均匀杂波环境中［5］；另外，当雷达天线非正侧视安置时，近程回波会具有非常明显的距离依赖性［68］-。这些因素都会导致机载雷达回波数据非均匀，使得上述假设所要求的IID样本条件很难满足，STAP的杂波抑制性能受到很大程度的削弱。

对于非均匀环境造成的STAP性能下降问题，目前通常采用的解决办法是在自适应信号处理前级联有效的非均匀检测器（Non-Homogeneity Detector， NHD），对数据均匀性做出判断，从而剔除有损自适应算法性能的非均匀样本数据［912］-。这类算法能够在一定程度上提高非均匀环境下的检测性能，但当环境非均匀性严重时，NHD需要剔除大量奇异样本，使得可用来进行自适应权值训练的样本数变少甚至不足，STAP算法性能得不到有效提高，另外，这类算法大都关注的是如何更好地去除非均匀的训练样本，而无法对CUT内的孤立杂波进行有效抑制。针对雷达非正侧视安置所带来的非均匀杂波抑制问题的研究也较多，比较典型的解决方法有多普勒补偿［13，14］、角度多普勒补偿［15，16］、配准补偿［17，18］等算法，但当雷达发射中高脉冲重复频率信号时，会发生距离模糊现象，这些补偿类算法不能对多次模糊的回波数据进行一致补偿，即在对近程杂波的距离依赖性进行补偿的同时会造成模糊的远程平稳杂波出现新的非均匀性。除此之外，3维STAP方法［19］利用接收系统具有的俯仰维自由度，理论上也可以对非正侧视阵雷达的近程非均匀杂波进行有效抑制，但由于系统自由度的增加，其运算量显著增大，且对IID样本数据的需求也更大，这在实际应用中很难满足。另外，带有俯仰预滤波处理的子阵合成算法［20］在不存在阵元误差影响下可以有效抑制近程非均匀杂波，但阵元误差在实际情况中是不可避免的，算法性能因此受到很大程度地削弱。

针对以上问题，本文提出了一种对阵元误差稳健的机载非正侧视阵雷达非均匀杂波抑制方法。对于均匀线性阵列天线或者列合成后的线性子阵系统，由于缺乏俯仰自由度，不能直接对近程非均匀杂波进行有效抑制。在这种情况下，本文方法首先根据机载雷达系统参数以及平台运动状态等先验信息构造杂波表示基，然后在考虑阵元误差影响下对CUT数据进行迭代的最小二乘拟合，最后对拟合后的剩余数据进行常规的脉冲多普勒处理以及单元平均恒虚警率（Cell-Averaging Constant False A larm Rate， CA-CFAR）检测。文中推导出了所涉及到的最小二乘问题的闭式解，大大减少了所提算法的运算复杂度。仿真实验验证了本文方法的有效性。

2 信号模型与杂波特性

机载雷达的几何构型如图1所示。假定雷达天线为非正侧视均匀线阵，载机以速度v沿平行于Y轴正方向的水平方向飞行，高度为h；雷达阵面由间距为d的N个阵元组成，阵面偏置角（阵面轴向与速度矢量的夹角）为α；雷达工作波长为λ，脉冲重复频率为 fr，一个相干处理时间内的脉冲数为M。

图1 机载雷达阵面与杂波几何关系

若杂波散射体相对于天线阵面的方位角和俯仰角分别为θ和φ，ψ是其对应的空间锥角，满足cos（ψ）= cos（θ） cos （φ），则该散射体回波的归一化多普勒频率为

由Ward模型［1］可知，第l个采样距离单元所接收到的杂波回波信号是由各次模糊距离门内不同方位角处散射体回波的线性叠加，因而可以表示为

由于同一距离环中不同杂波散射体之间是互不相关的，因此第l个采样距离单元的回波数据所对应的协方差矩阵可表示为

为了防止光束在球面镜的外表面与内表面之间干涉，球面反射镜的外表面镀99%的增透膜.若球面反射镜和微悬臂的反射率分别为R1，R2，球面镜与微悬臂的距离为L，即半球面F-P腔腔长，则相邻光束之间的光程差为4L，位相差为

当阵列天线不存在误差时，天线上的每个阵元具有一致的幅相特性，此时由式（2）-式（5）所给出的信号模型可以很好地表征机载雷达回波数据中的杂波信号。但在实际阵列天线中，受机械加工等因素的影响，不可避免地存在着各种误差，这也就意味着式（4）所采用的理想阵列流型已不再合适，此时需要考虑误差对阵列天线的影响。本文主要考虑阵元误差这一典型情况［21，22］，其误差模型可以表示为

其中diag（·）表示对角化操作， IM表示M维的单位阵。这样，在存在阵元误差影响时，杂波的真实空时导向矢量就需要用式（8）的锥削矩阵对式（3）进行修正，即

3 非均匀杂波抑制方法

由上述杂波特性分析可以看出，非正侧视阵雷达系统的杂波2维谱随距离的变化而变化。传统STAP方法需要选取CUT附近一段距离范围内的样本数据进行自适应权值的训练，而非正侧视阵杂波的这种距离依赖性会导致STAP杂波抑制凹口变宽，降低算法对低速运动目标的检测性能。另外，由于无法估计CUT内孤立杂波的统计特性，STAP不能对其进行充分抑制从而造成大量虚警。本节给出一种对阵元误差稳健的机载非正侧视阵雷达非均匀杂波抑制方法，主要包括杂波表示基的构造、杂波与误差的迭代估计两部分。

3.1 构造杂波表示基

式（6）所给出的杂波协方差矩阵可以写成

其中svd（·）表示奇异值分解操作，U和V分别表示Sl的左、右奇异向量矩阵，Σ为奇异值矩阵。

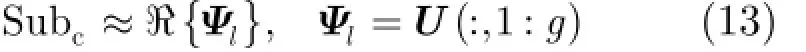
其中η∈［0，1］，越接近于1逼近质量越高。这样可以通过设置有效秩g为满足η≥η0的最小整数来保证杂波子空间的逼近效果，其中η0为接近于1的阈值，例如η0= 0.999等。

在考虑存在阵元误差影响时，将式（9）中修正的杂波空时导向矢量代入到上述计算可得新的杂波表示基矩阵为

对于杂波表示基的构造，这里有两点需要进行说明。一是距离模糊数 Nr的设定，由于非正侧视阵的远程杂波逐渐趋于平稳，高次模糊距离门杂波分量的角度多普勒谱几乎重合，其相应的空时信号流型近似一致；另一方面，远程杂波信号的回波功率随距离的衰减非常严重。因此lS表达式中rN的设定可根据实际需要进行调整，这样就大大降低了高维矩阵奇异值分解所带来的运算复杂度。二是本部分杂波表示基的构造可以离线完成，即在已知阵列响应及平台运动参数的情况下，可在实时数据处理之前计算并存储算法所要用到的杂波表示基，有助于算法具有更好的实时性。

3.2 迭代估计杂波与误差

用式（15）所获得的杂波表示基矩阵ˆlΨ对第l个采样单元数据lx进行最小二乘拟合，可通过求解式（16）的优化问题完成

当阵元误差已知时，式（16）可转化为

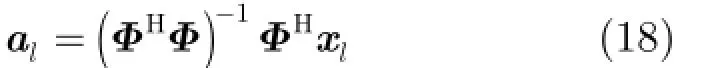
当拟合系数已知时，式（16）的目标函数可变形为

也就是说，原N维的优化问题可以分解为N个1维的优化问题，其中每一个子优化问题都是一个超定的最小二乘问题，存在唯一的最小均方误差解，即

本文算法的详细处理流程在图2中给出。另外需要说明的是，本文采用的是全维处理方式，当雷达系统空时自由度过大时，本文算法也可很容易推广到空域、时域或空时域降维处理方式。

4 仿真实验

本文按照表1所给出的雷达系统参数进行仿真实验。为了验证本文算法对非正侧视阵杂波的抑制效果，实验以前视阵情况（即α=-90o）为例进行说明。杂波数据按照W ard模型仿真产生，其能量受方向图及距离联合调制。阵列天线单阵元单脉冲回波数据的杂噪比为40 dB，且存在10%的幅度误差以及6o的相位误差。另外，为了更好地反映本文算法相对于已有算法在非均匀环境中的性能优势，仿真数据中注入了5个运动目标信号以及4个强的旁瓣孤立杂波点信号，这些信号的空域流型也存在着相同的阵元误差，其具体参数如表2所示。所注入的强杂波点信号可认为来自于具有比背景杂波强得多的雷达后向散射系数的地面散射体，如桥梁、铁塔、角反射器等，有助于增强仿真数据的非均匀性。

图3给出的是仿真数据的常规脉冲多普勒处理结果，从图中可以看出近程杂波具有很强的距离非均匀性，这种非均匀性往往使得传统STAP方法不能获得足够的IID训练样本，从而无法对CUT内的杂波统计特性进行有效估计，造成非正侧视阵情况下的杂波抑制及运动目标检测性能的严重下降。图中标注出了所注入的运动目标及孤立杂波点信号的位置，其中运动目标1和目标2被近程弯曲杂波所淹没，运动目标4为靠近主瓣杂波多普勒的弱小目标。

图2 算法流程图

表1 雷达系统参数

表2 注入信号参数

图3 脉冲多普勒处理结果

下面通过两组实验结果对本文算法的有效性进行说明。实验中选作性能对比的是两种比较典型的传统STAP方法［1］：扩展因子化法（Ex tended Factored App roach， EFA）和联合域局域化（Joint Domain Localized， JDL）方法。图4给出了EFA，JDL以及本文算法对仿真数据进行滤波处理后的距离多普勒结果，从图4中可以看出EFA和JDL由于无法充分估计近程非均匀杂波的统计特性因而不能对其进行有效的自适应抑制，而经过本文算法处理后上述非均匀杂波大部分都被有效滤除。图5给出的是对3种方法的滤波输出进行CA-CFAR检测的目标检测结果。在图5（a）和图5（b）中可以看到，STAP处理由于无法获得孤立杂波点信号的训练样本，因此无法对其进行估计和抑制，4个强杂波点信号在CA-CFAR检测后表现为虚警；强杂波点的存在也抬高了恒虚警检测门限，造成对其附近运动目标（如目标3和目标5）的漏警；运动目标1和目标2仍然被湮没在较强的近程剩余杂波中而无法得到有效检测；靠近主杂波的弱小目标4在两种STAP方法处理中也同样没有得到检测。从图5（c）可以看到，经本文算法处理后，4个强杂波点信号均被有效滤除，而所有运动目标也都得到了检测。

图6给出了EFA， JDL以及本文算法的检测概率曲线比较。实验选取第21号到30号多普勒通道、第201号到400号距离门范围内的回波数据做总共2000次的蒙特卡洛实验，虚警概率设置为0.01。从图6（a）中可以看出，EFA和JDL的检测性能比较接近，而本文算法的检测性能则远好于这两种STAP方法，在检测概率为0.8时，有超过4 dB的性能优势。另外，本文算法对先验信息的依赖性较强，实验中也对系统参数存在误差的情况进行了检查。图6（b）和6（c）中分别给出的是实际雷达系统中较为常见的偏航角误差及载机速度误差情况下算法的检测性能比较，可以看出在偏航角存在0.1°， 0.5°及1°误差时对算法性能影响不大；在存在较小的载机速度误差时本文算法性能会受到一定损失，随着速度误差增大算法性能损失会加大。但从公开的国内外器件性能指标及发展趋势来看，机载雷达系统参数的测量误差会控制在一定范围之内并且精度会越来越高，因此本文算法仍然具有很高的实用价值。

图4 杂波抑制后的距离多普勒图

图5 目标检测结果

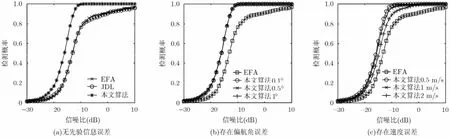
图6 检测曲线比较

5 结论

本文提出了一种机载雷达非正侧视阵情况下的非均匀杂波抑制方法。该方法充分利用了雷达系统参数及平台运动状态等先验信息，通过离线构造杂波表示基，可以大大提高算法的实时性；无需训练样本，不用估计杂波统计特性，适用于极度非均匀回波数据的杂波抑制问题；对阵元误差稳健，提高对运动目标的检测性能；可以在没有俯仰自由度的情况下对非正侧视阵杂波进行有效抑制。仿真结果验证了本文算法的有效性。

［1］ Ward J. Space-time adaptive p rocessing for airborne radar［R］. Lincoln Laboratory， M IT， 1994.

［2］ K lemm R. Princip les of Space-T ime Adaptive Processing［M］. London: the Institution of Electrical Engineers， 2002: 117-149.

［3］ Brennan L E and Reed I S. Theory of adaptive radar［J］. IEEE Transactions on Aerospace and Electronic Systems，1973， 9（1）: 237-252.

［4］ Reed I S， M allett J D， and B rennan L E. Rap id convergence rate in adaptive arrays［J］. IEEE Transactions on Aerospace and Electronic System s， 1974， 10（4）: 853-863.

［5］ Melvin W L. Space-time adaptive radar performance in heterogeneous clutter［J］. IEEE Transactions on Aerospace and Electronic System s， 2000， 36（2）: 621-633.

［6］ Wang Yong-liang， Duan Ke-qing， and Xie Wen-chong. Cross beam STAP for nonstationary clutter supp ression in airborne radar［J］. International Journal of An tennas and Propagation，2013， ID: 276310.

［7］ 文珺， 史林， 廖桂生. 一种机载非正侧视阵雷达近程杂波对消方法［J］. 系统工程与电子技术， 2013， 35（10）: 2069-2073. Wen Jun， Shi Lin， and Liao Gui-sheng. Short-range clutter elim ination method for non-side looking airborne radar［J］. System s Engineering and Electronics， 2013， 35（10）: 2069-2073.

［8］ 王杰， 沈明威， 吴迪， 等. 基于主瓣杂波高效配准的机载非正侧视阵雷达STAP算法研究［J］. 雷达学报， 2014， 3（2）: 235-240. Wang Jie， Shen M ing-wei， Wu Di， et al.. An efficient STAP algorithm for nonsidelooking airborne radar based on m ainlobe clutter com pensation［J］. Journal of Radars， 2014，3（2）: 235-240.

［9］ Yang Xiao-peng， Liu Yong-xu， and Long Teng. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-tim e adaptive processing［J］. IET Radar， Sonar & Navigation， 2013， 7（1）: 47-54.

［10］ Chen Si-jia， Kong Ling-jiang， and Yang Jian-yu. Target detection for heterogeneous cyclostationary sea clutter［J］. Circuits， Systems， and Signal Processing， 2014， 33（3）: 959-971.

［11］ Aubry A， De M aio A， Pallotta L， et al.. Median matrices and their application to radar training data selection［J］. IET Radar， Sonar & Navigation， 2014， 8（4）: 265-274.

［12］ Zaimbashi A. An adaptive cell averaging-based CFAR detector for interfering targets and clutter-edge situations［J］. D igital Signal Processing， 2014， 31: 59-68.

［13］ Borsari G. M itigating effects on STAP p rocessing caused by an inclined array［C］. Proceedings of the IEEE National Radar Conference， Dallas， USA， 1998: 135-140.

［14］ K reyenkam p O and K lemm R. Doppler com pensation in forward-looking STAP radar［J］. IEE Proceedings of Radar，Sonar & Navigation， 2001， 148（5）: 253-258.

［15］ Himed B， Zhang Yu-hong， and Hajjari A. STAP w ith angle-Doppler com pensation for bistatic airborne radars［C］. Proceedings of the IEEE Radar Conference， California， USA，2002: 311-317.

［16］ Colone F. Spectral slope-based approach for m itigating bistatic space-time adaptive p rocessing clutter dispersion［J］. IET Radar， Sonar & Navigation， 2011， 5（5）: 593-603.

［17］ Ries P， Lapierre F D， Lesturgie M， et al.. Hand ling partially calibrated con formal antenna arrays in range-dependence com pensation for airborne bistatic space-time adaptive processing radar［J］. IET Radar， Sonar & Navigation， 2009，3（4）: 373-383.

［18］ Lapierre F D， Ries P， and Verly J G. Foundation for m itigating range dependence in radar space-time adaptive processing［J］. IET Radar， Sonar & Navigation， 2009， 3（1）: 18-29.

［19］ Corbell P M and Hale T B. 3-dimensional STAP performance analysis using the cross-spectral metric［C］. Proceedings of the IEEE Radar Conference， Philadelphia， USA， 2004: 610-615.

［20］ Meng Xiang-dong， Wang Tong， Wu Jian-xin， et al.. Shortrange clu tter suppression for airborne radar by utilizing prefiltering in elevation［J］. IEEE Geoscience and Rem ote Sensing Letters， 2009， 6（2）: 268-272.

［21］ Li Jian-feng， Zhang Xiao-fei， and Gao Xin. A joint scheme for angle and array gain-phase error estimation in bistatic M IMO radar［J］. IEEE Geoscience and Remote Sensing Letters， 2013，10（6）: 1478-1482.

［22］ Cao Sheng-hong， Ye Zhong-fu， Hu Nan， et al.. DOA estimation based on fourth-order cumulants in the presence of sensor gain-phase errors［J］. Signal Processing， 2013， 93（9）: 2581-2585.

同亚龙： 男，1987年生，博士生，研究方向为阵列信号处理、空时自适应信号处理以及地面运动目标检测.

王 彤： 男，1974年生，教授，研究方向为机载雷达运动目标检测、合成孔径雷达成像等.

文 才： 男，1986年生，博士生，研究方向为阵列信号处理、空时自适应信号处理以及地面运动目标检测.

吴建新： 男，1982年生，副教授，研究方向为空时自适应信号处理、雷达成像以及动目标检测等.

A Robust Clutter Suppression M ethod for A irborne Non-sidelooking Radar

Tong Ya-long Wang Tong Wen Cai Wu Jian-xin
（National Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071， China）

Non-sidelooking array configuration leads to heterogeneous airborne radar echo data， it degrades seriously the clutter suppression performance of the traditional Space-Time Adap tive Processing （STAP）algorithm s. To solve this p rob lem， a heterogeneous clu tter suppression m ethod， which is robust to array error， is proposed. Firstly， a clutter rep resentation basis is constructed based on a priori information such as system parameters. Then， the test data is fitted in an iterative least square manner with consideration of array error， and the closed-form solution is derived and utilized here. Finally， pulse Doppler p rocessing and constant false alarm detection are conducted on the residual data. The proposed method does not need any training samp le and can effectively suppress the heterogeneous clutter for airborne non-sidelooking radar w ithout elevation degree of freedom. Simu lation results verify the validity of the p roposed m ethod.

Airborne radar； Non-sidelooking array； Heterogeneous clutter； Clutter suppression； Space-Time Adaptive Processing （STAP）

TN959.73

： A

：1009-5896（2015）05-1044-07

10.11999/JEIT141222

2014-09-19收到，2014-12-11改回

国家自然科学基金（61372133， 61471285）资助课题*通信作者：王彤 twang@mail.xidian.edu.cn