一种基于先验信息的机载M IMO雷达发射方向图设计方法

施君南 纠 博刘宏伟 王 旭

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

一种基于先验信息的机载M IMO雷达发射方向图设计方法

施君南 纠 博*刘宏伟 王 旭

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

在非均匀杂波背景下，针对旁瓣杂波抑制问题，该文提出一种基于先验信息的机载多输入多输出（M IMO）雷达发射方向图设计方法。该方法利用目标和杂波在空域和多普勒域的2维先验信息，以最大化雷达空时匹配滤波后的输出信杂噪比（SCNR）为准则，建立关于发射信号相关矩阵的优化代价函数，并采用半正定规划（SDP）方法进行求解。仿真表明，在非均匀杂波背景下，采用该文方法优化设计的发射方向图可有效提高空时2维匹配滤波后的输出信杂噪比。

机载雷达；多输入多输出雷达；信杂噪比；发射方向图；空时2维匹配滤波

1 引言

传统机载雷达在接收端采用空时自适应处理技术（Space-Tim e Adaptive Processing， STAP）［1］，该技术通过估计杂波的相关矩阵，设计接收滤波器来抑制杂波，提高信杂噪比。然而在复杂环境下，杂波空域非均匀分布的特性使得传统处理方法存在杂波的相关矩阵估计样本不足的问题，这个问题导致接收端的杂波抑制性能变差。因此，如何在复杂杂波背景下针对机载平台进行杂波抑制已成为机载雷达探测的重点和难点问题。在传统机载雷达中，发射波形通常是预先设定的，不能根据具体的环境自适应地改变发射波形，这会显著降低雷达系统对环境的适应能力。在复杂的战场环境下，基于先验信息的认知雷达［24］-发射波形优化技术可以根据环境和目标的先验信息主动地改变发射波形，以实现发射波形优化的目的。由于它可以极大地提升系统的灵活性，充分挖掘雷达在发射端的自由度，有望大幅提升雷达接收回波的质量。基于先验信息的发射波形优化技术近年来受到了广泛的关注，并被认为是雷达发展的重要方向。

相比于相控阵雷达，集中式多输入多输出（M IMO）雷达［5，6］各个发射天线可以发射不同信号，具有更高的发射自由度，可以为基于先验信息的认知技术提供良好的平台。因此，结合M IMO雷达，研究基于先验信息的机载认知发射技术对于提升机载雷达灵活性，改善机载雷达在复杂杂波背景下的杂波抑制、目标探测性能具有重要的意义。

总而言之，机载认知发射技术具有如下优势，一是以M IMO雷达技术为载体，机载认知发射技术可以针对不同的杂波环境，设计出特定的发射方向图，具有环境适应能力；二是有效地利用发射端的资源，减轻接收端的工作负荷，为接收端节约了自由度；三是较相控阵雷达具有更高的发射自由度和更好的杂波抑制能力。

目前，M IMO雷达发射方向图设计是一个热门的研究课题［716］-。文献［7］提出了利用发射信号互相关矩阵设计发射方向图的思路。文献［8-12］基于待设计发射方向图与期望方向图匹配模型，迭代求解出发射信号相关矩阵，但未考虑旁瓣杂波抑制问题。文献［13-16］采用主瓣保形、最小化积分旁瓣和最小化峰值旁瓣准则，建立发射方向图匹配的凸优化模型，利用凸优化工具包［17］进行求解发射信号相关矩阵，然而这些优化准则都是基于杂波在空域均匀分布或近似均匀分布的前提，但在实际中，杂波在空域中大多非均匀分布。文献［18］针对非均匀杂波背景下的旁瓣杂波抑制问题，提出一种基于先验信息的M IMO雷达发射方向图设计方法，该方法以最大化回波信号中的信杂比为优化准则，优化设计发射方向图，但它不一定能保证接收信号经过滤波器输出后信杂噪比最大，此外，文献［18］主要针对地基平台。但在机载平台上，杂波具有空时2维（方位维和多普勒维）特性［1］，即杂波方位和多普勒成依赖关系，此时，文献［18］的信号模型不再适用。然而，利用杂波和目标的空时2维先验信息优化雷达发射方向图有可能显著降低旁瓣杂波能量，提高输出信号信杂噪比。因此，针对机载平台非均匀杂波背景下的旁瓣杂波抑制问题，本文提出一种基于杂波和目标空时2维先验信息及基于知识（Know ledge-Based， KB）的机载雷达发射方向图设计方法。该方法根据当前的杂波环境，在发射端设计中，利用了上一次相干处理间隔（Coherent Processing Interval， CPI）内杂波和目标的先验空时2维回波数据，以最大化空时匹配滤波输出信杂噪比为准则建立关于发射信号相关矩阵的优化代价函数设计机载M IMO雷达发射方向图，并采用半正定规划方法进行求解，实现旁瓣杂波抑制，提高输出信号的信杂噪比。

2 M IMO雷达信号模型

图1为机载雷达天线阵列的几何布局。为不失一般性，假设雷达平台以速度v沿X轴方向运动。0θ为方位角且Y轴为零方位角，φ为俯仰角，α为偏航角即雷达平台运动方向与雷达天线阵列的夹角，对于正侧视阵，偏航角α=0°，对于前视阵，偏航角α=90°。

图1 机载雷达几何示意图

假设一收发共置的机载M IMO雷达系统为正侧视阵列，即偏航角为α=0°，它由包含N个天线的均匀线阵（Uniform ly Linear Array， ULA）构成，阵元间距为d，各天线发射窄带的相位编码信号，发射信号的码长为L。令 xnl表示第n个天线在第l个时刻发射的基带信号，那么发射波形矩阵可以表示为

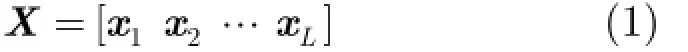
发射波形 sl的相关矩阵R可表示为

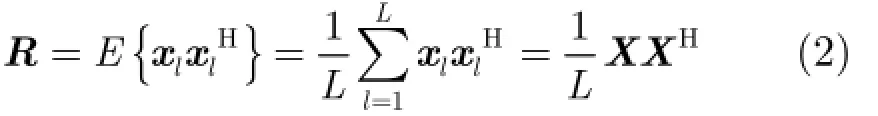
在远场方位角θs，俯角φ处合成的信号为

其中

为发射导向矢量。

现在以Δθ为间隔把整个空域离散成K个角度，即将空域划分为θ=［θ1θ2…θK］，忽略杂波脉内多普勒相移影响，则杂波统计特征在空域上相互独立，时域上对于同一发射信号相干且平稳。若不考虑误差等非理想因素，则假设β=［β1β2…βK］表示对应于K个离散角度的杂波强度。那么远场所有方向杂波的回波整理成矩阵可表示为

考虑单目标情况，假设目标在方位角θt，其后向散射系数为βt，目标的回波表示为

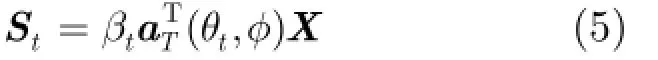
假设载机速度为v，机载雷达在一个相干处理间隔内，发射M个脉冲，基于窄带信号的假设，第m次脉冲第n个接收阵元接收到的杂波回波信号可表示为

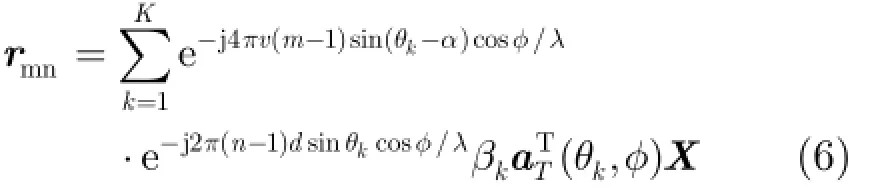
式（6）中4πv（m-1）sin（θk-α）cosφ/λ表示方位角θk处杂波回波信号第m次脉冲的相位延迟，2π（n-1） d sinθkcosφ/λ表示方位角θk处杂波回波信号第n个接收阵元的相位延迟。从式（6）可看出 rmn包含了所有方向的杂波回波信号。

若将M个脉冲N个接收阵元接收到的杂波回波信号r11， r12，…， rMN排成一个矩阵，则它为M× N ×L的3维矩阵，为了方便处理，本文利用⊗（kronecker乘积）将该矩阵转换成一个维数是MN ×L的2维矩阵 rc，那么 rc可表示为

其中

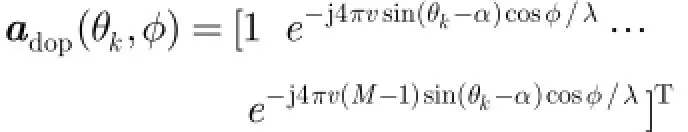
为慢时间导向矢量，

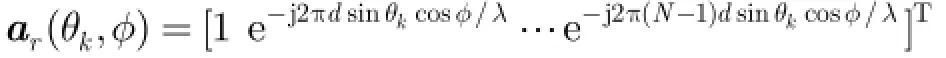
为接收导向矢量。

同理，接收到的目标信号 rt维数为MN× L，它可表示为

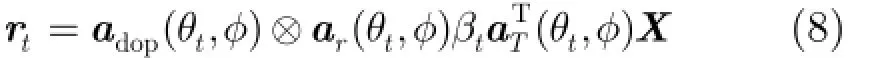
考虑噪声影响，此时接收到的回波可以近似地看作杂波、目标回波及噪声之和，即

其中 rn为噪声信号。

3 最优发射信号相关矩阵设计

接收机接收到的信号通常包含目标、杂波和噪声，它需要经过空时匹配滤波器才能用于检测跟踪，雷达对目标的检测跟踪性能与空时匹配滤波输出信号的信杂噪比密切相关。本文希望在不损失目标功率的条件下，分别利用了杂波和目标的空域信息和多普勒信息，有效地抑制杂波功率。因此，本文基于最大化空时匹配滤波输出信杂噪比准则对发射信号相关矩阵进行优化设计，可以从空时2维的角度实现杂波抑制，提高信杂噪比。

空时匹配滤波分为很多种，本文针对最大化空时匹配滤波输出信杂噪比这一准则，主要采用了如下设计思路。首先，接收信号经过接收波束形成器，在目标方位角产生高的增益，此时，主瓣能量大大地提高，旁瓣能量显著降低，旁瓣杂波得到抑制。接着，经过多普勒滤波器，利用主瓣杂波和目标的多普勒差异，实现主瓣杂波和目标的分离从而抑制主瓣杂波。空时匹配滤波器组由多普勒滤波器组和接收波束形成器构成，设计空时匹配滤波器组为

表示第m个多普勒滤波器的系数，ar（θt，φ）表示指向目标的接收波束形成器，假设目标在第m个多普勒通道。目标回波信号空时匹配滤波器的输出可表示为

杂波和噪声信号经过空时匹配滤波器在目标所在通道的输出可表示为

则根据式（11）和式（12）可以推导出输出信杂噪比为

其中Rt=E （ ZtZtH）表示目标空时匹配滤波器输出的相关矩阵，Rcn=E（ ZcnZcHn）表示杂波和噪声空时匹配滤波器输出的相关矩阵，Pt和tr（Rt）表示信号的输出功率， Pcn和tr（Rcn）表示杂波和噪声的输出功率。由于杂波和噪声不相关，将式（7），式（8），式（10），式（11），式（12）代入式（13）得

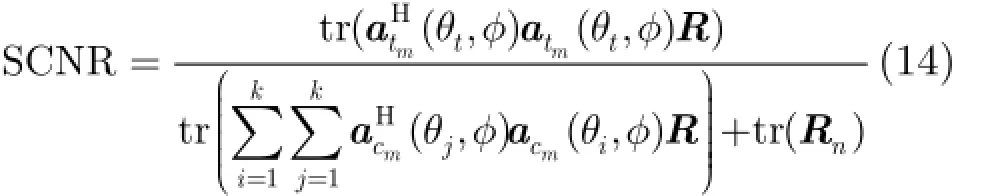
其中tr（Rn）为噪声输出功率。由于各个杂波块在空域相互独立，因此，式（14）可以简写为

其中

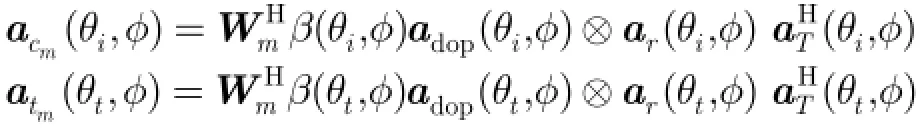
假设杂噪比为ρcn，式（15）变为

结合式（16）并对发射信号相关矩阵R引入约束，优化模型可描述为

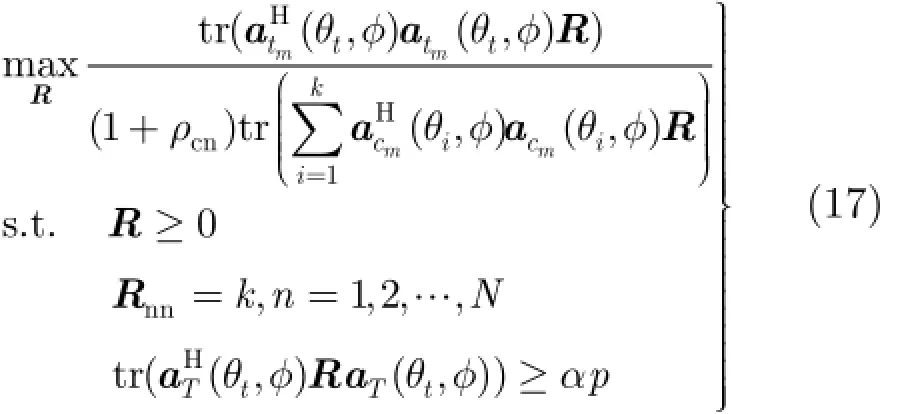
对于式（17），本文通过引入辅助变量t，将其转换为

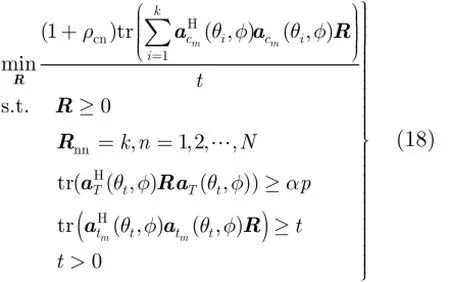
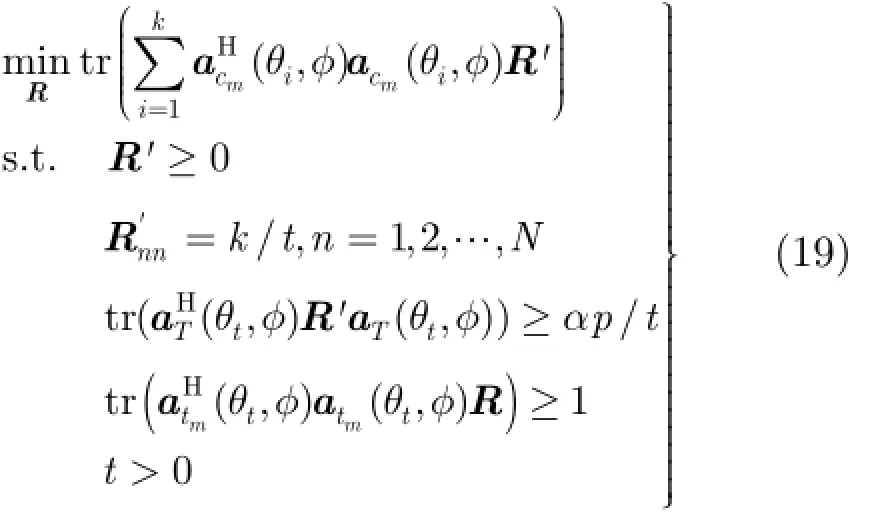
4 仿真实验

本节在正侧视阵列的情况下，为了说明本算法的实际应用价值，本文基于实测杂波数据做了仿真实验。为了说明提出的发射方向图设计方法的性能优势，将本算法与文献［18］的方法、最大化信噪比准则（传统发射）的优化结果做了对比。并进行了详细的分析。

假设雷达系统包含N=16个收发共置的阵元，阵元间距为半波长，单个CPI内发射脉冲数M= 10，脉冲重复频率PRF= 5000 Hz 。载机平台高度为H=5000 m ，平台速度为v=250 m/s。仿真实验中主要考虑目标所在距离单元的杂波，感兴趣目标在方位角θt=0°处，目标速度以vt=150 m/s 的径向速度远离雷达平台，目标幅度为10。

实测杂波幅度沿方位维的分布特性如图2所示。基于场景图2由式（17）优化得到的发射方向图如图3所示，基于最大化接收阵列信号信杂噪比准则优化得到的发射方向图如图4所示。图5是基于最大信噪比准则设计的发射方向图。由图3，图4和图5的优化结果可以看出，它们都在方位角θt=0°处产生了峰值，使得主瓣具有足够的发射功率，能够保证在接收端目标信号的回波有足够的功率。图3与图4均可以在强杂波区域产生了凹口，而且图3比图4有更深的凹口，更加有效地抑制了强杂波，而图5并没有抑制强杂波的能力。图6（a）和图6（b）分别是最大信噪比优化发射方向图和最大空时滤波输出信杂噪比优化发射方向图经过空时2维匹配滤波器输出的杂波功率谱，两图是在同一尺度下进行功率对比。两图中坐标（0，0）处为主瓣强杂波，坐标（-42，0.2889）处为方位维强杂波。从图6中可看出图6（b）优化发射方向图下的强杂波输出功率低于图6（a）（未优化）25.78 dB，降低了杂波功率，达到了抑制杂波的效果。此外，图6（a）和图6（b）中主瓣杂波功率未发生明显变化，这是因为优化方向图主瓣功率增益未发生明显衰减。表1为3种优化准则下设计的发射方向图接收信号经过空时匹配滤波器后的输出信杂噪比。从表1中可以看出，最大化空时匹配滤波输出信杂噪比准则和文献［18］的方法两种优化准则得到的信杂噪比分别优于最大化信噪比准则4.1378 dB和2.6187 dB。而最大化空时匹配滤波输出信杂噪比准则优于文献［18］的方法1.5191 dB。

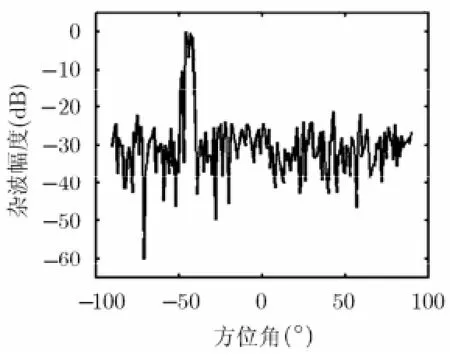
图2 方位维杂波的幅度

图3 最大化空时滤波输出信杂噪比准则优化发射方向图

图4 文献［18］方法的优化发射方向图

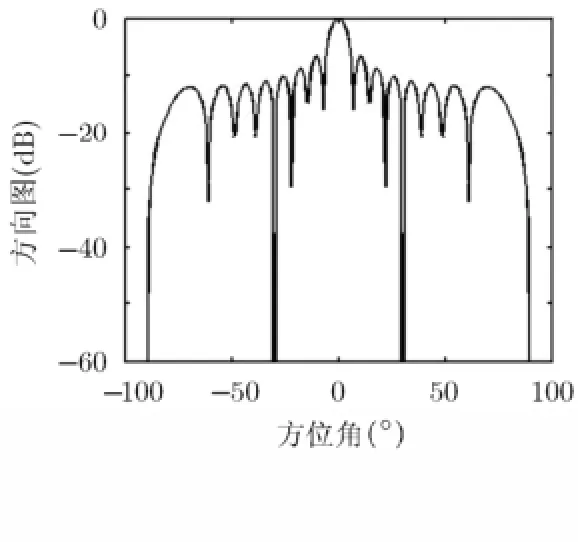
图5 最大化信噪比准则发射方向图

图6 最大化信噪比准则优化发射方向图和最大化空时滤波输出信杂噪比准则优化发射方向图空时2维滤波输出的杂波功率谱

表1 不同优化准则得到的输出信杂噪比（dB）

5 结束语

基于M IMO雷达波形分集的特性，结合杂波空时2维分布信息和目标的先验信息，本文提出了一种非均匀杂波背景下的机载M IMO雷达发射方向图设计方法，以最大化空时匹配滤波后输出信杂噪比为优化准则设计发射方向图，用以抑制旁瓣区域非均匀杂波能量来提高空时匹配滤波器输出信杂噪比。仿真实验表明，（1）本算法得到的方向图能够在目标方位角产生具有一定增益的主瓣，保证目标有足够的回波功率。（2）本算法得到的方向图能够在强杂波区域产生了凹口，抑制杂波功率。（3）接收到的回波信号经过空时匹配滤波后得到的输出信杂噪比较最大化接收阵列信杂噪比及最大信噪比的输出信杂噪比的结果得到了提升，为后续信号处理性能的提升提供了帮助。仿真实验也表明本文提出的方法是可行的。然而，本文算法主要用于机载雷达正侧视布阵的情况，对于非正侧视的发射方向图设计方法正在研究。此外，文中的优化准则只考虑了发射方向图的空域特性，对于波形的优化有待于进一步研究。

［1］ K lemm R. Princip les of Space-Time Adaptive Processing［M］. 3rd Edition， London: United Kingdom， the Institution of Engineering and Technology， 2006: 1-644.

［2］ 金林. 智能化认知雷达综述［J］. 现代雷达， 2013， 35（11）: 6-11. Jin Lin. Overview of cognitive radar w ith intelligence［J］. Modern Radar， 2013， 35（11）: 6-11.

［3］ Haykin S. Cognitive radar: a way of the future［J］. IEEE Signal Processing M agazine， 2006， 23（1）: 30-40.

［4］ Sun Y， He Z， and Li J. Cognitive space-time transm it pattern design［J］. International Journal of Antennas and Propagation，2014， http://dx.doi.org/10.1155/2014/141568.

［5］ Haimovich A M， Blum R S， and Cim ini L J. M IMO radar w ith w idely separated antennas［J］. IEEE Signal Processing M agazine， 2008， 25（1）: 116-129.

［6］ Li J and Stoica P. M IMO radar w ith colocated antennas［J］. IEEE Signal Processing M agazine， 2007， 24（5）: 106-114.

［7］ Fuhrmann D R and Antonio G S. Transm it beam forming for M IMO radar system s using signal cross-correlation［J］. IEEETransactions on Aerospace and Electronic Systems， 2008，44（1）: 171-186.

［8］ 胡亮兵， 刘宏伟， 杨晓超， 等. 集中式M IMO雷达发射方向图快速设计方法［J］. 电子与信息学报， 2010， 32（2）: 481-484. Hu Liang-bing， Liu Hong-wei， Yang Xiao-chao， et al.. Fast transm it beam pattern synthesis for M IMO radar w ith colocated antennas［J］. Journal of Electronics & Information Technology， 2010， 32（2）: 481-484.

［9］ Liu Y， Liu Z， Xie R， et al.. Transm it beam pattern synthesis and perform ance analysis for collocated M IMO radar［C］. 2013 International Conference on Radar， Adelaide， Australia，2013: 188-193.

［10］ Ahmed S， Thom pson J S， Petillot Y， et al.. Unconstrainted synthesis of covariance m atrix for M IMO radar transm it beam pattern［J］. IEEE Transactions on Signal Processing，2011， 59（8）: 3837-3849.

［11］ Ahmed S， Thom pson J S， Petillot Y， et al.. Finite alphabet constant-envelope waveform design for M IMO radar［J］. IEEE Transactions on Signal Processing， 2011， 59（11）: 5326-5337.［12］ Ahm ed S and A louini M S. M IMO radar transm it beam pattern design w ithou t synthesising the covariance m atrix［J］. IEEE Transactions on Signal Processing， 2014，62（9）: 2278-2289.

［13］ Gershman A B， Sidiropoulos N D， Shahbazpanahi S， et al.. Convex optim ization-based beam form ing［J］. IEEE Signal Processing M agazine， 2010， 27（3）: 62-75.

［14］ 罗涛， 关永峰， 刘宏伟， 等. 低旁瓣M IMO雷达发射方向图设计［J］. 电子与信息学报， 2013， 35（12）: 2815-2822. Luo Tao， Guan Yong-feng， Liu Hong-wei， et al.. Low sidelobe transm it pattern design for M IMO radar［J］. Journal of Electronics & Inform ation Technology， 2013， 35（12）: 2815-2822.

［15］ Gong P， Shao Z， Tu G， et al.. Transm it beam pattern design based on convex optim ization for M IMO radar system s［J］. Signal Processing， 2014， 94: 195-201.

［16］ Xu H， Wang J， Yuan J， et al.. M IMO radar transm it beam pattern synthesis via m in im izing sidelobe level［J］. Progress in Electrom agnetics Research B， 2013， 53（1）: 355-371.

［17］ G rant M and Boyd S. CVX: M atlab software for discip lined convex programm ing［OL］. http://stanford.edu/～boyd/cvx，2008.

［18］ 王旭， 纠博， 刘宏伟， 等. 一种基于先验信息的M IMO雷达发射方向图设计方法［J］. 电子与信息学报， 2013， 35（12）: 2802-2808. Wang Xu， Jiu Bo， Liu Hong-wei， et al.. A beam pattern design method for M IMO radar based on a p riori information［J］. Journal of Electronics & Information Technology， 2013，35（12）: 2802-2808.

施君南： 男，1988年生，博士生，研究方向为机载M IMO雷达认知发射.

纠 博： 男，1982年生，博士，副教授，研究方向为自适应信号处理、雷达自动目标识别、认知雷达.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达自动目标识别、认知雷达、协同探测.

A Beam pattern Design M ethod for A irborne M IMO Radar Based on Prior Information

Shi Jun-nan Jiu Bo Liu Hong-wei Wang Xu
（National Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071， China）

A beam pattern design method for the airborne Multiple Input Multiple Output （M IMO） radar based on the p rior information is p roposed to supp ress the sidelobe clutter in the non-homogeneous clutter environment. Using the two Dim ensional （2D） p rior in form ation of the target and clutter in the spatial and Dopp ler dom ain， the cost function for the correlation matrix of the transm ission waveform is established by em ploying the maximum output Signal-to-Clutter-plus-Noise Ratio （SCNR） criterion after the space-time matched filter and it can be solved by the Sem i-Definate Programm ing （SDP）. The simulation resu lts indicate that the transm ission beampattern optim ized by the p roposed method is able to increase effectively the SCNR output after the space-time 2D matched filter in the non-homogeneous clutter environment.

A irborne radar； M IMO radar； Signal-to-C lutter-p lus-Noise Ratio （SCNR）； Transm ission beam pattern；Space-time 2D matched filter

TN958

： A

：1009-5896（2015）05-1038-06

10.11999/JEIT140911

2014-07-11收到，2014-12-08改回

国家自然科学基金（61271291， 61201285），新世纪优秀人才支持计划（NCET-09-0630），全国优秀博士学位论文作者专项资金（FANEDD-201156），国家省部委基金和中央高校基本科研业务费专项资金资助课题

*通信作者：纠博 bojiu@mail.xidian.edu.cn