基于矩阵补全的天波雷达瞬态干扰抑制算法

李 茂何子述

（电子科技大学电子工程学院 成都 611731）

基于矩阵补全的天波雷达瞬态干扰抑制算法

李 茂*何子述

（电子科技大学电子工程学院 成都 611731）

瞬态干扰持续时间短、强度大，严重影响天波超视距雷达的性能。传统的瞬态干扰抑制方法需要预先抑制海杂波，且只能抑制强瞬态干扰，不能抑制弱瞬态干扰和噪声，该文提出一种基于矩阵补全的瞬态干扰抑制算法，该方法首先利用Teager-Kaiser算子进行瞬态干扰检测，然后将干扰数据剔除，最后利用海杂波和目标回波构成的Hankel矩阵的低秩性，通过改进的低秩矩阵补全算法进行数据恢复。该算法不仅能够抑制强瞬态干扰，而且能同时抑制弱瞬态干扰和噪声，提高了回波信号的信噪比。实测和仿真数据处理结果证明了算法的有效性。

天波超视距雷达；瞬态干扰抑制；矩阵补全；Teager-Kaiser算子

1 引言

天波超视距雷达可以探测超视距目标，探测距离范围一般为800～3800 km，因此主要用于远程预警。天波超视距雷达易受外部环境干扰。外部干扰会淹没目标信号，影响雷达性能，因此必须进行干扰抑制。天波超视距雷达的外部干扰可以分为3类：电离层杂波［1，2］、射频干扰［3］和瞬态干扰［49］-。射频干扰主要由高频辐射源引起；电离层杂波一般由雷达回波经电离层反射直接回到接收机形成；瞬态干扰持续时间较短，但是其能量较大，主要由雷电、流星余迹等引起［49］-。这3种干扰都具有一定方向性，所以可以通过自适应波束形成技术进行抑制，但是自适应波束干扰抑制技术需要一定数目的辅助天线；另外，对于瞬态干扰，由于其能量较强，可能出现干扰抑制不彻底的现象。为此，许多学者提出在慢时间域进行瞬态干扰抑制，即在匹配滤波和波束形成后，多普勒处理前，对各个距离采样单元数据分别进行瞬态干扰抑制。现有的瞬态干扰抑制算法主要分为两类：（1）先进行干扰位置检测，然后将干扰数据剔除，最后利用自回归（Auto-Regressive，AR）模型［4］、神经网络［5］或压缩感知［6］等插值方法进行插值，将数据恢复。文献［4］和文献［6］所提算法在检测干扰前，需要先进行杂波抑制，在进行杂波抑制时，很容易将瞬态干扰的部分能量也抑制掉，影响后续的干扰位置检测；（2）利用信号分解理论，将回波分解为多个分量，然后利用瞬态干扰持续时间短、能量强的特性，从多个分量中将瞬态干扰对应的分量剔除，然后用剩余分量信号合成回波信号［7-9］。文献［7］将回波信号分解为多个高斯基函数分量，文献［8］利用复经验模式分解方法将回波信号分解，这两种算法计算量较大，工程实现困难。文献［9］利用奇异值分解，将回波信号分解为多个正交信号，然后利用奇异值大小识别干扰信号，但是在实际使用时，很难确定奇异值门限值。

该文所提的算法其流程与第（1）类算法相同，但该文所提算法不需要预先对海杂波进行抑制，克服了第（1）类算法的缺点。在干扰数据检测和剔除后，利用海杂波和目标回波信号构成的Hankel矩阵具有低秩性的特点，使用改进的低秩矩阵补全算法进行缺损数据恢复。该文所提的算法具有两个优点：（1）在瞬态干扰能量较弱时，该文方法仍然能够抑制干扰；（2）算法在抑制干扰的同时，对噪声具有很好的抑制效果，提高了信噪比。

2 信号模型

天波超视距雷达某一距离-方位单元的回波信号可以表示为

其中m为脉冲数，M为相干积累脉冲数，s（m）= c（m）+ t（m）为海杂波和目标回波信号，c（m）为海杂波，t（ m）为目标回波信号，i（m）为瞬态干扰，n（ m）为加性高斯噪声，其方差为σ2。对于天波超视距雷达，海杂波的主要成份可以近似表示为两个Bragg峰信号［10］：

其中b为目标反射系数，q1= 4π v/ζ， q2= 4πβ/ζ，ζ为雷达波长。

3 干扰检测与数据恢复

3.1 干扰数据检测与剔除

其中xr（ m）和xi（ m）分别为x（m）的实部和虚部，Ψ（x（ m））= x2（ m）- x（m+1） x（m -1）。在文献［13］和

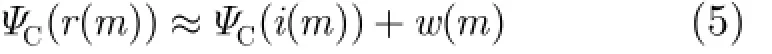
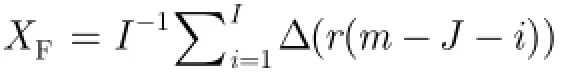
3.2 基于低秩矩阵补全的数据恢复

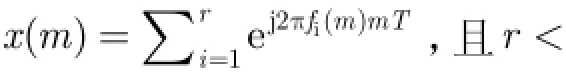
根据文献［10］中的结论，在海杂波展宽不严重，且目标机动性较弱的情况下，由s（m）构成的Hankel矩阵H（s）的秩近似为3。在天波雷达中脉冲积累数M一般远大于3，如M=256或512，因此，总能够构造一个Hankel矩阵H（s），使其满足rank（H（s））≪min（P，L）。令R=H（r）， S=H（s）， I=H（i）， N= H（n），这样式（1）中的回波信号可以表示为矩阵形式。

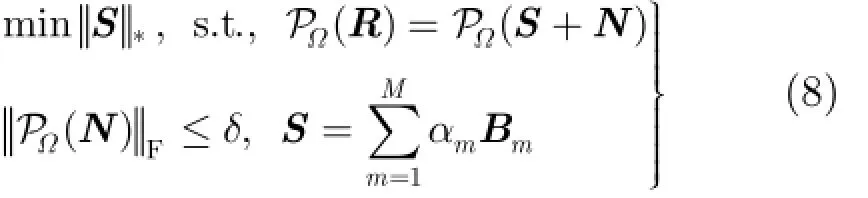
3.3 利用增广拉格朗日乘子法解优化问题

下面利用增广的拉格朗日乘子法［18］解式（8）中的优化问题。经典的矩阵补全算法只适用于实矩阵，该文中的矩阵为复矩阵，文献［19］提出将矩阵恢复算法直接分别用于复信号的实部和虚部，然后再合成复信号，这种处理方式的缺点是：实部和虚部单独处理时，没有利用复信号的相位信息。考虑到上述缺点，为了有效地利用相位信息，该文将经典矩阵补全算法直接扩展到复数域，复数域的拉格朗日函数可以表示为

步骤2 更新矩阵S

其中Ek=UΣVH表示矩阵Ek的奇异值分解。

其中Σij表示矩阵Σ的第ij个元素。

步骤3 更新矩阵Z

其中Ω=E-Ω，E为全1矩阵。

步骤4 更新矩阵N

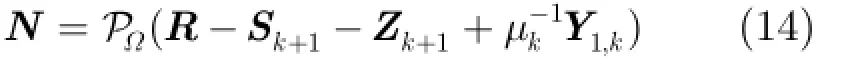
步骤5 更新向量α

其中αm，k表示向量α的第m个元素的第k次更新。

步骤6 更新Y1，Y2和μ

步骤7 如果式（17）不成立，算法未收敛，则令k=k+1转步骤2，否则转步骤8；

4 实测和仿真数据

在本节，对算法进行测试，验证算法的有效性。SO-CFAR参数设置如下：保护单元10J=个、参考单元8I=个、标称化因子10Λ=。

4.1 实测数据测试

本节利用实测数据验证算法的性能。为了验证算法的有效性，将该文方法与文献［7］中的时频方法及文献［6］中的压缩感知方法进行对比。文献［6］中的时频方法的基本思想是：将回波信号分解为多个高斯基函数，然后将基函数分量中同时具有短时宽和强能量特征的分量剔除掉，最后利用剩余的基函数分量重构信号，重构后的信号即为抑制干扰后的信号。文献［6］中的压缩感知方法先进行杂波抑制，然后进行干扰检测和干扰剔除，最后利用回波信号在频域的稀疏性，通过压缩感知方法进行数据重构。在处理实测数据时，发现使用文献［6］的杂波抑制方法，很难将杂波完全抑制，影响干扰位置检测，为公平比较，在压缩感知方法中，使用该文所提的Teager-Kaiser算子进行干扰位置检测。

图1给出了信号的幅度。图1（a）为原始信号的幅度，从图中可以看出，原始信号中存在两个瞬态干扰，即强干扰和弱干扰。在强干扰出现的位置，信号幅度突变明显。图1（b）显示了利用时频方法干扰抑制后信号的幅度，很明显强干扰几乎被完全抑制，时频方法对强干扰具有较好的抑制效果，但是对于弱干扰，时频方法基本没有抑制作用。图1（c）为经过压缩感知方法干扰抑制后信号的幅度，相比时频方法，压缩感知方法对弱干扰也具有一定的抑制效果，但是数据恢复后，强干扰处信号的幅度仍然存在起伏，这种起伏会引起信号频谱起伏，影响目标检测。图1（d）显示了利用本文方法干扰抑制后信号的幅度，通过与图1（a）对比，可以明显看到，本文所提的方法不仅能抑制强干扰，而且对弱干扰也有很好的抑制效果。

图2显示了Teager-Kaiser算子检测瞬态干扰的结果，从图中可以看出，在强干扰出现的位置，Teager-Kaiser算子的输出有较大的波动，这验证了Teager-Kaiser算子对瞬态干扰具有很好的敏感性，可以有效检测瞬态干扰。虽然在弱干扰处Teager-Kaiser算子输出也有波动，但是波动幅度并没有超过检测门限，Teager-Kaiser算子没有检测到弱干扰，然而图1（d）显示本文提出的算法能抑制弱干扰，这是因为，在利用矩阵补全算法进行数据恢复时，由于矩阵补全算法可以抑制噪声，而弱干扰能量较小，以至于它们的能量和噪声水平相当，弱干扰随噪声被一起抑制掉了。

图3给出了信号的多普勒谱。图3（a）为原始信号的多普勒谱，虽然可以从多普勒谱中发现目标，但是由于存在瞬态干扰，背景基底噪声起伏较大，几乎淹没了目标信号，如果直接进行目标检测，很难将目标检测出来。图3（b）为利用时频方法干扰抑制后信号的多普勒谱，与图3（a）相比，可以看出基底噪声明显降低。图3（c）为使用压缩感知方法抑制后信号的多普勒谱，图中基底噪声起伏较大，这种起伏由噪声和缺损信号重构误差引起。图3（d）显示了利用本文方法干扰抑制后信号的多普勒谱，与图3（b）和图3（c）相比，本文所提的方法有效地降低了噪声和干扰功率，提高了信噪比。

图1 信号的幅度

图2 Teager-Kaiser算子检测结果

为了体现弱干扰的影响，本文将原始信号中的弱干扰，添加到所提算法的处理结果中，构成合成信号，图4（a）中显示了合成信号的幅度，图4（b）给出了合成信号的频谱，与图3（d）对比可以看出合成信号的噪声基底，在整个频谱域出现了明显的起伏，影响后期的目标检测性。

文中提到的3种算法，都存在迭代过程，算法的计算量很大程度上依赖于迭代次数，很难根据计算复杂度比较3种算法的计算量，为此本文通过仿真程序的平均运行时间来近似对比3种算法的计算量。使用主频为3.1 GHz的双核计算机，进行512次实验，3种算法的平均运行时间分别为：58.7 s（时频方法）、17.4 s（压缩感知方法）和24.3 s（本文方法）。

4.2 仿真数据测试

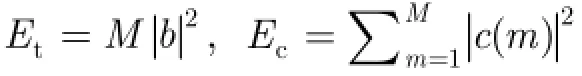
图5显示了信号的多普勒谱，其中SCR= -43.5 dB， CNR= 58.7 dB。图5（a）为原始信号的多普勒谱，从图中可以看出，背景基底噪声起伏较大，加速度目标信号完全被掩盖。为了对比本文算法的干扰抑制效果，图5（b）给出了无瞬态干扰和噪声情况下，海杂波和目标回波信号的多普勒谱，目标的径向加速度β=5 m/s2，目标信号的多普勒谱发生展宽。图5（c）为经过本文算法抑制瞬态干扰后，海杂波和目标回波信号的多普勒谱，从图中可以看出本文算法在抑制干扰的同时，降低了噪声功率，而且较好地恢复了海杂波和目标回波信号，这说明目标为弱机动目标时，本文所提算法仍然具有较好的干扰和噪声抑制效果。

图3 信号的多普勒谱

图4 合成信号

图5 仿真信号的多普勒谱

5 结束语

本文所提算法利用Teager-Kaiser算子对瞬态干扰进行检测，然后剔除干扰数据，然后，利用海杂波和目标回波信号构造的Hankel矩阵具有低秩性的特点，通过低秩矩阵补全算法对缺损信号进行恢复。本算法在干扰检测时，不需要预先抑制海杂波，且算法能够同时抑制强瞬态干扰、弱瞬态干扰和噪声。仿真数据和实测数据验证了算法的有效性，本算法实用性强，具有很好的工程应用前景。

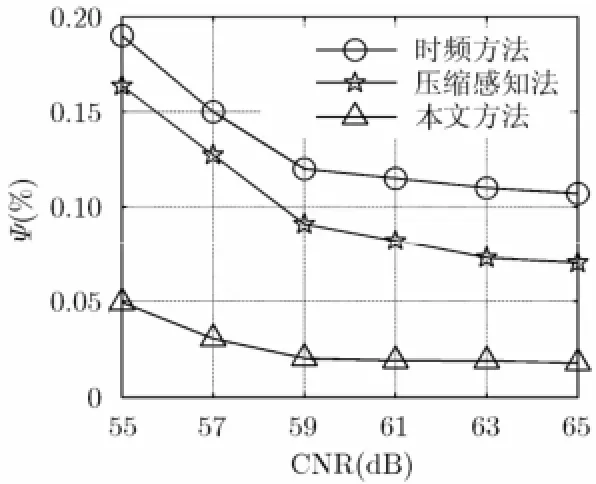
图6 性能对比图（SCR=- 37.3 dB ）

［1］ 熊新农， 万显荣， 柯亨玉， 等. 基于时频分析的高频地波雷达电离层杂波抑制［J］. 系统工程与电子技术， 2008， 30（8）: 1399-1402. Xiong Xin-nong， Wan Xian-rong， Ke Heng-yu， et al.. Ionospheric clutter supp ression in high frequency surface wave radar based on time-frequency analysis［J］. System s Engineering Electronics， 2008， 30（8）: 1399-1402.

［2］ T ian W en-long， Li Gao-peng， and Xu Rong-qing. Ionospheric clutter m itigation for high-frequency surface-wave radar using two-dimensional array and beam space processing［J］. IET Radar， Sonar & Navigation， 2012， 6（3）: 202-211.

［3］ Yi Jian-xin， Wan Xian-rong， Cheng Feng， et al.. Com putationally efficient RF interference suppression method w ith closed-form maximum likelihood estimator for HF surface wave over-the-horizon radars［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2013， 51（4）: 2361-2372.

［4］ 邢孟道， 保铮， 强勇. 天波超视距雷达瞬态干扰抑制［J］. 电子学报， 2002， 30（6）: 823-826.Xing Meng-dao， Bao Zheng， and Qiang Yong. Transient interference excision in OTHR［J］. Acta Electron ica Sinica，2002， 30（6）: 823-826.

［5］ 徐兴安， 吴雄斌， 陈骁锋， 等. 一种基于S变换的高频地波雷达瞬态干扰抑制方法［J］. 电子学报， 2014， 42（3）: 602-606. Xu Xing-an， Wu Xiong-bin， Chen Xiao-feng， et al.. An instantaneous interference supp ression app roach based on S transform s［J］. Acta Electron ica Sin ica， 2014， 42（3）: 602-606.

［6］ 全英汇， 张磊， 邢孟道， 等. 天波超视距雷达缺损信号的频谱重构［J］. 系统工程与电子技术， 2011， 33（8）: 1732-1737. Quan Ying-hui， Zhang Lei， Xing Meng-dao， et al.. Optimal reconstruction of spectrum w ith partial sam ples in OTHR［J］. System s Engineering and Electronics， 2011， 33（8）: 1732-1737.［7］ Guo X， Sun H， and Yeo T S. Transient interference excision in over-the-horizon radar using adaptive tim e-frequency analysis［J］. IEEE Transactions on Geoscience and Remote Sensing， 2005， 43（4）: 722-735.

［8］ 周忠根， 水鹏朗. 基于复数据经验模式分解的天波超视距雷达瞬态干扰抑制［J］. 电子与信息学报， 2011， 33（12）: 2831-2836. Zhou Zhong-gen and Shui Peng-lang. Transient interference suppression based on comp lex em pirical m ode decom position in over-the-horizon radar［J］. Journal of Electronics & Information Technology， 2011， 33（12）: 2831-2836.

［9］ 陈希信， 黄银河. 基于矩阵奇异值分解的高频雷达瞬态干扰抑制［J］. 电子与信息学报， 2005， 27（12）: 1879-1882. Chen Xi-xin and Huang Yin-he. A SVD-based approach of suppressing transient interference in High-Frequency radar［J］. Journal of E lectronics & Inform ation Technology， 2005，27（12）: 1879-1882.

［10］ Poon M W Y， Khan R H， and Le-Ngoc S. A singular value decom position （SVD） based method for suppressing ocean clutter in high frequency radar［J］. IEEE Transactions on Signal Processing， 1993， 41（3）: 1421-1425.

［11］ Yasotharan A and Thayaparan T. Tim e-frequency method for detecting an accelerating target in sea clutter［J］. IEEE Transactions on Aerospace and Electronic Systems， 2006，42（4）: 1289-1310.

［12］ Xu J， Xia X G， Peng S B， et al.. Radar maneuvering target m otion estim ation based on generalized Radon-Fou rier transform［J］. IEEE Transactions on Signal Processing， 2012，60（12）: 6190-6201.

［13］ Kandia V and Stylianou Y. Detection of sperm whale clicks based on the Teager-Kaiser energy operator［J］. Applied Acoustics， 2006， 67（12）: 1144-1163.

［14］ Kand ia V and Sty lianou Y. Detection of creak clicks of sperm whales in low SNR cond itions［C］. Proceedings of the IEEE Oceans， B rest， France， 2005: 1052-1057.

［15］ Richards M A. Fundamentals of Radar Signal Processing［M］. New York， USA， Tata M cGraw-Hill Education， 2005: 364-370.

［16］ Tanner J and W ei K. Normalized iterative hard th reshold ing for m atrix com p letion［J］. SIAM Journal on Scientific Com puting， 2013， 35（5）: S104-S125.

［17］ Liu G and Li P. Advancing matrix com pletion by modeling extra structures beyond low-rankness［OL］. http://arxiv. org/abs/1404.4646.

［18］ Peng Y， Ganesh A， W right J， et al.. RASL: robust alignm ent by sparse and low-rank decom position for linearly correlated images［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（11）: 2233-2246.

［19］ Yan H， W ang R， Li F， et al.. G round m oving target extraction in a multichannel w ide-area surveillance SAR/GMTI system via the relaxed PCP［J］. IEEE Geoscience and Rem ote Sensing Letters， 2013， 10（3）: 617-621.

［20］ Zhou X， Yang C， and Yu W. Moving ob ject detection by detecting contiguous outliers in the low-rank rep resentation［J］. IEEE Transactions on Pattern Analysis and M achine In telligence， 2013， 35（3）: 597-610.

李 茂： 男，1981年生，博士生，研究方向为天波超视距雷达信号处理、M IMO雷达信号处理.

何子述： 男，1962 年生，博士，教授，博士生导师，研究方向为天波超视距雷达技术、M IMO雷达信号处理 、宽带数字阵雷达技术.

Sky-wave Radar Transient Interference Supp ression Based on M atrix Com p letion

Li Mao He Zi-shu
（School of Electronic Engineering， University of Electronic Science and Technology of China， Chengdu 611731， China）

The transient interference can dramatically degrade the performance of over-the-horizon radar. The traditional interference supp ression methods need to supp ress the sea clutter， and only can supp ress the strong transient interference， not m itigate the weak one and the noise. A novel interference suppression m ethod is proposed based on the low-rank matrix com pletion. Firstly， the p roposed method detects the interference via the Teager-Kaiser operator， subsequently excises the interference data. Then， considering that the Hankel matrix of clutter-p lus-target signals is low-rank， the matrix comp letion method is exp loited to recover the interferenceremoved signal. The proposed algorithm can suppress not only the strong interference， but also the weak one and the noise， imp roving the signal to noise ratio of echo. The simu lation and experimental resu lts demonstrate the effectiveness of the proposed method.

Over-the-horizon radar； Transient interference supp ression； Matrix comp letion； Teager-Kaiser operator

TN958.93

： A

：1009-5896（2015）05-1031-07

10.11999/JEIT140973

2014-07-23收到，2015-01-12改回

国家自然科学基金重点项目（61032010）资助课题*通信作者：李茂 limao164@163.com