粗糙集在项目认知属性标定中的应用*
2015-02-05唐小娟丁树良俞宗火
唐小娟丁树良俞宗火
(1南昌航空大学数学与信息科学学院,南昌330063)(2江西师范大学计算机工程学院,南昌330022)(3江西省心理与认知科学重点实验室,南昌330022)(4江西师范大学心理学院,南昌330022)
1 引言
当代社会已经迈入知识经济时代,为了确保学生未来能更好地适应以知识为基础的工作环境,保持竞争力,同时为了教师能够更多地了解和掌握学生在认知上的优点和弱点,教学评估工作需不断地更新和完善。但在标准测量理论(Standard Test Theory)中,所测心理特质被当作纯统计量来考虑,无法体现被试具体的知识结构和心理特质的实质内容(Anastasi&Urbina,1997)。正是在这一背景下,认知诊断测验顺势崛起,已然成为新一代测验理论(Test Theory for a New Generation of Tests)的核心(Frederiksen,Mislevy,&Bejar,1993)。
在认知诊断中,刻画项目最重要的特征是认知属性。分析和标定测验项目的认知属性是认知诊断中最为基础的工作。以往对认知属性的标定主要依赖专家的主观判断,陈平和辛涛(2011)、汪文义、丁树良和游晓锋(2011)提出采用认知诊断计算机化自适应测验(Cognitive Diagnostic Computer Adaptive Testing,CD-CAT)这一概率统计方法对新增项的认知属性进行估计,Liu,Xu和Ying(2012,2013)采用统计方法进行估计和标定。专家提出的这些标定方法存在耗时、费力、成本高等问题,CD-CAT辅助项目认知属性的标定,无论是理论上还是实践上,对以往完全依靠人力标定认知属性都是一个重要的突破。但计算机化自适应测验(Computer Adaptive Testing,CAT)有其自身的局限,CAT的这些局限必然会影响其子类CD-CAT的应用:如,CAT的题库建设费用昂贵,甚至每个项目大约花费1000美元左右(Chang,2014);周期长;而且根据美国的No Child Left Behind(NCLB)法案,在美国计算机自适应测验被禁止使用于学生的阅读、数学和科学等学科的成就评估之中(Quellmalz&Pellegrino,2009,p.76)。认知诊断在形成性评估中非常有用,因此,课堂测验(Classroom assessment)被认为是认知诊断的最佳应用场所(Gierl&Leighton,2007)。但真正将认知诊断应用于课堂会遇到如下问题:第一,认知诊断目前主要应用于一些大型的考试之中,反馈不及时,无法真正起到辅助教学的作用(Huff&Goodman,2007;Leighton&Gierl,2007),限制了认知诊断的应用;第二,在未知项目参数的情况下,原有的基于概率统计的认知诊断模型对被试和项目的容量有较高的要求,因此,要将认知诊断灵活地运用于课堂教学中去,已有的认知诊断模型存在很大局限。这就需要寻求一种新的、适合于小规模课堂教学的项目认知属性的辅助标定方法。这对于拓广认知诊断的应用范围,使认知诊断真正起到诊断学生认知结构、辅助教学的作用,至关重要。本研究采用粗糙集(Rough Set)理论导出的方法对项目认知属性进行标定,该方法无需已知项目参数,故对被试量无太高要求,正好适合于课堂评估。
1.1 认知属性与认知诊断
认知属性(Cognitive Attribute)指知识和认知加工技能(Tatsuoka,2009,p.7)。一个测验项目可以具有多个认知属性,同一认知属性也可出现在多个测验项目之中。比如,阅读测验题需要具备认识字词或由上下文推敲不认识的字词的能力,并会涉及到记住细节的能力、将事实与意见区分开的能力、根据上下文线索进行猜测的能力等等(McGlohen,2004)。认知属性是认知诊断区别于经典测量理论(Classical Test Theory,CTT)和项目反应理论(Item Response Theory,IRT)等标准测量理论的最重要特征。CTT在编制测验项目时,采用总分指标评价被试能力,将个体在总体中的相对位置进行排序;IRT虽然考虑了被试在测验项目上的作答反应与能力间的关系,但能力指标只是一个统计含义上的概念,并没有真正揭示其内在心理含义。在CTT和IRT等标准测验理论中没有合适的算法将同一项目中含有的多个认知属性分开,因此只能假定一个项目只测量一个认知属性,但这在实际中可能不成立。正因为如此,这些心理测量理论与方法不能指出被试具体掌握了哪些内容,没有掌握哪些内容,更无法诊断被试错误作答的原因。构念效度(American Psychological Association,American Educational Research Association,&National Councilon Measurements Used in Education,1954)的提出代表了心理测量从功能主义向结构主义的转变(Cronbach&Meehl,1955),结构主义旗下的因素分析、聚类分析和传统的潜在类别模型虽然能够产生因素、族类或类别,在一定的程度上体现了对测验内容进行厘清的企图,但这些探索性方法只能将观察到的反应分成相似的类别或模式,却无法提供明确的解释(Tatsuoka,2009,p.xi)。正是因为有认知属性这一项目特征,心理测量学家将认知心理学中获得的心理模型和心理计量模型结合起来,建构认知诊断模型(Cognitive Diagnosis Model,CDM),通过认知诊断测验设计,将被试在项目上的作答与被试的知识、能力联系起来,对被试的认知结构和心理加工过程进行了解,即通过测验可以了解被试对知识点的掌握情况。
1.2 项目认知属性标定
要进行认知诊断,必须在命题前或测验后分析出测验项目测量的知识能力(特质)(Leighton,Gierl,&Hunka,2004),并对项目所测的认知属性进行标示,这一过程便是项目认知属性标定。在认知诊断中,认知属性是如此重要,对项目的刻画,可以不包含难度、区分度、猜测参数等心理计量学指标,却不可以没有认知属性。但项目认知属性标定是一件非常复杂而费劲的工作(DeCarlo,2011)。从现有的文献来看,主要有两种认知属性标定方法:一是完全由专家对项目进行分析并对项目认知属性进行标定;由于项目认知属性标定的复杂性,当认知属性较多或题量较大时,完全由专家来标定则工作量非常大且耗费成本较高,更重要的是,专家们经常对某些项目认知属性标定有分歧,很难达成一致意见。比如,多批专家对Tatsuoka(1990)分数减法认知诊断测验中的20个项目进行认知属性标定,20年过去了,尚有争议。二是在专家对一部分项目认知属性标定的基础上,采用认知诊断计算机化自适应测验的方法对其他项目的认知属性进行估计(陈平,辛涛,2011;汪文义等,2011),或采用传统统计方法进行标定(Liu et al.,2012,2013)。前面已述及CAT和CD-CAT的前期建设的耗费成本高,且要求被试样本量大,测验项目多等限制,故难于解决用于随堂测验的项目认知属性标定问题。下面我们介绍粗糙集方法以解决这一问题。
2 采用粗糙集进行属性自动标定方法
粗糙集(Rough Set)是由波兰学者Pawlak Z.提出的处理模糊和不确定性知识的数学工具,其主要思想就是在保持分类能力不变的前提下,通过知识约简,导出问题的决策或分类规则(Pawlak,1991)。该方法无需额外信息,利用已知的信息或知识去近似刻画不精确或不确定的概念,或者依据观察、度量的结果去处理不确定的现象和问题(张文修,吴伟志,梁吉业,李德玉,2001)。
粗糙集的分类机制使它有应用于心理测量的可能:心理测量的本质是用定量方法对被试的心理特质进行描述,并将不同的被试区分开来(余嘉元,2008)。从这一点来讲,粗糙集和心理测量在本质上有共同之处。一些学者已将粗糙集应用于心理测量(郭昭麟,2009;刘丽铃,2010;余嘉元,2008),并取得了一定的效果。如:郭昭麟和刘丽铃采用粗糙集中属性约简方法对试题进行删减,从而选取较好的试题测量被试;余嘉元采用属性约简方法对人事干部胜任力评估数据进行分析。这些研究在一定程度上佐证了粗糙集应用于心理测量的可行性,但这些粗糙集的运用还没有涉及认知诊断。认知诊断是模式识别(Tatsuoka,1995,2009),也可以说是诊断分类,而粗糙集在模式识别与分类方面有较为成功的应用(史忠植,2002,p.143)。Tang和Ding(2012)对粗糙集应用于认知诊断分类进行尝试,但这只是初步的研究,仅仅表明粗糙集可以用于认知诊断分类,没有进行更加深入的探讨。本文欲使用粗糙集对认知诊断中的认知属性标定问题进一步探讨。
2.1 粗糙集的基本要素
认知诊断是根据项目所涉及的认知属性和被试作答反应两方面的信息对被试进行分类。在粗糙集语境下,对被试的分类在决策表中进行,决策表表示当满足某些条件(具备哪些知识属性)时,决策(行为、操作、控制及分类等)应当如何进行。因此,首先需要建构决策表,并对决策表中的属性进行约简,然后提取决策规则,最后根据提取的规则将研究对象进行分类。从这个意义上来说,决策表、属性约简和决策规则是粗糙集中三个非常重要的因素。
2.1.1 决策表
设U是由研究对象组成的有限集合,称为论域。任何子集X⊆U称为U中的一个概念或范畴。U中的任何概念族称关于U的抽象知识,简称知识。粗糙集主要是对在U上能形成划分的那些知识感兴趣。集合U的一个划分确定U的元素间的一个等价关系,即一种知识,U上的一族划分也就确定一族等价关系,称为关于U的一个知识库(Knowledge Base)。知识库中包含大量(实例)的信息,通常是许多实例的原始记录。
决策表定义为具有条件属性和决策属性的知识表达系统(张文修等人,2001),是一类特殊而重要的知识表达系统。在数学上,知识表达系统可用S=(U,A,V,f)的形式来表达,通常也用二维信息表S=(U,A)来代替,其中的数据以等价关系表的形式表示。决策表的行对应研究对象(实体),所有研究对象的集合称为论域U。在认知诊断中,为了研究被试对属性的掌握情况,可设U为所有被试类型,即U为被试的知识状态(Knowledge States,KS)集合。列对应研究对象的属性(这里的属性并非是认知诊断中的认知属性),一个属性对应一个等价关系,即一种知识,所有属性构成一族等价关系,即多种知识,因此决策表可以看作是知识库。所有属性构成属性集A(即一族等价关系),A可以分为条件属性集C和决策属性集D,即A=(C,D)。如果视一个项目为一个属性(即一种知识),所有研究对象在该项目上作答与在别的项目上的作答可能不同,可视为一种划分,划分结果将研究对象分为作答正确和作答错误两类,因此,所有项目组成条件属性集C自然对应认知诊断测验蓝图,即测验Q矩阵,记为Qt,Qt每一列表示一个项目,即条件属性中的一个属性;而决策属性集D可对应认知诊断中的知识状态的集合,即Qs,被试的知识状态是一个等价关系,被试集合当然可以按知识状态进行划分;所以,A=(C,D)=(Qt,Qs)。值得注意的是:认知诊断中的认知属性和粗糙集中的属性是从不同角度对属性进行定义,前者是从认知心理学中认知加工过程的角度定义,后者是从数学的等价关系角度定义。两种之间是有区别的,但是有些认知属性若具备等价关系的特性,则也可视为粗糙集中属性。对象的信息是通过指定对象的各属性值来表达,S中的V表示对研究对象的属性赋值的集合,在认知诊断中每一类被试V的值为这类被试类型对各个项目(即条件属性)的期望作答形成理想反应模式(Ideal Response Pattern,IRP)和该类被试具体的知识状态(决策属性);f:A→V是从A到V的映射,即对应规则,是对每个研究对象的每个属性具体赋值。
2.1.2 属性约简
实际工作中,如果用原始实例记录构建知识库,由于在研究对象知识的选取上带有一定的主观性,所以各知识在知识库中显然不是同等重要的,还可能有一些是冗余的,在保证信息表分类能力不变的条件下,去除其中那些不重要的和冗余的知识,必须进行知识约简(Knowledge Reduction),而属性即知识,则知识约简也即属性约简。由上所述,在认知诊断中,若项目被设定为条件属性,则属性约简实际上是把对分类无用的项目进行删减(见2.3(2)),以提取更加简单的决策规则。在本研究中欲采取穷举算法对属性进行约简。决策表的约简是对知识库的一种提炼,从决策表的条件属性集合去掉那些对决策属性不重要的属性,约简仅仅是从属性(知识)的层面上对决策表进行简化。而要使知识具体化,最重要是从决策表中提取决策规则。
2.1.3 决策规则
在属性约简的基础之上,进一步提炼决策规则,从简化后的决策表中提取的每一个蕴涵式φ→ψ称为一个决策规则,φ、ψ分别称为决策规则的前件和后件,决策规则的前件φ实际上是决策表所能判断对象集合的全体,即决策表具有的识别能力,决策规则的后件ψ是根据决策表的识别能力(范围)所能得出的结论。每条决策规则表示当满足某些条件时,将得到怎样的决策结果。
2.2 粗糙集应用于认知诊断的原理
由前所述,认知诊断分类是一种模式识别。模式识别分为特征提取和分类两部分。粗糙集主要思想是在保持分类能力不变前提下,通过知识约简,导出问题的决策或分类规则,然后用规则进行分类。其中导出分类规则是特征提取部分,而使用规则分类则是分类部分。以估计被试的知识状态为例,具体如下:
(1)特征提取部分:建构用于导出分类规则的决策表,决策表与认知诊断各部分对应如图1。其中,U为研究对象,即被试知识状态类型,以具体自然数编号区分;Qt为测验Q阵,一列代表一个施测项目,对应于条件属性C中的一个属性(列),条件属性设置的个数等于施测项目的个数,决策属性D为学生Q阵(Qs),对应被试类型U的具体知识状态;决策表中的一行代表一类被试在所有施测项目上的理想反应模式和这类被试的知识状态,表示产生该作答模式的被试具有的知识状态;所有C和D上的赋值,即每类被试在所有项目上的作答和知识状态构成了集合V,由A到V构成一个映射f:A→V。决策表按上述要求建立后,则先约简再提取决策规则,也即特征提取。
(2)分类部分:在分类表中,U为所有待估被试,C与决策表的C一致,分类表中最后一列为估计出的知识状态,也就是说,表中每一行由三部分组成,第一部分为第一列,即待估被试编号,第二部分为中间的一些列,表示被试在所有施测项目上的作答结果,即被试的观察反应模式(Observed Response Pattern,ORP),第三部分为最后一列,即估计出的知识状态,如表1。
根据上面提取的规则和被试的观察反应模式,将被试进行分类。

图1 用于认知诊断的决策表及各部分对应情况

表1 用于认知诊断的分类表
从图1和表1中可以看出,特征提取部分对应认知诊断中的Qs、理想反应模式和Qt,分类部分对应认知诊断中的Qt、ORP和估计的KS。
2.3 粗糙集进行项目认知属性标定的基本步骤
对项目认知属性进行标定的基本原理是在属性之间不存在补偿作用条件下,由被试的知识状和施测项目,根据理想反应计算的规则,通常只有掌握项目所有认知属性的被试才能对项目正确反应,而被试在测验上的观察反应模式可以看成是带有误差的理想反应模式,由此可以由观察反应模式大致推算项目中认知属性向量。这有点像项目反应理论中项目难度标定(游晓锋,丁树良,刘红云,2010),当然项目认知属性向量是多维,可以想象,标定项目认知属性向量的难度更大。项目认知属性的自动标定步骤为:
第一步:估计被试的知识状态;
第二步:由第一步估计被试的知识状态和所有项目类型,构建项目认知属性自动标定决策表,并提取决策规则;
第三步:由第二步提取的决策规则自动标定项目认知属性。
下面以5个认知属性的收敛型结构为例,以说明项目认知属性自动标定方法:
第一步估计被试的知识状态
欲估计被试知识状态,首先需已知所有可能的项目类型和所有被试知识状态类型两方面的内容,通过被试在施测项目上的作答来确定被试属于哪种知识状态。已知认知属性个数和属性层级结构即可以获得相应的可达矩阵R;基于可达矩阵R,采用扩张算法(Ding,Luo,Cai,Lin,&Wang,2008;丁树良,祝玉芳,林海菁,蔡艳,2009;杨淑群,蔡声镇,丁树良,林海菁,丁秋林,2008)便可以得到项目类型与被试知识状态类型。如图2,具有5个属性的线型结构,所有项目类型为(1,0,0,0,0),(1,1,0,0,0),(1,1,1,0,0),(1,1,1,1,0),(1,1,1,1,1),在所有项目类型上加上被试知识状态全无情况,即(0,0,0,0,0),便得到所有被试知识状态,记为Qs:(0,0,0,0,0),(1,0,0,0,0),(1,1,0,0,0),(1,1,1,0,0),(1,1,1,1,0),(1,1,1,1,1);5个属性的收敛型结构,所有项目类型为:(1,0,0,0,0)、(1,1,0,0,0)、(1,1,1,0,0)、(1,1,0,1,0)、(1,1,1,1,1)、(1,1,1,1,0),同样得到Qs:(0,0,0,0,0),(1,0,0,0,0)、(1,1,0,0,0)、(1,1,1,0,0)、(1,1,0,1,0)、(1,1,1,1,1)、(1,1,1,1,0)。本例考察的是收敛型结构,从所有项目类型中随机选取1至5个项目作为施测项目,记为Qt,依次为:(1,0,0,0,0)、(1,0,0,0,0)、(1,1,0,0,0)、(1,1,1,0,0)、(1,1,0,1,0),这些项目用于估计被试的知识状态。
在具有被试类型、施测项目及被试观察反应模式的条件下,可按如下过程估计被试知识状态:

图2 5个属性的线型和收敛型属性层级结构
(1)构建决策表(见表2)
决策表由论域、条件属性和决策属性构成。论域中研究对象的个数由Qs的列数来确定,认知属性个数和结构不同,Qs则不同,如图2所示:5个属性的线型结构,Qs中含6个对象,收敛型结构为7个;如果考虑认知属性之间不存在先决关系,即认定为独立结构,则Qs有2=32列,即有32种对象类型。本例考虑收敛型结构,则Qs有7种类型,研究对象U的个数设为7,施测项目(Qt中的列)1至5设为条件属性1至5,决策属性设为Qs,如上所述,每一行表示相应被试的理想反应模式和产生该作答模式对应的知识状态,如第二行中第二类被试在条件属性1至5上的作答结果分别为1、1、0、0、0,其对应的知识状态为(1,0,0,0,0)(见表2)。

表2 5个属性收敛结构的决策表
(2)对表2,采用穷举算法对属性进行约简。
结果表明属性1和属性2(也即项目1和项目2)对分类所做出的贡献是一样的,从决策表也可以直观看出所有被试类型在项目1和项目2上的所答结果完全一致,对分类无差别,故可以删减一个属性。当然并不是所有的决策表都可以通过目测看出多余的属性,一般地,都要采用一定的算法进行删减。通过删减第2个属性(即第2个项目)可得新的决策表(表3)。

表3 属性约简后的决策表
从新的决策表(表3)提取决策规则。可以说,应用粗糙集进行认知诊断,实际上是一种基于规则的分类。约简和提取决策规则的整个过程在RSES(Rough Set Exploration System)软件中进行,该软件专门用于处理粗糙集中的问题。事实上,决策表可以看作一个无参数的认知诊断模型,由表1可以看到,一旦认知属性结构已知,则可以构建决策表,表中无需包括项目参数在内的任何参数,而只需施测项目认知属性即可,因而由项目参数带来的认知诊断中任何问题均可避免,这是粗糙集做认知诊断的优势之一。
通过属性约简,总共提取了8条决策规则:规则一:(atribute1=0)=>(knowledgestates=00000)规则二:(atribute2=0)=>(knowledgestates=00000)规则三:(atribute1=1)&(atribute3=0)=>(knowledgestates=10000)
规则四:(atribute2=1)&(atribute3=0)=>(knowledgestates=10000)
规则五:(atribute3=1)&(atribute4=0)&(atribute5=0)=>(knowledgestates=11000)
规则六:(atribute4=1)&(atribute5=0)=>(knowledgestates=11100)
规则七:(atribute4=0)&(atribute5=1)=>(knowledgestates=11010)
规则八:(atribute4=1)&(atribute5=1)=>(knowledgestates={11111,11110})
在属性约简的过程中,因为项目1与项目2相同,所以删除其中一个项目,表3表示删除了项目2,所以由表2提取的八条规则中,其中规则一与规则二作用相同,规则三和规则四作用一样,因此规则二与规则四可以剔除,也即实际上是六条决策规则。决策规则一表示如果第一个属性(即项目1)上的作答为“0”,则被试的知识状态为(0,0,0,0,0),决策规则八表示第四和五个属性(即项目4和5)上作答结果均为“1”,则被试知识状态可能为(1,1,1,1,1)或(1,1,1,1,0),可能性各为50%,其他规则类似说明。以上规则依据认知属性结构依次有序地对认知属性进行考察,因为认知属性间存在着先后或并列关系,因而六条决策规则一、三、五、六、七、八存在优先级差异,如图2的5个属性收敛型结构,先考察第一个认知属性,对应规则一、三;再考察第二个认知属性,对应规则五;然后考察第三或第四个认知属性,对应规则六和七;最后考察第五个认知属性,对应规则八。其优先级依次递降(若观察反应模式同时满足规则一和五时,则优先考虑规则一,也即优先考虑第一个认知属性,判知识状态为(0,0,0,0,0))或呈并列关系(如规则六和七,考察第三和第四个认知属性)。
(3)由决策规则将被试进行分类
该过程同样在RSES中进行。
举例说明如何利用决策规则进行分类的方法:由被试的观察反应模式(见表4),被试1在第一个项目上的作答为“0”,由决策规则一知,被试的知识状态为(0,0,0,0,0);被试2在第一个项目上的作答为“1”,第三个项目上的作答为“0”,由决策规则三知,被试的知识状态为(1,0,0,0,0);被试6和7在项目4和5上的作答均为“1”,说明他们的知识状态有两种可能,且可能性均为50%,RSES分析两被试知识状态均判为(1,1,1,1,1),其他依次类推。
表4是由RSES软件分类的结果,从该表可以看到,七个被试中,只有第七个被试在第五个认知属性上的估计有误,采用类似知识状态模式判准率与属性边际判准率公式,可得模式标定准确率为85.71%,属性边际标定准确率为97.14%。

表4 利用决策规则将被试进行分类
特别值得一提的是:在整个估计过程中,被试估计对被试数量和项目参数(如猜测参数等)是否已知无太多要求,体现出采用粗糙集对被试进行分类的优势;提取的规则中,出现了规则八指向两个知识状态的情况,而这种情况可能是由Qt设计不合理或约简算法不佳造成的。事实上,就像其他认知诊断模型一样,如果测验蓝图设置不合理,无论属性个数和项目数多少,属性关系是否复杂,在分类过程中都会出现如下的混乱的情形:好几个知识状态对应同一个理想反应模式,或者说同一个理想反应模式可能对应若干个知识状态。而被试的观察反应模式可以看成是带有随机误差的理想反应模式,因此这时候极有可能会出现被试指向几种知识状态的情况,这也是为什么现在认知诊断不能百分百精确诊断的原因之一,而不仅仅是在粗糙集中会出现这种情况。因此,要改变这种情况可考虑重新设计Qt或采用其他更适合的约简方法,根据被试作答,尽量把被试指向一种知识状态,以进一步提高分类准确率。从给定的项目4((1,1,1,0,0))和项目5((1,1,0,1,0))来看,这两个项目实际上没有涉及到第五个认知属性,事实上,因为随机选题,估计被试采用的所有项目都没有涉及到第五个认知属性,所以难以分辨被试是否拥有它,因此,测验蓝图的设计是非常重要的。一旦出现这种情况,软件会随机指派该规则中某种知识状态给被试。
第二步由第一步估计被试的知识状态和所有项目类型构建项目认知属性自动标定决策表。事实上,估计被试知识状态与估计项目认知属性是一个对偶过程,故在建构估计项目认知属性的决策表中,把由第一步估计被试的知识状态作为条件属性,收敛型结构将由扩张算法获得的所有项目类型的认知属性向量为决策属性,计算估计的被试在所有项目类型上的理想反应模式,将理想反应模式放入到决策表中,每一列为一个被试的理想反应模式,每一行表示所有不同的被试在同一个项目上的作答结果和对应该项目的认知属性向量(例如图2的收敛型结构自动标定决策表如表5)。
同样地,对该决策表先约简再提取规则,由RSES软件,从该决策表中共提取了8条决策规则:规则一:(atribute2=1)=>(knowledgestates=10000)规则二:(atribute2=0)&(atribute3=1)=>(knowle dgestates=11000)
规则三:(atribute2=0)&(atribute4=1)&(atribute5=1)=>(knowledgestates=11000)
规则四:(atribute3=0)&(atribute4=1)=>(knowle dgestates=11100)
规则五:(atribute4=1)&(atribute5=0)=>(knowle dgestates=11100)
规则六:(atribute3=0)&(atribute5=1)=>(knowle dgestates=11010)
规则七:(atribute4=0)&(atribute5=1)=>(knowle dgestates=11010)
规则八:(atribute4=0)&(atribute5=0)=>(knowle dgestates={11111,11110})
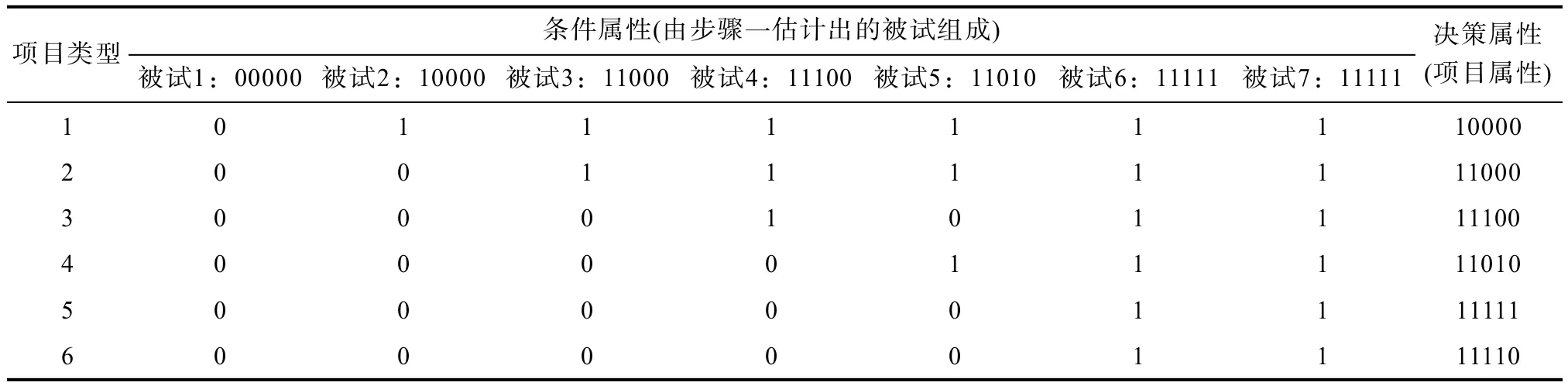
表5 5个属性收敛型结构项目认知属性自动标定决策表
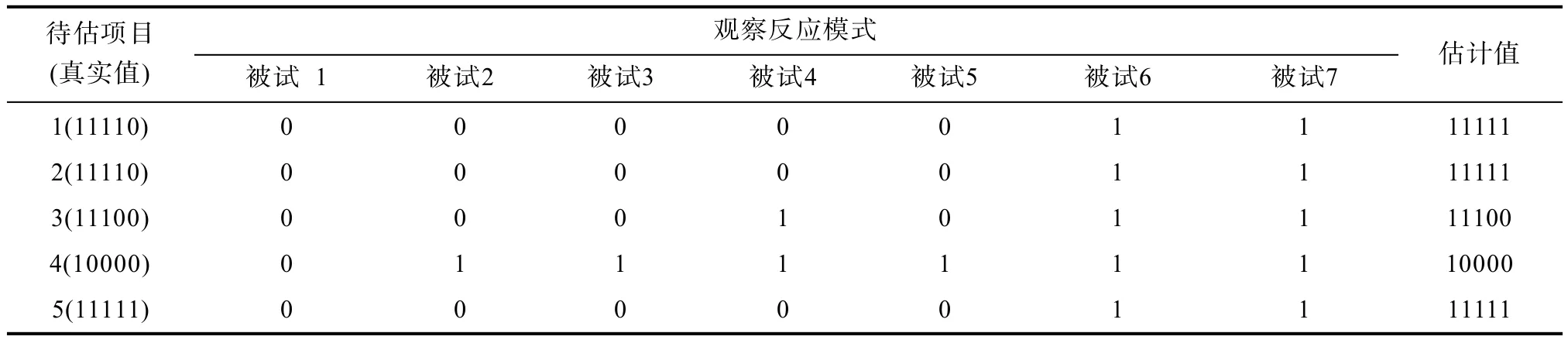
表6 利用决策规则对5个项目进行认知属性自动标定
第三步根据决策表提取的决策规则,自动标定项目认知属性。比如随机产生5个项目,这5个项目对应的真实认知属性向量分别(1,1,1,1,0)、(1,1,1,1,0)、(1,1,1,0,0)、(1,0,0,0,0)、(1,1,1,1,1),这5个项目作为待估项目,即要被自动标定的项目。由估计的被试在这5个项目上的观察反应模式及第二步提取的规则将项目进行分类,也即对项目进行认知属性自动标定。
项目认知属性的模式标定准确率和边际标定准确率采用与知识状态的模式判准率和边际判准率类似定义(陈平,辛涛,2011)。由表6看出,5个项目的认知属性自动标定,虽然其模式标定准确率为60%,即5个项目中标定对其中3个,但实际上,第一、二个项目只有第5个认知属性判错了,边际标定准确率为92%,结果还是比较理想的。
上例验证了粗糙集用于标定项目认知属性的可行性,但在实际应用中,情况会复杂得多。项目认知属性标定准确率会受到被试和项目两个来源的影响。在被试方面,作为项目认知属性标定前提条件被试知识状态的判准率,以及这些被试作答待估项目时的失误率,均会影响项目认知属性的标定准确率;就项目而言,项目认知属性越多,认知属性的层级结构越松散(杨淑群等,2008),认知属性的组合形式就越多,与作答反应之间的关系就会越复杂,这些都会增加项目认知属性标定的难度。但以上这些因素会在何种程度上对项目认知属性标定准确率产生影响,需要进一步的实证研究。
3 研究1:被试知识状态判准率和作答失误率对项目认知属性自动标定准确性的影响
基于上述分析,研究1首先采用Monte Carlo模拟研究被试估计判准率和作答失误率对项目属性自动标定的影响。每种情况做30次实验。本研究中,粗糙集进行项目认知属性标定在RSES软件中进行,所有实验都在CPU为3.20GHz,RAM为2Gb的105-5238CN型HP一体机上运行。
3.1 方法
固定认知属性个数为5,考虑发散型结构(如图3),其知识状态有11种,每种知识状态分配5人,被试共55人(考虑课堂情境),选取认知属性向量为10000,11000,10100,10110,11100,11110,10111,11111各一题作为待估项目。设被试知识状态估计判准率(记为PMR)分别为0.9、0.8、0.7三个水平,失误率(s)分别为0.05、0.10、0.15、0.2、0.25,共有3×5种情况。其中,被试知识状态估计判准率产生方法:根据被试人数(N人)与知识状态的真值,随机选取N×(1-PMR)个被试,将其真值进行修改;观察反应模式的产生办法:根据设定的被试、施测项目及各被试的理想反应模式,模拟被试的观察反应模式,由设定的s,针对每个被试在每个项目上的期望作答,假设某个被试某个题目上的理想反应得分是x(x=0或1),产生服从(0,1)上均匀分布的一个随机数r,如果r>1-s,就将其变为1-x,;如果r≤1-s,则在该题上的理想反应就是观察反应。

图3 5个和8个认知属性的发散型结构
3.2 结果
每次试验的估计过程耗时不到2秒。表7为30次实验中项目认知属性自动标定的模式标定准确率的均值与标准差。从表中可以看出,实验结果令人满意,模式标定准确率的值较高,其标准差较小。这两者的变化趋势:当被试知识状态估计判准率越低,则模式标定准确率越低,而标准差无明显变化规律;作答的失误率越高,模式标定准确率越低,其标准差越高;当被试知识状态判准率较高、作答失误率较低时,模式标定准确率是非常高的,如,被试知识状态判准率0.9,失误率0.05时,项目认知属性的模式标定准确率高达100%,且标准差达到0。这些结果和预期完全一致。

表7 各种项目认知属性自动标定的模式标定准确率均值与标准差
为了能更细致地说明被试判准率与作答失误率对模式标定准确率的影响,图4标记出失误率为0.05、0.1、0.15的30次模拟结果,详细说明在不同作答失误率和被试判准率条件下,模式标定准确率变化趋势。从30次模拟结果可以看出:当失误率为0.05,被试判准率为0.9时,模式标定准确率均为1,随着被试判准率下降,有个别模拟结果在0.9左右,而大部分还是维持在1(图4(a));当失误率为0.1,被试判准率为0.9时,大多数模式标定准确率还是维持在1,极个别低于1,被试判准率为0.8时的估计结果明显大于被试判准率为0.7的结果(图4(b));当失误率为0.15,则所有估计结果均有所下降(图4(c));失误率为0.2和0.25时,模式标定准确率下降更快,这里不予列出。
表8为30次实验中认知属性边际标定准确率的均值与标准差。其变化趋势与认知属性模式标定准确率基本一致。从认知属性边际标定准确率的绝对值来看,随着失误率升高,边际标定准确率降低,其标准差略有升高;随着被试判准率下降,边际标定准确率呈现下降趋势,其标准差无明显变化趋势;随着失误率降低、被试判准率升高,边际标定准确率上升很快,绝对值很高,如失误率为0.05被试判准率为0.9条件下,边际标定准确率达到1,其标准差为0,即便是失误率为0.25被试知识状态判准率为0.7的情况下,认知属性边际标定准确率也高达0.8975,标准差也只有0.0571。
图5为失误率为0.05、0.1、0.15的30次边际标定准确率的模拟结果。从30次模拟结果可以看出:基本上,当失误率分别为0.05、0.1、0.15时,边际标定准确率变化与模式标定准确率的变化一致,只是边际标定准确率的绝对值比模式标定准确率要高很多。同样地,失误率为0.2和0.25时,边际标定准确率下降更快,这里不予列出。

图4(a) 失误率为0.05时30次认知属性模式标定准确率结果

图4(b) 失误率为0.1时30次认知属性模式标定准确率结果
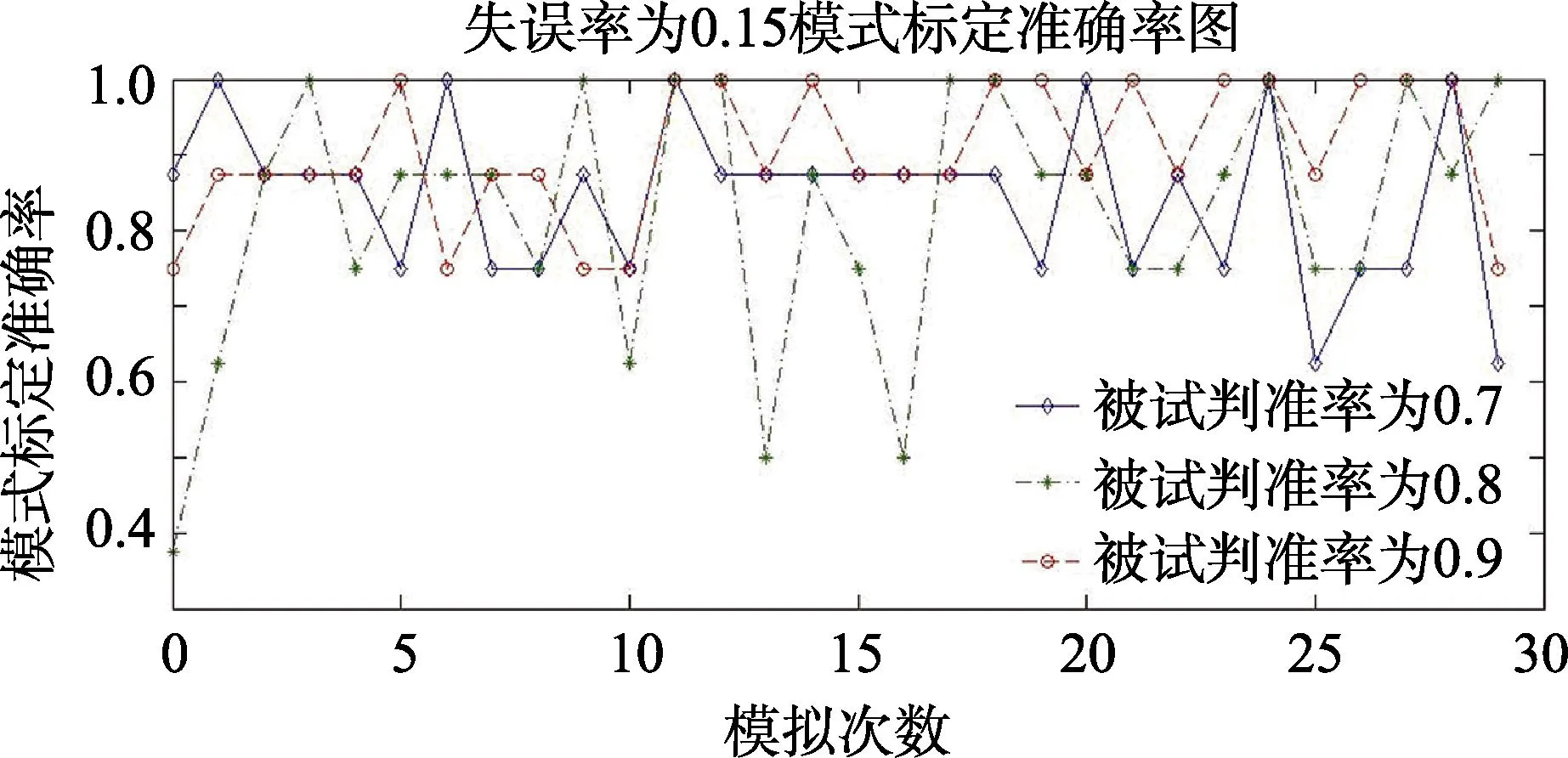
图4(c) 失误率为0.15时30次认知属性模式标定准确率结果

表8 各种项目认知属性自动标定的认知属性边际标定准确率均值与标准差
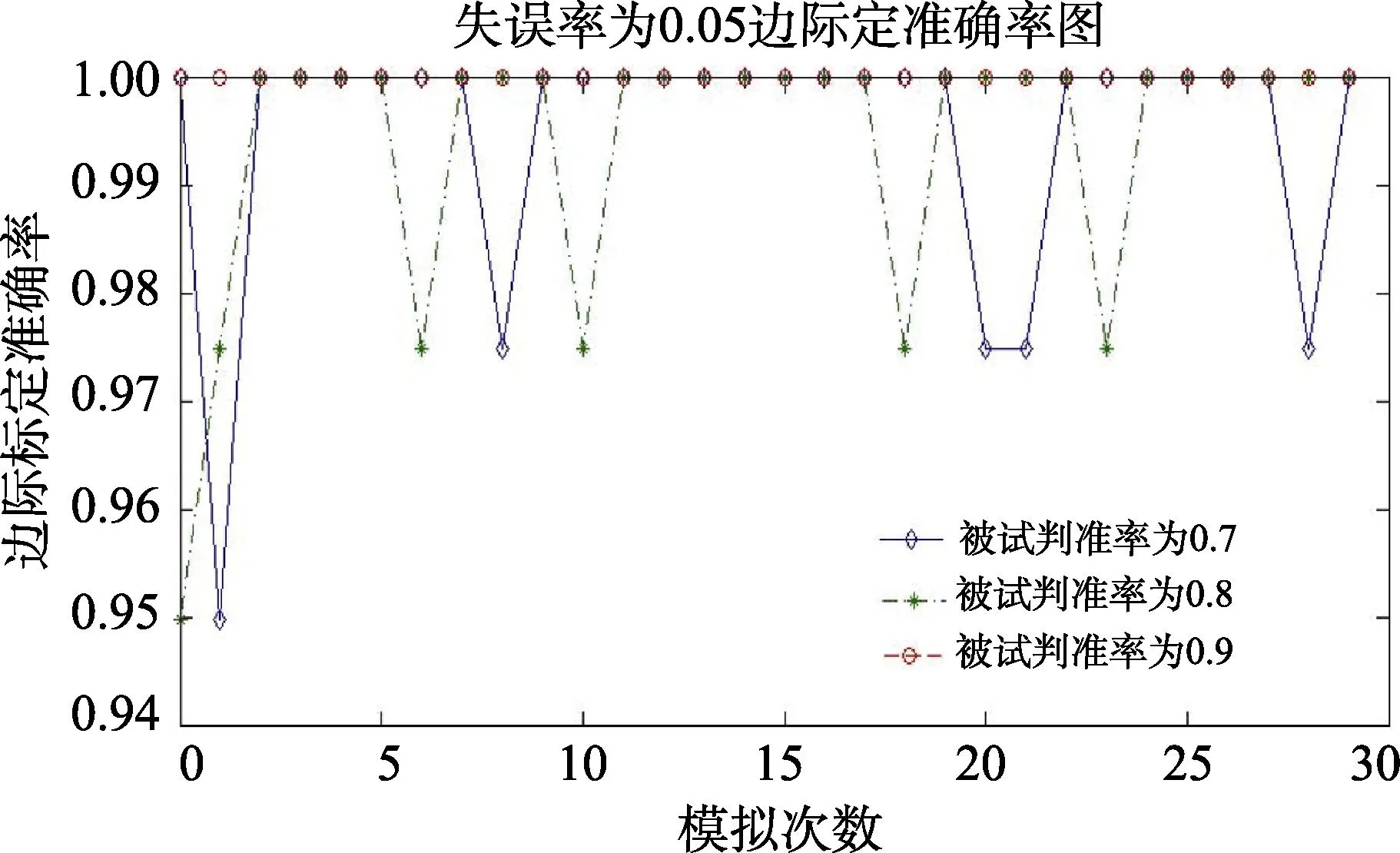
图5(a) 失误率为0.05时30次认知属性边际标定准确率结果
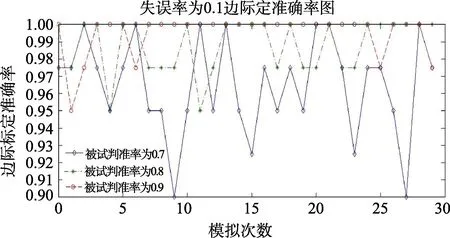
图5(b) 失误率为0.1时30次认知属性边际标定准确率结果

图5(c) 失误率为0.15时30次认知属性边际标定准确率结果
4 研究2:认知属性个数对项目认知属性自动标定的影响
项目认知属性个数是影响认知诊断的另一个重要因素,研究2进一步考察项目认知属性个数对项目认知属性自动标定的影响。预期结果是认知属性数目越多,标定准确率越低。
4.1 方法
固定被试知识状态判准率为0.9,失误率为0.15,认知属性个数K为3~8个,同样考虑发散型结构。如图3,图中8个认知属性的发散型结构,其他认知属性个数的发散型结构是8个认知属性发散型结构的一部分(5个认知属性的除外),比如3个认知属性的发散型结构为其中1~3个认知属性所组成的,4个认知属性的发散型结构为其中1~4个认知属性所组成的,以此类推。已知每种认知属性个数条件下,在发散型结构的项目类型中,随机选取待标定项目个数为K。被试55人平均分配到各种认知属性掌握模式之中;被试的认知属性掌握模式,不能均分的,随机指派一个掌握模式。每种情况做30次实验。
4.2 结果
每次估计耗时不到2秒。表9为30次实验中认知属性模式标定准确率的均值及其标准差,从该表可知,模式标定准确率随认知属性个数的增加而降低,当认知属性个数在6个以下时,认知属性模式标定准确率不低于90%。此后,每增加一个认知属性,认知属性模式标定准确率降低10个百分点左右,甚至更多。标准差无明显变化趋势。

表9 认知属性个数不同时的项目认知属性模式标定准确率均值及其标准差
表10为30次实验中认知属性边际标定准确率的均值及其标准差,从该表可知,认知属性标定的边际标定准确率随认知属性个数的增加而降低,但下降的速度较慢,即便是认知属性个数为8个的情况,认知属性边际标定准确率仍然高达0.8875。其标准差的值比模式标定准确率标准差的值低些。

表10 认知属性个数不同时的项目认知属性边际标定准确率均值及其标准差
5 研究结论与讨论
本研究首次将粗糙集运用于认知诊断中项目属性自动标定问题,通过研究结果验证了粗糙集在认知诊断中的可行性,同时解决了纸笔测验的项目属性自动标定问题,并取得满意结果。
5.1 粗糙集做认知诊断过程
采用粗糙集进行项目属性自动标定流程:构建决策表(引入IRP)→属性约简→提取决策规则(引入ORP)→被试分类。在决策表中使用理想反应模式,以该数据作为一个标准,然后用观察反应模式与之对比,进行分类。值得注意的是:从决策表中提取规则是基础,分类是目的,如果没有由期望反映模式提取的规则,则根据提取规则将观察反应模式分类这一过程便不能实现。
5.2 项目属性自动标定结果
本研究不仅在理论上论证了粗糙集进行项目认知属性标定的可行性,而且以发散结构为例,进行了模拟研究,探讨了被试估计准确率、被试在待估项目上的失误率和认知属性个数对项目认知属性自动标定准确率的影响,并取得了预期结果:
(1)考察被试知识状态估计准确率和作答失误率对项目认知属性自动标定准确率的影响
从被试估计判准率和作答失误率对项目认知属性自动标定准确率影响的模拟数据可以看到,被试估计判准率越低或作答的失误率越高,则模式标定准确率和边际标定准确率越低。从绝对值来看,当被试判准率较高、作答失误率较低时,模式标定准确率是非常高的,如被试判准率为0.9,作答失误率为0.05时,模式标定准确率为100%;即使被试判准率为0.7,作答失误率为0.05时,模式标定准确率也高达97%以上;失误率为0.15时,被试判准率为0.7,模式标定准确率为84%以上。对于边际标定准确率而言,即便是在被试估计判准率为0.7,失误率为0.25的情况下,认知属性边际标定准确率仍然高达89.75%。模式标定准确率与边际标定准确率的标准差都较小,但边际标定准确率的标准差更小一些。
(2)考察认知属性个数对项目认知属性自动标定准确率的影响
如所预测的结果一样,认知属性个数越多,模式标定准确率和认知属性边际标定准确率则越低。当认知属性个数在6个以下时,模式标定准确率均在90%以上,此后,随着属性个数的增加,模式标定准确率下降10个百分点左右(或者更多),如6个属性,模式标定准确率为86%左右;7个属性,模式标定准确率下降为77%左右。而认知属性边际标定准确率相对来说一直很高,7个属性及以下,边际标准率为94%以上;8个属性,认知属性边际标定准确率仍然高达0.8875。这些模拟结果在一定程度上表明了粗糙集用于项目认知属性自动标定是可行的,且结果理想。同样地,模式标定准确率与边际标定准确率的标准差都较小,边际标定准确率的标准差相对更小一些。
5.3 粗糙集方法运用于项目属性自动标定的优点
认知诊断要真正发挥其有助于补救性教学的作用,就需要重视形成性评估(formative assessment),需要走进课堂,进行课堂评估(classroom assessment)。但低成本、不受被试样本容量的限制、诊断反馈及时等三个特点,是认知诊断进入课堂的必备要件,而这些,也正是粗糙集的优点所在(Tang&Ding,2012),并在本研究中再一次得到了印证。
(1)成本低
到目前为止,项目认知属性自动标定,主要采用在线计算机化自适应测验的方式进行(Chen,Xin,Wang,&Chang,2012;陈平,辛涛,2011;汪文义等,2011)。由于计算机自适应测验在题库建设及硬件条件方面的要求较高,采用计算机化自适应测验的方式进行认知属性标定,成本过高。采用粗糙集进行项目认知属性标定,可适用于纸笔测验的情况,这使得题库建设及硬件条件方面的成本门槛大为下降。
(2)样本量要求低
从研究1和研究2可以看出,粗糙集用于项目认知属性自动标定,对被试数量的门槛要求是非常低的,样本容量一律为55人,即便是有八个认知属性的情况,估计结果的认知属性边际标定准确率也非常高,粗糙集的这一优点是包括CD-CAT在内的许多其他认知诊断方法所无法比拟的。55人,大抵相当于我国许多学校一个自然班的人数,粗糙集的运用,对于帮助认知诊断测验真正进入课堂,是非常重要的。
(3)反馈及时
粗糙集用于项目认知属性标定的速度也非常快,几秒钟即可出结果,从模拟结果来看,令人满意,进一步说明粗糙集运用的可行性。
另外,由于有现成的粗糙集软件RSES可以使用,实际工作者可以不必明白粗糙集的原理,就可以获得相应的结果,这有利于推广基于粗糙集的认知诊断。
5.4 关于粗糙集
粗糙集是一个强大的数据分析工具。它能够表达和处理不完全、不精确、不确定的定量或定性信息;能够在保留关键信息的前提下对数据进行简化,大大降低知识的表达空间维数,并求得知识的最小表达;能够识别并评估数据之间的依赖关系,揭示出概念简单化的模式;能够从经验数据中获取易于证实的规则知识(吴今培,孙德山,2006)。Duda,Hart和Stork(2000)认为,如果类别是用实体间的一般关系所刻画的,而非一些具体示例,那么基于规则来设计分类器的想法将很吸引人。基于规则的方法是人工智能算法不可或缺的一部分,但在模式识别中应用的不多。规则的最大优点是其容易被解释,所以可应用于数据库中,在那里,信息常被编码成实体间的关系。采用粗糙集做认知诊断,有其优势,但也有不足之处。这种方法的缺点之一是缺少自然概率的概念,因而,当问题中存在较大噪声或很大贝叶斯误差时,规则的运用多少有些困难。
5.5 造成分类误差可能原因及可进一步研究的问题
(1)因粗糙集缺乏概率的概念,所以当数据存在较大噪声时,则分类判准率会受到影响。因此,在今后,可以继续考虑将粗糙集与概率相结合的课题。同时,采用粗糙集做认知诊断,粗糙集中的决策表实际上可以看作一个无参数的认知诊断模型,具有无需项目参数的优势。在分类过程中,使用决策表涉及到属性约简和规则提取,而这两部分一直是粗糙集理论的主要课题,也是影响后面分类的关键所在,许多学者一直致力于研究如何能最大化地减少条件属性,提炼出最简洁的规则。将粗糙集运用在认知诊断中同样也存在着这两个问题,如何能改进现有的约简算法和提取规则方法,以期能够进一步提高分类准确率值得深入探讨。
(2)在认知诊断中,若项目设计不合理也会极大地影响判准率,因此,测验蓝图设计的问题不容忽视。在本研究中,所有施测项目都是随机选取,忽略了项目设计。丁树良、杨淑群和汪文义(2010),以及丁树良、汪文义和杨淑群(2011)提出在施测项目中放入可达阵可提高判准率,今后,可进一步讨论在施测项目中放入可达阵对项目属性标准率的影响。
(3)本研究只考察了单策略的情景,单策略和多策略的使用正确与否会直接影响到判准率(涂冬波,蔡艳,戴海琦,丁树良,2012),粗糙集方法能否实现诸如多策略多成分潜在特质模型的功能,可进行深入探讨。
(4)本研究是在Leighton等(2004)的理论框架下对项目属性自动标定的模拟,将独立结构排除在基本的属性层级结构之外,但也有研究者在模拟研究中只讨论独立结构,因此用粗糙集对独立结构做认知诊断也值得研究。
American Psychological Association,American Educational Research Association,&National Council on Measurements Used in Education.(1954).Technical Recommendations for Psychological Tests and Diagnostic Techniques.Psychological Bulletin,51
(2,Pt.2),1-38.Anastasi,A.,&Urbina,S.(1997).Psychological testing
(7th ed).New Jersy:Prentice Hall.Chang,H.-H.(2014).Psychometrics behind computerized adaptive testing.Psychometrika,
In Press.Chen,P.,&Xin,T.(2011).Developing on-line calibration methods for cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica,43
(6),710–724.[陈平,辛涛.(2011).认知诊断计算机化自适应测验中在线标定方法的开发.心理学报,43
(6),710–724.]Chen,P.,Xin,T.,Wang,C.,&Chang,H.-H.(2012).Online calibration methods for the DINA model with independent attributes in CD-CAT.Psychometrika,77
(2),201–222.Cronbach,L.J.,&Meehl,P.E.(1955).Construct validity in psychological tests.Psychological Bulletin,52
(4),281–302.DeCarlo,L.T.(2011).On the analysis of fraction subtraction data:The DINA model,classification,latent class sizes,and the Q-Matrix.Applied Psychological Measurement,35
(1),8–26.Ding,S.L.,Luo,F.,Cai,Y.,Lin,H.J.,&Wang,X.B.(2008).Complement to Tatsuoka’s Q matrix theory.In C.Tokyo,Japan.A.Okada,T.Imaizumi,&T.Hoshino(Eds.),New trends in psychometrics
(pp.417–424).Universal Academy Press.Ding,S.L.,Wang,W.Y.,&Yang,S.Q.(2011).The design of cognitive diagnostic test blueprints.Psychological Science,34
(2),258-265.[丁树良,汪文义,杨淑群.(2011).认知诊断测验蓝图的设计.心理科学,34
(2),258–265.]Ding,S.L.,Yang,S.Q.,&Wang,W.Y.(2010).The importance of reachability matrix in constructing cognitively diagnostic testing.Journal of Jiangxi Normal University(Natural Sciences Edition),
34(5),490–494.[丁树良,杨淑群,汪文义.(2010).可达矩阵在认知诊断测验编制中的重要作用.江西师范大学学报(自然科学版),34
(5),490–494.]Ding,S.L.,Zhu,Y.F.,Lin,H.J.,&Cai,Y.(2009).Modification of Tatsuoka’s Q matrix theory.Acta Psychologica Sinica,41
(2),175–181.[丁树良,祝玉芳,林海菁,蔡艳.(2009).Tatsuoka Q矩阵理论的修正.心理学报,41
(2),175–181.]Duda,R.O.,Hart,P.E.,&Stork,D.G.(2000).Pattern classification
.New York:Wiley-Inter science.Frederiksen,N.,Mislevy,R.J.,&Bejar,I.I.(1993).Test theory for a new generation of tests
.Hillsdale,N.J.:L.Erlbaum Associates.Gierl,M.J.,&Leighton,J.P.(2007).Directions for future research in cognitive diagnostic assessment.InJ.P.Leighton&M.J.Gierl(Eds.),Cognitive diagnostic assessment for education:Theory and applications
(pp.341–352).New York:Cambridge University Press.Huff,K.,&Goodman,D.P.(2007).The demand for cognitive diagnostic assessment.In:J.P.Leighton&M.J.Gierl(Eds.),Cognitive diagnostic assessment for education:Theory and applications
(pp.19–60).New York,NY,US:Cambridge University PressKuo,C.L.(2009).Item dynamic incremental reduction algorithm of item response system
(Unpublished master’s thesis).Asia University.[郭昭麟.(2009).试题扩增动态约简算法
(硕士学位论文).亚洲大学.]Leighton,J.P.,&Gierl,M.J.(Eds.).(2007).Cognitive diagnostic assessment for education:Theory and applications
.New York:Cambridge University Press.Leighton,J.P.,Gierl,M.J.,&Hunka,S.M.(2004).The attribute hierarchy method for cognitive assessment:A variation on Tatsuoka's rule-space approach.Journal of Educational Measurement,41
(3),205–237.Liu,J.C.,Xu,G.J.,&Ying,Z.L.(2012).Data-driven learning of Q-matrix.Applied Psychological Measurement,36
(7),548–564.Liu,J.C.,Xu,G.J.,&Ying,Z.L.(2013).Theory of self-learning$Q$-matrix.Bernoulli,19
(5A),1790–1817.Liu,L.L.(2010).Item and user dynamic incremental reduction algorithm of item response system based on rough set theory
(Unpublished master’s thesis).Asia University.[刘丽铃.(2010).基于粗糙理论之试题及受试者扩增动态约简算法
(硕士学位论文).亚洲大学.]McGlohen,M.K.(2004).The application of cognitive diagnosis and computerized adaptive testing to a large-scale assessment
(Unpublished doctorial dissertation).University of Texas at Austin.Pawlak,Z.(1991).Rough sets:Theoretical aspects of reasoning about data
.Dordrecht:Kluwer Academic Publishers.Quellmalz,E.S.,&Pellegrino,J.W.(2009).Technology and testing.Science,323
(5910),75–79.Shi,Z.Z.(2002).Knowledge discovery
(p.143).Beijing:Tsinghua University Press.[史忠植.(2002).知识发现
(p.143).北京:清华大学出版社.]Tang,X.J.,&Ding,S.L.(2012).Application of rough set theory in cognitive diagnosis
.Assessment and Evaluation,International Journal of Psychology,47
(sup1),15–15.Tatsuoka,K.K.(1990).Toward an integration of item-response theory and cognitive error diagnosis.In N.Frederiksen,R.Glaser,A.Lesgold,&M.G.Shafto(Eds.),Diagnostic monitoring of skill and knowledge acquisition
(pp.453–488).Hillsdale,NJ:Lawrence Erlbaum Associates.Tatsuoka,K.K.(1995).Architecture of knowledge structures and cognitive diagnosis:A statistical pattern recognition and classification approach.In P.D.Nichols,S.F.Chipman,&R.L.Brennan(Eds.),Cognitively diagnostic assessment
(pp.327–359).Hillsdale,NJ:Lawrence Erlbaum Associates.Tatsuoka,K.K.(2009).Cognitive assessment:An introduction to the rule space method
.New York:Taylor&Francis Group.Tu,D.B.,Cai,Y.,Dai,H.Q.,&Ding,S.L.(2012).A new multiple-strategies cognitive diagnosis model:The MSCD method.Acta Psychologica Sinica,44
(11),1547–1553.[涂冬波,蔡艳,戴海琦,丁树良.(2012).一种多策略认知诊断方法:MSCD方法的开发.心理学报,44
(11),1547–1553.]Wang,W.Y.,Ding,S.L.,&You,X.F.(2011).On–line item attribute identification in cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica,43
(8),964–976.[汪文义,丁树良,游晓锋.(2011).计算机化自适应诊断测验中原始题的属性标定.心理学报,43
(8),964–976.]Wu,J.P.,&Sun,D.S.(Eds).(2006).Modern data analysis
(p.247).Beijing:Machinery Industry Press.[吴今培,孙德山.(编).(2006).现代数据分析
(p.247).北京:机械工业出版社.]Yang,S.Q.,Cai,S.Z.,Ding,S.L.,Lin,H.J.,&Ding,Q.L.(2008).Augment algorithm for reduced Q-matrix.Journal of Lanzhou University(Natural Sciences),44
(3),87–91,96.[杨淑群,蔡声镇,丁树良,林海菁,丁秋林.(2008).求解简化Q矩阵的扩张算法.兰州大学学报(自然科学版),44
(3),87–91,96.]You,X.F.,Ding,S.L.,&Liu,H.Y.(2010).Parameter estimation of the raw item in computerized adaptive testing.Acta Psychologica Sinica,42
(7),813–820.[游晓锋,丁树良,刘红云.(2010).计算机化自适应测验中原始题项目参数的估计.心理学报,42
(7),813–820.]Yu,J.Y.(2008).Application of rough set and neural networks in psychological Measurement.Acta Psychologica Sinica,40
(8),939–946.[余嘉元.(2008).粗糙集和神经网络在心理测量中的应用.心理学报,40
(8),939–946.]Zhang,W.X.,Wu,W.Z.,Liang,J.Y.,&Li,D.Y.(2001).The theory and methods of rough set
.Beijing:Science Press.[张文修,吴伟志,梁吉业,李德玉.(2001).粗糙集理论与方法
.北京:科学出版社.]