波浪扰动下的小型潜射导弹出水动力学建模与仿真*

张重先

(中国航天科工二院， 北京　100039)



波浪扰动下的小型潜射导弹出水动力学建模与仿真*

张重先

(中国航天科工二院， 北京100039)

摘要：运用Morison公式，提出波浪扰动作用下，考虑弹体运动与波浪耦合的导弹出水过程动力学模型，并对小型潜射导弹的出水过程进行仿真和分析。以弹体姿态变化为例，研究弹体运动与波浪间的耦合关系对波浪扰动作用的影响，分析海情等级、波浪相位、出水速度、出水姿态角等因素对导弹出水过程的影响。结果表明，考虑弹体运动与波浪间耦合关系的出水动力学模型更加准确；潜射导弹的小型性和快速出水特性有利于降低波浪对导弹出水姿态的影响；对快速出水的潜射导弹，波浪扰动分析时须考虑海情等级、出水时间和波浪相位的影响。

关键词：潜射导弹；波浪扰动；Morison公式；动力学建模

出水阶段是潜射导弹特有的飞行阶段，是导弹依靠惯性或利用水下发动机的推力上升，直至弹身完全出水的过程。该阶段，导弹姿态和弹道将受到波浪的影响，从而偏离设计状态，甚至导致导弹飞行不稳定或倾覆。分析波浪对潜射导弹出水过程的影响是潜射导弹能否成功发射的关键。

目前，波浪对航行体扰动的研究主要针对舰船补给、海上吊装及海洋平台定位等方面[1-2]，对导弹出水的波浪扰动方面研究尚处于起步阶段。权晓波、李平金等对波浪引起的导弹横移进行了研究[3-4]。田兵、崔奇伟等对波浪引起的导弹出水姿态偏差进行了计算[5-6]。刘曜对航行体出水弹道参数进行预报[7]。目前国内外的研究主要通过计算流体力学方法获得导弹出水过程的压力场分布，进而得到波浪对潜射导弹运动的影响，该方法计算周期较长、过程复杂。

Morison公式是Morison，O′Brien和Johnson于1950年提出的波浪力计算公式，适用于海底固定的竖直小型刚性圆柱构件，目前在海洋工程中有广泛应用。Kurian、项贻强等分别计算了海洋平台及海底隧道的波浪载荷，显示出Morison公式良好的精度[8-9]。Huang对固定的小直径圆管的波浪力进行了计算[10]。目前对Morison公式的研究主要针对海上固定构件或大型构件，此类构件抗波浪的能力较强，由波浪导致的运动及姿态变化较小，因而可以忽略波浪与构件运动的耦合关系。而对于潜射导弹一类的小型、快速移动航行器，以上研究方法并不适用。

1潜射导弹出水运动模型

1.1　动力学方程

与传统导弹飞行力学不同，由于导弹出水过程的航行介质主要为水，非定常流体动力引起的附加质量力的影响不可忽略。由于浮心是不变的导弹形状对称中心，导弹出水的动力学方程建立于弹体坐标系中，原点位于导弹浮心。设导弹受到重力G、浮力B、流体动力F、波浪力W、发动机推力T，导弹质量为m，转动惯量为Jij，速度在弹体坐标系中的分量为vx，vy，vz，角速度为ωx，ωy，ωz，附加质量为λij，质心在弹体坐标系中的位置为xc，yc，zc，忽略导弹惯性积及发动机推力偏心，则导弹运动的动力学方程[11]为：

(1)

其中，

1.2　运动学方程

对于垂直发射出水的潜射导弹，采用四元数方法建立其运动学方程。

(2)

为保持四元数的正交性，每次迭代求解后需要对四元数做规范化处理。

2潜射导弹波浪扰动模型

2.1　波浪模型

假设波浪为有势运动，且波幅为一有限量。设波数为k，波浪传播速度为c，波浪相位为θ，水深为d，则波浪速度势Φ满足：

(3)

其中，

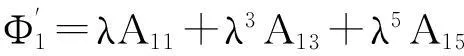
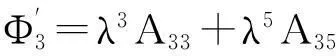
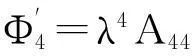
式中：比值系数λ=ak,a为与波相关的常数；Aij可由已有表格确定。

2.2　波浪力与波浪力矩模型

由Morison公式，固定在海底的竖直圆柱体微段dz上的波浪力dF分为波浪拖曳力和波浪惯性力，可表示为：

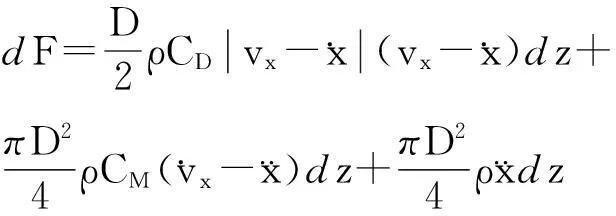
(4)

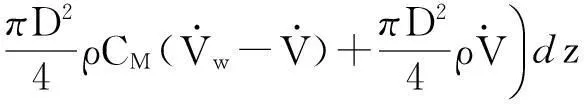
其中，V=Vm+ω×r，

3数值仿真与计算结果

3.1　波浪力计算模型验证

对文献[12]中的算例进行计算，其与本文方法的结果对比如图1、图2所示。

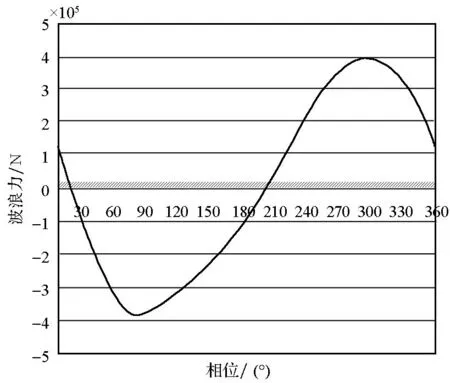
(a)文献[12]波浪力(a) Wave force of references[12]

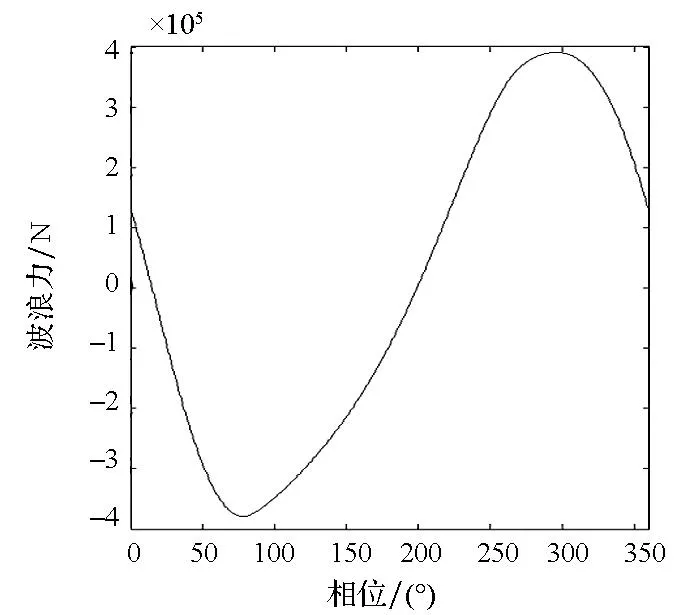
(b) 本文波浪力(b) Wave force of this article图1　波浪力计算结果Fig.1　Calculation result of wave force

(a) 文献[12]波浪力矩(a) Wave moment of references[12]

(b) 本文波浪力矩(b) Wave moment of this article图2　波浪力矩计算结果Fig.2　Calculation result of wave moment

由仿真得到的最大波浪力计算结果与文献[12]的相对偏差为1.03%，最大波浪力矩相对偏差为0.86%，仿真结果吻合较好，表明上述模型可对水中航行体的波浪扰动作用进行准确计算。

3.2　波浪对潜射导弹出水过程的影响

以水下10m为导弹初始位置、导弹弹体完全出水为终止时刻，取3级海情浪高H=1.25m，波浪周期T=6.7s；5级海情浪高H=4.0m，波浪周期T=7.9s，对波浪干扰下的潜射导弹出水过程进行仿真计算。由于篇幅所限，仅列出导弹出水姿态变化仿真结果。

波浪初始相位0°，导弹初始俯仰角90°，初速度20m/s，不同海情下波浪对导弹俯仰角的影响见图3。

图3　典型海情下出水过程俯仰角Fig.3　Pitching angle of water-exit course　under typical sea conditions

对于典型波浪初始相位，对5级海情、初始俯仰角90°、初速度20m/s情况下的导弹出水过程俯仰角进行计算，结果如图4所示。

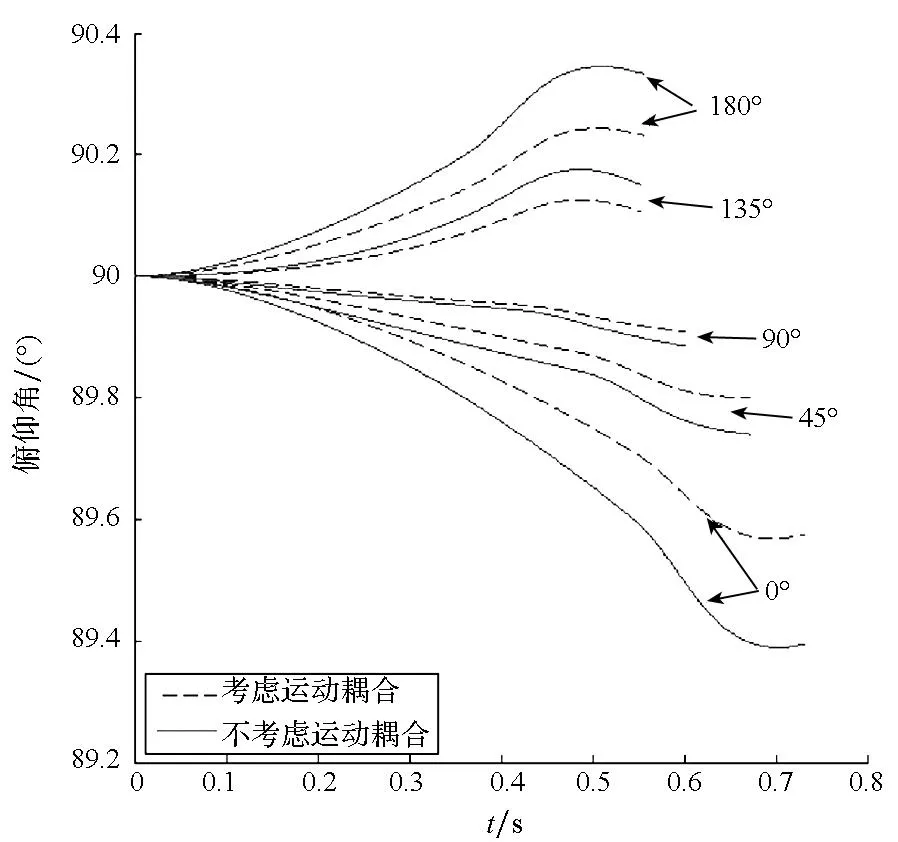
图4　典型波浪初始相位下出水过程俯仰角Fig.4　Pitching angle of water-exit course 　　　under typical initial wave phases

对于典型导弹初始速度，对5级海情、导弹初始俯仰角90°、0°波浪初始相位下的导弹出水过程俯仰角进行计算，结果如图5所示。

图5　典型导弹初速度下出水过程俯仰角Fig.5　Pitching angle of water-exit course under　typical initial velocity of missile

对于典型导弹初始俯仰角，对5级海情、导弹初速度20m/s、0°波浪初始相位下，导弹出水过程的俯仰角变化进行计算，结果如图6所示。

图6　典型初始俯仰角下导弹出水过程俯仰角变化Fig.6　Change of pitching angle of water-exit course under typical initial pitching angle

将导弹出水过程分为两个阶段：弹体完全浸没时，波浪载荷随导弹上升逐步增加，波浪引起的扰动也随之增加，该阶段导弹波浪扰动的变化主要由流体质点的运动速度增加引起；弹体穿越水面时，由于水、气交界面密度突变，导致导弹运动状态快速、剧烈变化，该阶段导弹波浪扰动的变化由弹体沾湿面积减小与流体质点运动速度增加共同引起。对影响波浪扰动的各因素进行分析，可得：

1)海情等级的提升增加了流体质点的运动速度，显著提升了导弹所受的波浪力和波浪力矩，从而使波浪对导弹的扰动作用更强。由以上仿真可知，5级海情下波浪引起的导弹出水姿态偏差为3级海情的4～5倍。

2)由于潜射导弹出水过程时间约为1s，小于波浪周期。因而，波浪相位对导弹波浪扰动的影响不可忽略。导弹在波峰出水时所受的波浪扰动与波谷出水时的相比将提升约4倍，同时，导弹波浪扰动的方向也随波浪相位而变化。

3)波浪对导弹出水过程的影响随导弹出水时间的增加而增加。因此，增加导弹出水速度、缩短导弹出水时间可以降低波浪对导弹出水运动的干扰。

4)从波浪与弹体运动之间的耦合关系来看，波浪扰动使导弹在波浪行进方向上产生位移、速度及加速度，同时改变导弹的俯仰角及弹道倾角，从而使弹体与流体质点间的相对运动速度及加速度减小，进而降低导弹出水过程的波浪扰动。考虑波浪与弹体运动间的耦合作用，弹体的波浪扰动影响计算结果减小约20%～30%。因此，对于质量、转动惯量较小的小型航行体而言，航行体运动对波浪扰动的影响不可忽略。同时，由于导弹运动状态的改变速度随波浪扰动的增强而加快，因此，导弹出水的波浪扰动越强，波浪与弹体运动间的耦合对波浪扰动的影响越明显。

4结论

弹体穿越水面时，波浪扰动作用加剧。海情等级与出水时间的增加会增加波浪对导弹的扰动作用；波浪相位对潜射导弹出水波浪扰动的影响不可忽略；考虑航行体运动与波浪的耦合作用后，航行体波浪扰动计算结果减小约20%～30%。波浪相位对波浪扰动的大小和方向均有影响，且影响效果最为显著。导弹弹长较短、出水速度快，可降低弹体所受的波浪力矩、缩短了导弹的出水时间。因此，导弹的小型性和快速性有利于降低波浪对潜射导弹的扰动作用。波浪对小型、快速出水的潜射导弹俯仰角的影响约为1°～2°。

参考文献(References)

[1]王晓明，尚建忠，张志雄.双浮体波浪能转换装置中重心布置对波浪能吸收影响分析[J].国防科技大学学报，2013, 35(4): 56-61.

WANG Xiaoming, SHANG Jianzhong, ZHANG Zhixiong. Effect of G．C arrangement on the power absorption in a two-body rolling WECS[J]. Journal of National University of Defense Technology, 2013, 35(4): 56-61. (in Chinese)

[2]徐小军，陈循，尚建忠.一种新型主动式波浪补偿系统的原理及数学建模[J].国防科技大学学报， 2007, 29(3): 118-122.

XU Xiaojun, CHEN Xun, SHANG Jianzhong.The principle and mathematical modeling of a new active heave compensation system[J]. Journal of National University of Defense Technology, 2007, 29(3): 118-122. (in Chinese)

[3]权晓波，孔德才，李岩.波浪模拟及其对水下航行体出水过程影响[J].哈尔滨工业大学学报， 2011, 43(3): 140-144.

QUAN Xiaobo, KONG Decai, LI Yan.Wave simulation and its effects on the exceeding water process of the underwater vehicle[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 140-144. (in Chinese)

[4]李平金，牟秀军.波浪在导弹出水过程中影响效果数值分析[J].舰船电子工程， 2010, 30(8): 159-161.

LI Pingjin, MOU Xiujun.Water in the process of wave effects missile numerical analysis[J]. Ship Electronic Engineering, 2010, 30(8): 159-161. (in Chinese)

[5]田兵，徐新琦，肖鹏飞.波浪对潜地弹道导弹出水运动的影响[J].舰船科学技术， 2009, 31(4): 81-84.

TIAN Bing, XU Xinqi, XIAO Pengfei.Wave effect on the exceeding water motion of submarine-to-ground ballistic missile[J]. Ship Science and Technology,2009, 31(4): 81-84. (in Chinese)

[6]崔奇伟，王瑞臣.基于ANSYS/LS-DYNA的波浪对潜射导弹出水姿态影响分析[J].兵工自动化， 2011, 30(1): 19-21.

CUI Qiwei, WANG Ruichen. Wave effect on gesture perforating water of submarine-launched missile[J]. Ordnance Industry Automation, 2011, 30(1): 19-21. (in Chinese)

[7]刘曜.波浪对运载器出水姿态角的影响[J].舰船科学技术， 2005, 27(3): 32-34.

LIU Yao. Wave effect on a submerged missile capsule traveling near-surface[J]. Ship Science and Technology, 2005, 27(3): 32-34. (in Chinese)

[8]Kurian V J,Ng C Y, Liew M S. Dynamic responses of classic spar platforms subjected to long crested waves: morison equation vs. diffraction theory[C]//Proceedings of 2012 International Conference on Statistics in Science, Business, and Engineering (ICSSBE), Awana Porto Malai Hotel, Langkawi, Kedah, Malaysia, 2012: 1-6.

[9]项贻强，张科乾.基于Morison方程分层积分计算悬浮隧道的波浪力[J].浙江大学学报(工学版)， 2011, 45(8): 1399-1404.

XIANG Yiqiang, ZHANG Keqian. The layered integrating method for calculating wave force of submerged floating tunnel based on Morison equation[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(8): 1399-1404. (in Chinese)

[10]Huang T, Gong W M, Dai G L. The forces on small diameter piles in wave-current field[C]//Proceedings of 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 2011:3660-3663.

[12]王茂励，赵国良. 鱼雷空间运动非线性数学模型的建立与仿真[J].系统仿真学报， 2007, 19(20): 4812-4814.

WANG Maoli, ZHAO Guoliang. Nonlinear mathematics modeling and simulation of torpedo move in space[J]. Journal of System Simulation, 2007, 19(20): 4812-4814. (in Chinese)

[11]刘英杰.自升式平台桩腿的受力分析[D].哈尔滨：哈尔滨工程大学， 2004.

LIU Yingjie. Analysis of wave loads acted on jack-up platform[D]. Harbin: Harbin Engineering University, 2004. (in Chinese)

http://journal.nudt.edu.cn

Dynamics modeling and simulation of water-exit course of small submarine-launched missile under wave disturbance

ZHANGChongxian

(The Second Academy of CASIC, Beijing 100039, China)

Abstract：Based on Morison equation, a dynamics model of water-exit missile under wave disturbance was built, which takes the coupling between wave and motion of missile into account. The water-exit motion of small submarine-launched missile was simulated and analyzed. The effects of coupling between wave and motion of missile body to wave disturbance, illustrated by change process of attitude of missile, were studied. The influences of sea condition, wave phase, velocity and attitude of missile to the motion of water-exit course were analyzed. The result indicates that the characteristics of submarine-launched, which are small in size and fast in water-exit, reduce the impact of wave to attitude of missile. In addition, the wave disturbance to high-speed water-exit missile is significantly affected by sea condition, duration of water-exit course and wave phase. The dynamic model which takes the coupling between wave and motion of missile into account is more accurate.

Key words：submarine-launched missile; wave disturbance; Morison equation; dynamics modeling

中图分类号：TJ762.4

文献标志码：A

文章编号：1001-2486(2015)06-091-05

作者简介：张重先(1988—)，男，辽宁锦州人，博士研究生，E-mail：dukebeb@163.com

基金项目：国防预研基金资助项目(9140A13030512HT20042)

收稿日期：*2015-07-18

doi:10.11887/j.cn.201506018