高阶BOC信号电离层色散效应的模拟方法*

庞　晶，刘瀛翔，唐小妹，欧　钢

(国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



高阶BOC信号电离层色散效应的模拟方法*

庞晶，刘瀛翔，唐小妹，欧钢

(国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：导航信号模拟器需要模拟电离层引起的延时和色散效应，与传统导航信号相比，新体制高阶BOC信号具有更宽的带宽，而传统导航信号的模拟方法会引入不可忽略的电离层延迟建模误差。通常情况下BOC(14,2)信号上下边带信号的电离层延迟可达到米级的差异。提出运用双边带模型的BOC信号模拟方法并进行了仿真，结果表明改进方法可以准确模拟电离层色散效应的影响。

关键词：卫星导航；BOC调制；电离层效应；信号模拟

导航信号模拟器模拟各种真实环境中用户机接收的卫星导航信号，是导航接收机功能和性能验证的重要技术手段[1]。卫星导航信号经过电离层时会发生折射，导致其传输路径会大于卫星和用户之间真实的几何距离[2]。电离层延迟作为一种重要的误差源，是影响导航接收机定位精度的关键因素之一，因此导航信号模拟器需要模拟电离层引起的信号延时和色散效应。

传统二进制相移键控(Binary Phase Shift Keying，BPSK)调制信号，其带宽较窄且频谱集中于中心频点处，信号模拟器基于单频假设，将电离层影响等效为载波相位超前和伪码相位滞后，采用动态调整载波相位和伪码相位的方法实现[3]。

新一代导航系统广泛采用的二进制偏移载波(Binary Offset Carrier，BOC)调制信号具有更宽的带宽，且频谱分散在中心频点的两侧，文献[4]表明对Galileo的AltBOC(10,5)调制信号作单频假设会引入不可忽略的电离层延迟建模误差。根据文献[5]的结论，电离层会在BOC信号的上下边带中引入不同的电离层延迟。特别是对于BOC(14,2)和BOC(15,2.5)这样的高阶BOC信号，上下边带信号中心频点的间隔接近30MHz，此时上下边带信号的电离层延迟差将达到不可忽略的程度。因此为了使用模拟信号准确评估BOC信号接收算法的性能，必须要能够准确模拟电离层在上下边带信号中引入的延迟差。

基于上述研究背景，根据BOC信号的双边带模型，提出了高阶BOC信号电离层色散效应的高精度模拟算法，并使用仿真数据验证理论分析的正确性。

1电离层色散效应模拟

导航信号模拟器模拟真实环境中用户机接收到的导航信号，由于受到卫星和用户机之间的相对运动、电离层、对流层、卫星钟差等因素的影响，到达用户机天线的信号与卫星导航信号相比，时延和信号频率均发生了变化，t时刻到达接收机信号的数学表达式为：

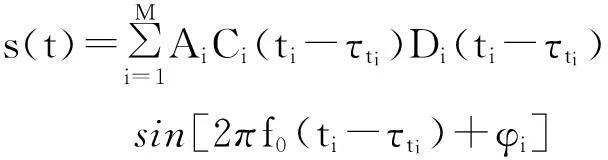
(1)

其中，A为信号幅度，C(·)为扩频码，D(·)为导航电文，τt为伪码的空间传播时延，f0为载波频率，φi为载波相位初相，M为卫星数目。

对于BPSK信号，传统电离层色散效应的模拟方法是根据电离层电子浓度总含量(Total Electron Content,TEC)计算引入的伪码相位延迟量和载波相位超前量，代入伪码时延τt和载波相位φi进行修正。

由于BPSK信号带宽较窄，使用该方法模拟电离层色散效应的精度能够满足测试要求。但是对于宽带BOC信号而言，传统的电离层色散效应模拟方法引起的码延迟误差不可忽略,下面对传统模拟方法的建模误差进行分析。

采用和BPSK信号电离层特性模拟类似的方法，将BOC信号近似为单频信号，则电离层引入的电离层在伪码相位延迟量τI和载波相位超前量θI的表达式分别为：

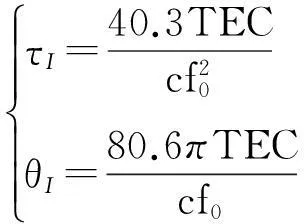
(2)

其中，c表示光速，f0为载波频率，TEC表示电离层单位面积上的电子总数，一般以TECU=1016e/m2为单位[6]。TEC在垂直方向上的取值范围为1TECU～150TECU，对应的时间延迟量的变化范围约为1ns～80ns；在低仰角时，时间延迟量一般为垂直方向上的3倍。在电离层活跃期间，TEC可以达到1000TECU[7]。

根据式(2)，对原始信号的码相位和载波相位进行修正，其表达式为：

s(t)=c(t-τ0-τI)cos(2πf0t+θ0+θI)

(3)

以BOC(14,2)信号为例，电离层不同TEC值时，传统方法与理论信号的模拟误差如图1所示，理论上的电离层色散效应是通过对理想BOC信号进行快速傅里叶变换(Fast Fourier Transform, FFT)变换转变到频域，对不同频率叠加电离层效应的影响，再通过FFT逆变转换成时域信号，得到BOC信号电离层影响的理论值。当电离层TEC值为200TECU时，传统方法在模拟上下边带信号的电离层延迟时，其模拟误差可以达到0.6m，难以准确模拟电离层的色散效应。

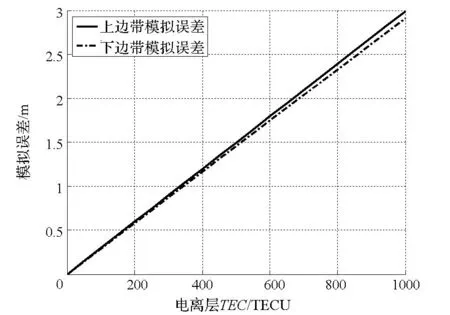
图1　高阶BOC调制上下边带信号的电离层延迟差随TEC值的变化Fig.1　Ionosphere delay of upper and lower sideband of high-order BOC modulated signals under different TEC condition

与理论信号相比，传统方法在模拟电离层对信号的影响时，得到的上下边带信号具有相同的码相位延迟量和载波相位超前量，这与真实信号之间存在差异，从而影响双边带接收算法的性能评估。

2双边带模型的高精度模拟方法

针对传统模拟方法的上述缺陷，提出了基于双边带模型的电离层延迟的高精度模拟方法。当不考虑电离层色散效应时，载波频率为f0的BOC信号可表示为：

s(t)=c(t-τ0)cos(2πf0t+θ0)

(4)

其中：θ0表示载波初相；τ0表示传输延迟；c(t)表示BOC调制后的扩频码，可改写为扩频码和方波副载波的乘积[8]：

c(t)=pn(t)sc(t)=pn(t)sgn[sin(2πfsct+ψ)]

(5)

其中：pn(t)表示频率为fc的扩频码；sc(t)表示频率为fsc的方波副载波；sgn(·)表示取符号函数；ψ表示BOC调制的相位，可取为0°或90°，分别对应为BOCs和BOCc。为了表示的简便，一般使用BOC(m,n)的形式表示方波副载波频率为m×1.023MHz，扩频码频率为n×1.023MHz的BOC调制。

由于采用了副载波调制，BOC信号的带宽远大于相同码率的BPSK信号。为了降低计算复杂度，BOC信号常采用基于信号双边带模型的接收算法来消除BOC调制信号的模糊度，该算法将BOC信号分离成两个边带信号进行处理。根据文献[9]，当不考虑多普勒频率，经过理想时延的BOC信号的双边带模型可以表示为：

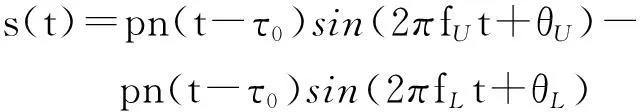
(6)

其中：fU=f0+fsc，fL=f0-fsc分别表示BOC信号上下边带信号的中心频率；θU和θL分别表示上下边带信号的载波初相，取值为θU=θ0-2πfscτ0，θL=θ0+2πfscτ0。

由于电离层折射率的高阶项的影响非常小，通常可忽略[6]。当仅考虑电离层折射率的一阶项时，BOC信号的双边带模型修正[5]为：

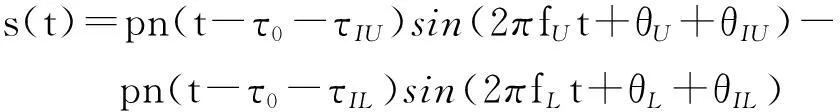
(7)

其中：τIU，τIL分别表示电离层在上下边带信号中引入的码相位延迟量；θIU，θIL分别表示电离层在上下边带信号中引入的载波相位超前量，其表达式分别为：

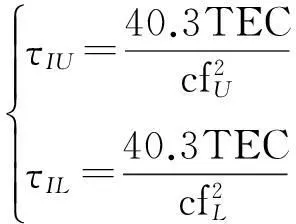
(8)

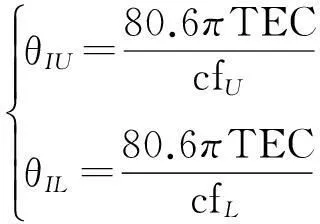
(9)

将式(8)、式(9)代入式(7)，得到的双边带模型能够准确模拟电离层在上下边带信号中引入的不同相位延迟。

3仿真验证

相关峰形状是衡量信号模拟精度的重要指标。下面比较电离层色散效应理论值和两种方法模拟得到的相关峰形状。

图2是电离层TEC值为1000TECU时，BOC(14,2)信号的相关峰形状的仿真结果。由于电离层是非线性相位滤波器，因此必然会导致相关峰的形变。

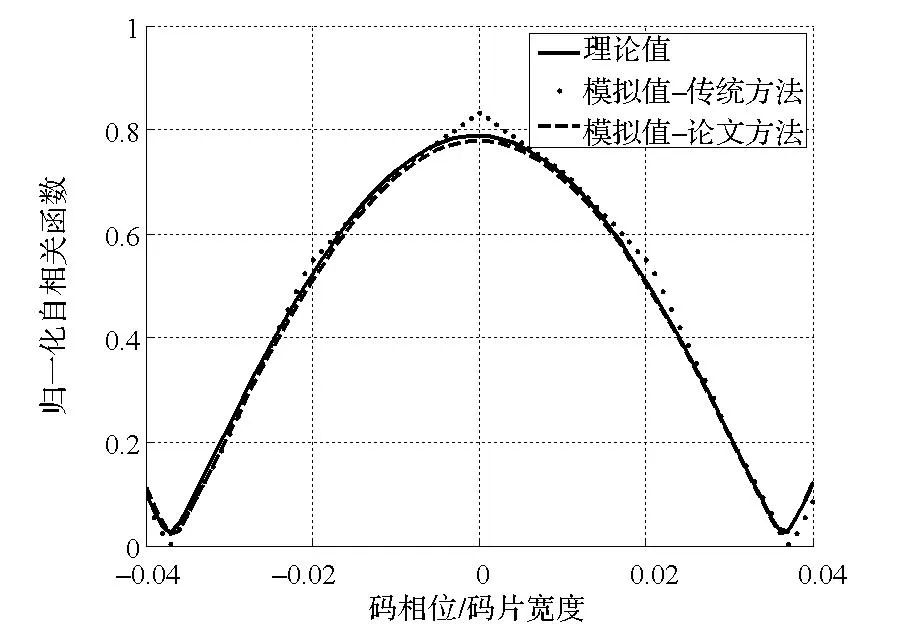
图2　BOC(14,2)信号的相关峰形状Fig.2　Auto-correlation function of BOC(14,2)

为了能够更加清晰地反映电离层影响下相关峰的形状，比较两种信号模拟算法在不同早迟码间隔下提前支路和滞后支路的幅度差，如图3所示。

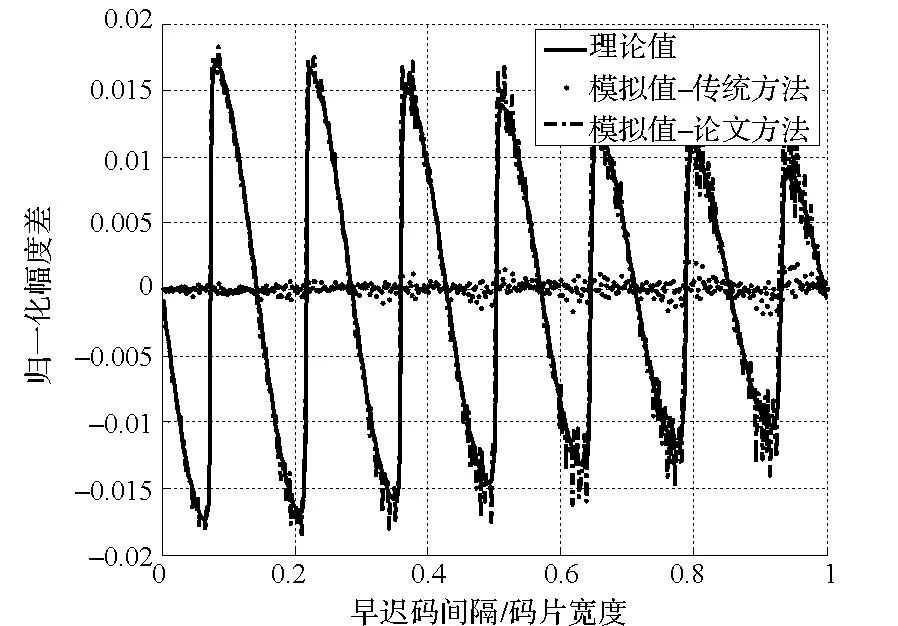
图3　不同早迟码间隔下提前支路和滞后支路幅度差Fig.3　Amplitude difference of early and late branch for traditional and proposed methods

由图2可见，论文模拟算法能够准确反映电离层色散效应所造成的相关峰变形，而传统模拟方法得到的相关峰形状是严格对称的，无法反映电离层色散特性的影响。

对于BOC信号的双边带接收而言，电离层在上下边带中引入的延迟差对其性能具有重要的影响。下面比较两种方法模拟上下边带延迟差的准确性。

在不同电离层TEC下，使用双边带技术分别接收传统方法和该方法的模拟信号，上下边带信号的码相位延迟量分别如图4和图5所示。

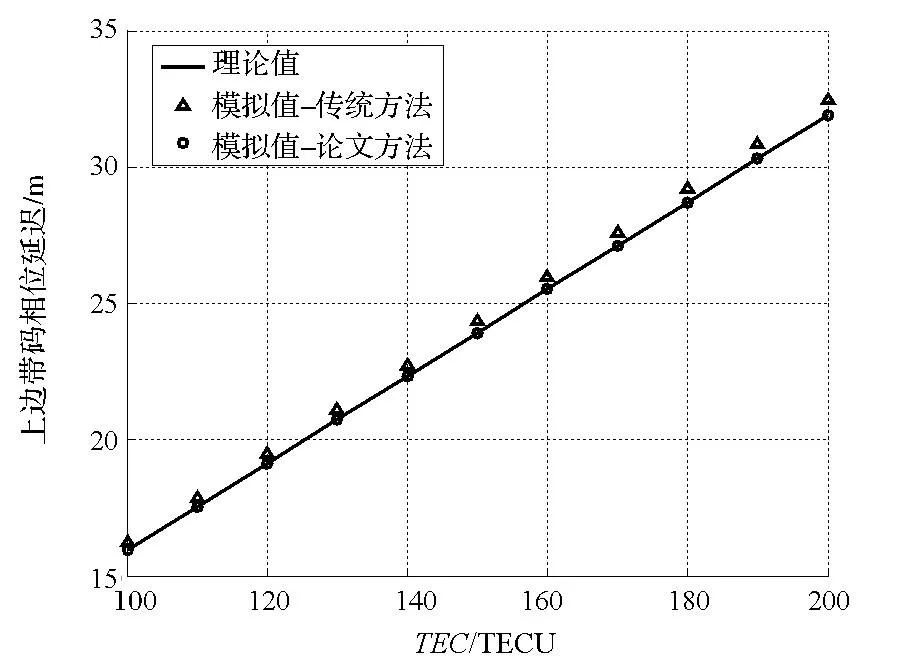
图4　上边带信号电离层延迟的模拟误差Fig.4　Ionosphere delay simulation error of upper sideband

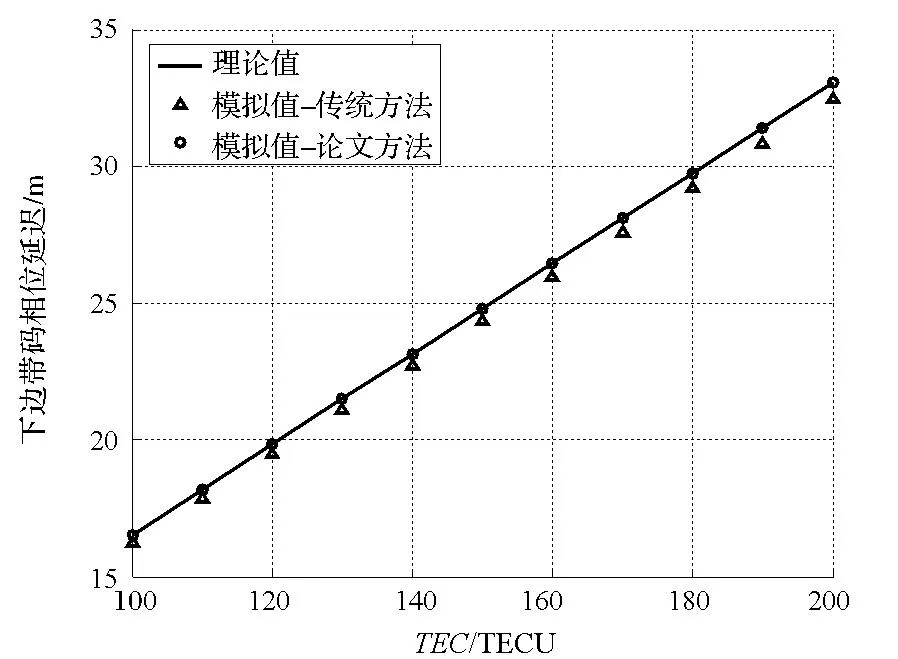
图5　下边带信号电离层延迟的模拟误差Fig.5　Ionosphere delay simulation error of lower sideband

从图4和图5可以看出，改进方法能够准确模拟电离层对高阶BOC信号上下边带信号延迟差的影响，而传统方法得到的上下边带信号的码相位延迟完全相同，无法准确模拟电离层的影响。

4结论

针对下一代卫星导航系统中的高阶BOC信号，分析了信号模拟器传统BPSK信号模拟方法在模拟电离层色散效应对高阶BOC信号影响方面的不足，提出了基于双边带模型的高精度模拟方法。仿真结果表明，该方法能够准确模拟电离层导致的相关峰形变以及上下边带信号不同的延迟差，可应用于导航模拟器实现BOC信号电离层色散效应的模拟。

参考文献(References)

[1]齐巍,常青,张其善,等.高动态信号模拟器中的多普勒模

拟算法[J].航空学报, 2008, 29(5):1252-1257.

QI Wei,CHANG Qing,ZHANG Qishan, et al. Arithmetic of doppler imulation in high dynamic signal simulator[J]. Acta Aeronautica et Astronautica Sinica, 2008,29(5):1252-1257. (in Chinese)

[2]Klobuchar J A. Ionospheric effects on GPS[J]. GPS World, 1991, 2(4):48-51.

[3]孟繁智. 高动态GPS卫星信号模拟源的关键技术研究[D].长沙：国防科学技术大学, 2004.

MENG Fanzhi. The research of the key technologies in the high dynamic GPS satellite signal simulator [D].Changsha:National University of Defense Technology, 2004. (in Chinese)

[4]Gao G X,Datta-Barua S, Walter T, et al, Ionosphere effects for wideband GNSS signals [C]// Proceedings of the 63rd Annual Meeting of the Institute of Navigation, Cambridge,Massachusetts, United States,2007:147-155.

[5]刘瀛翔，李垣陵，唐小妹,等.电离层对BOC调制信号的影响[J]. 宇航学报, 2012, 33(10): 1466-1471.

LIU Yingxiang, LI Yuanling,TANG Xiaomei, et al, Effect of ionosphere on BOC modulated signals[J]. Journal of Astronautics, 2012, 33(10): 1466-1471. (in Chinese)

[6]Misra P, Enge P K.全球定位系统—信号、测量与性能[M]. 罗鸣，曹冲，肖雄兵,等译. 北京: 电子工业出版社, 2006.

Misra P, Enge P K. Global positioning system signals,measurements,and performance[M].Translated by LUO Ming,CAO Chong,XIAO Xiongbing,et al. Beijing: Publishing House of Electronics Industry， 2006. (in Chinese)

[7]Kaplan E D, Hegarty C J. GPS原理与应用 [M]. 寇艳红,译. 2版. 北京：电子工业出版社, 2012.

Kaplan E D, Hegarty C J. Understanding GPS: principles and applications[M].Translated by KOU Yanhong. 2nd ed. Beijing: Publishing House of Electronics Industry， 2012. (in Chinese)

[8]Betz J, Capozza P, Fite J. System for direct acquisition of received signals: US, US7447259[P]. 2008-11-04.

[9]Liu Y X, Tang X M, Zhang K, et al. Dual sideband model for BOC modulated signals[C]// Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, United States, 2011: 2160-2166.

http://journal.nudt.edu.cn

Ionosphere dispersion effects simulation for high order BOC modulated signals

PANGJing,LIUYingxiang,TANGXiaomei,OUGang

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：The time delay and dispersion effects caused by the ionosphere need to be simulated in the navigation signal simulator. The higher order BOC modulation signal in the new generation of satellite navigation signals has a wider bandwidth than the traditional navigation signal. The simulation method of the traditional navigation signal can lead to the non-negligible modeling error of the ionosphere delay. An improved simulation method of BOC signal based on the bilateral model was presented, and was verified by simulation. The simulation results show that there is an error of meter in the ionosphere delay of the BOC (14, 2) signal, and the improved method can accurately simulate the effect of the ionosphere dispersion.

Key words：satellite navigation; BOC modulation; ionosphere effect; signal simulation

中图分类号：TN967.1

文献标志码：A

文章编号：1001-2486(2015)06-074-04

作者简介：庞晶(1978—)，女，山西新绛人，讲师，博士研究生，E-mail：pangjingnudt@126.com

基金项目：国家自然科学基金资助项目(61403413)

收稿日期：*2015-03-01

doi:10.11887/j.cn.201506015