记一次课本习题的“淘宝”历程

●张明远 何文魁 张 博 (陇西县第二中学 甘肃陇西 748100)

记一次课本习题的“淘宝”历程

●张明远 何文魁 张 博 (陇西县第二中学 甘肃陇西 748100)

教材中的例(习)题是经过专家精心构思、反复推敲后选定的，具有起点低、入口宽、视角广的特点，是高考复习之本，也是高考命题之源．深入研究例(习)题，揭示其深刻性，领悟其奥妙，对培养学生分析问题、解决问题的能力及抽象思维能力有着独特的功效．课堂教学中，教师在引导学生完成例(习)题后，要有意识地引导学生对问题全方位、广角度、多层次地进行引申、拓展，为学生提供教科书之外广阔的探究空间，有助于激发学生的学习动力，实现知识的“再创造”，使学生的数学思维提高到一个由例及类的档次，形成有效的“思维链”，达到“一题串一簇，一题联一线”的境地．如果经常这样做，学生头脑里就能喷发出探究的“火花”，思维就能得到真正地提升．下面笔者从一道课本习题到高考题的演变说起，例谈高考复习应从课本习题的后花园中“淘宝”，自觉挖掘课本习题的价值，传递课本习题承载的更多“能量”，追求课本习题的附加值．

1 问题呈现

问题1已知点A，B，C是抛物线y2=2px(其中p＞0)上的动点，且点A与点B关于x轴对称．直线AC，BC分别交x轴于点D，E，求证:DE被点O平分．

(人教A版教材选修4-4“极坐标与参数方程”第34页习题2．2第4题)

(人教A版教材选修4-4第34页习题2．2第2题)

2 问题探究

从而|OP|·|OQ|=a2(定值)．

到此问题解答已圆满结束，如果就题论题，缺乏对问题的类比迁移，无异于“登宝山而空返”(罗增儒语)．由于圆锥曲线具有“家族现象”，自然地思考这一结论对椭圆和双曲线是否也成立?在元认知的指引下，先类比迁移到椭圆中去探个究竟．

3 问题拓展

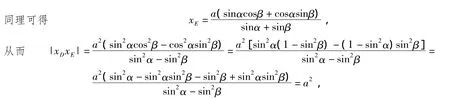
故|OD|·|OE|=a2(定值)．

拓展2已知点A，B，C是椭圆上的3个动点，且点A与点B关于x轴对称，直线AC，BC分别交y轴于点D和点E，探究点D与点E的纵坐标之间的关系．

仿拓展1，不难得到结论|OD|·|OE|=b2．

图3

回顾反思拓展1后，发现|OD|·|OE|=a2(定值)．其中a是|OD|，|OE|的等比中项，由|OD|·|OE|=a2为定值，联想到圆的切割线定理．如图3，过线段DE的中垂线上的一点G为圆心、GD为半径作⊙G，过点O引⊙G的切线，切点为P，则由圆的切割定理可知，|OD|·|OE|=|OP|2，则|OP|=a．设∠DOP=θ，由三角函数的定义不难得到点P的坐标为(acosα，asinθ)．OP是⊙G的切线，OED为⊙G的割线，由弦切角等于同弧所对的圆周角知，∠OPE=∠ODP，∠OEP=∠OPD．

进一步联想会发现，对于给定的⊙G，存在过原点的2条直线的2个定点满足∠OPE=∠ODP，∠OEP=∠OPD．

注:利用几何画板验证，双曲线也具有椭圆中这一类似的结论，并且|OP|·|OQ|的值为定值．感兴趣的读者可自行推导．

结语高三数学复习课应在教师深入理解教材和充分挖掘教材的前提下，适时、恰当地将结构良好(封闭性)的知识变为结构不良(开放性)的知识，引导学生积极主动参与问题探究的数学活动过程，这样才能丰富他们数学活动的经验，帮助他们提高“提出问题、分析问题、解决问题”的能力;这样才能在做数学的活动过程中深化对数学的理解，感悟数学的本质．唯有如此，才能让学生在数学课堂上走得更远，真正让数学课堂焕发出生命的活力．

综上所述，对任意 x1，x2∈R，x1≠x2，|f(x1) －f(x2)|＜1．

4 总结反思