一道课本习题引发的学与教的思考

●金晓群 (青田县第二中学 浙江青田 323900)

一道课本习题引发的学与教的思考

●金晓群 (青田县第二中学 浙江青田 323900)

课本习题是数学教材的重要组成部分，通常情况下，它比作业本、教辅资料等其他习题更为典型、精致．深入地理解课本习题的设计意图，并对某些习题进行自然、合理地挖掘开发，进而提升课堂教学的品质，应成为一线数学教师的不懈追求．笔者在组织浙教版《义务教育课程标准实验教科书·数学》九年级下册中2．2节“切线长定理”的课本习题(作业题A2)的教学时，课前对这道习题进行了有效的预设，课堂上又结合学生的实时表现，适当地对教学设计进行调整、改善，取得了不错的效果．可贵的是，一道普通的习题还引发了教师、学生对数学教与学问题的深层思考，现记录如下，供同行参考．

题目如图1，O为Rt△ABC直角边AC上的一点，以OC为半径的半圆与斜边AB相切于点D，交AC于点 E．已知 AB=5，AC=4，求 BD的长和⊙O的半径长．

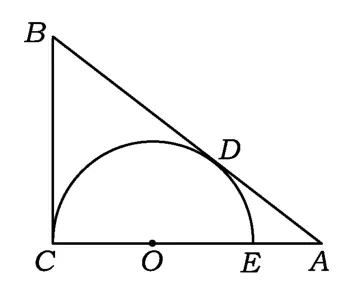
图1

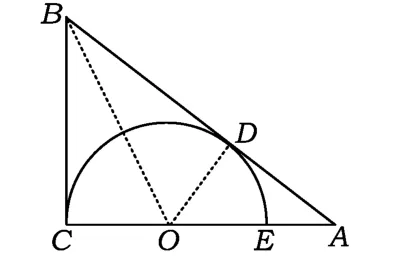
图2

1 学生解法展示

由勾股定理及切线长定理，容易求得BD=BC=3．在求⊙O的半径时，学生在充分思考后，展示了5种不同的解法(如图2):

展示了习题之后，笔者留给学生充分的时间进行求解与交流，坚持了“以学为中心、以学生为中心”的指导思想．出乎意料地，学生展示了5种解法，在课堂上完美地展现了“一题多解”的魅力．在这个环节中，由于学生们展示了不同的解法，借助表达、聆听、质疑、解释等方式，解题能力得到了锻炼，而且思维变得更加灵活、开阔．

巧合的是，这5种解法都运用到一种重要的数学思想——方程思想．方程思想在初中数学中是一种非常重要、应用十分广泛的数学思想，而要想让学生真实、深刻地体会数学思想，却并不容易．那么如何进行方程思想的渗透与落实呢?我们应该选择什么样的载体与着力点呢?“踏破铁鞋无觅处，得来全不费功夫”——该习题就是一个很好的选择．

当然，单单选择好范例，还不能算是成功的教学．为了使学生对方程思想有一个真切的认知，先对用方程解决问题的真实过程进行暴露是非常必要的．只有这样，学生才能较深刻地感受到运用方程解决问题的好处，进而体会到掌握方程思想的必要性，也为后续关于方程思想的深入学习、灵活运用打下基础．

2 解题之后，学生从“学”的角度进行思考

当然，仅仅是停留在学生们能用5种不同的方程解决问题，未免可惜．在笔者的指导与帮助下，学生们围绕着以下5个问题进行思考，并在课堂上展示了思考成果．

问题1这5种解法的共同特点是什么?

学生思考显而易见，这5种解法的共同特点是运用方程解决问题，具体地说，均是运用列方程的解法求线段的长．

问题2这5种解法所列的方程，其背后的根据分别是什么?

问题3这些“背后根据”为什么会提供方程?

学生思考这些方程背后的“根据”本身就是等式，而方程无非就是含有未知数的等式，因此这些“根据”为方程提供支持是非常自然的．

问题4列方程求线段长度的一般步骤是什么?

学生思考总体上说，可以用“设、表、列”这3个字来概括:第1步，假设相应的线段的长为某一未知数;第2步，用常数或含未知数的代数式来表示其他相关线段的长度;第3步，寻找到合适的等量关系，列出方程．

问题5本习题的求解对以后求解线段长度的问题有什么启示?

学生思考在求线段的长度时，可以思考以列方程求解的形式来进行．而在构建方程前，可以先从相似三角形的对应边成比例、勾股定理、面积公式、锐角三角函数、面积的和差关系、线段的和差等方面着手去寻找相应的等式．

由于本习题蕴含了浓厚的方程思想，因而上述过程中对学生“学”方面的思考是紧紧围绕这一数学思想展开的．一直以来，教师们都非常清楚数学思想在学习数学中的重要作用，平时在教学中也非常重视数学思想的渗透与落实．与数学的基本知识与基本技能相比，数学思想有“看不到、摸不着”的特点．因此在实际教学中，主要是从教师的角度，直白地、贴标签式地告知学生数学思想的名称，学生并没有发自内心地认同教师的讲评，只是表面地知其然，而不知前后的所以然，因此教学效果通常并不理想．

以上的第1个环节借助比较，使学生对运用方程解决问题有一个初步的了解;第2个环节通过寻找每个方程背后的理由，使学生对本题的求解掌握得更为深刻，也为今后在其他情形下运用方程解决问题指明大概方向;第3个环节进一步地探索这些根据和方程的本质联系，使学生感悟运用这些根据列方程的必然性;第4个环节借助对一般步骤的总结，让学生更扎实地掌握运用方程思想解决问题的常规手段;最后的环节通过把解本题拓展至更大范围、解更多题的猜想，让学生在未来的解题活动中能有所准备，能更顺利地求解其他题目．

在平常一些习题课的教学中，得出正确答案，教学也许就结束了，而这一次并不如此．在学生展示了不同解法的基础上，笔者引导学生对相关的具有规律化、本质化的内容进行总结和反思，尝试着从“怎么解”到“为什么这么解”层层递进，以求达到“解一题、会一类”的效果，对学生以后的数学学习无疑具有很大的益处．

3 习题教学之后，教师从“教”的角度进行思考

本习题的求解与讲评只是一堂新授课中的一个小小的片段，尽管这个习题难度并不大，但这个习题的求解及求解后对解法的总结，却简练而完整地体现了方程在求解线段长度时的魅力．在感叹之余，笔者围绕本习题的教学还有如下的思考:

思考1注重挖掘课本习题潜力

一堂新授课，要完成知识的落实与能力的提高，肯定是离不开题目的．在信息爆炸、题目泛滥的今天，如何选择习题是摆在一线教师面前的一个大问题．其实，课本中的习题是与课本内容完美配套的，而且编写的人员均是教材编写方面的专家，因此课本中的习题应该成为我们组织课堂练习的首选．更重要的是，教师要做课堂教学的有心人，能从普通的课堂习题中，挖掘出不一般的数学教育价值．当然，这种拓展要适时、合理、自然、有效．

思考2重视引导学生进行解决习题之后的归纳总结

数学的题目不计其数，要想从题海中解脱出来，必须注重解题策略的总结．因此，在学生解决某类问题之后，我们应该从更高的角度来引导学生思考“能不能解决类似的问题，能不能寻找到这类问题的共同属性，能不能用数学本质的眼光来看待问题”等问题．表面上看，在课堂上花在总结反思上的时间增多，完成的题目量减少，课堂效率可能会降低．但事实恰恰相反，只有注重这种反思，学生才能从根本上摆脱题目的束缚，更自由、更有效地学习数学知识，提升数学能力．在解题之后进行反思本应是一种必需的学习习惯，只不过由于教师或学生的浮躁，这种品质被边缘化了，变得可有可无．考虑学生的长远发展，教师必须要在这方面有所作为．

思考3注重提炼课本习题背后的数学思想解法

《新课标》提出:通过义务教育阶段的学习，学生能“获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验”，显然，这样的表述对数学思想的重要性给予了特别的强调．当然，数学思想作为数学的灵魂，它的重要性并不是课标制定的，而是学习数学、特别是解题的过程中自然体现的．数学习题无限多，为了使学生不被题海淹没，也为了保持学生的学习兴趣及未来可持续的学习动力，教师要有意识地对课本习题背后的数学思想进行提炼，并适时、合理地向学生渗透．

思考4习题中蕴含的数学思想的教学要“看得见、摸得着”

实际上，数学教师非常明白数学思想的重要意义，希望学生能马上掌握各种数学思想．但这一行动一旦操之过急，学生数学思想的学习往往被教师越俎代庖，被教师以贴标签的形式草草了之．由于不接地气，学生对数学思想的感觉是表面的、不踏实的、虚幻的，效果自然也不理想．其实数学思想的教学是急不得的，它就好像品德教育一样，需要学生慢慢地体会感悟，要有真实感知、扎实摸索、不断反思的过程．因此，数学思想的教学需要教师为学生寻找合适的时间和载体，搭建展示的平台，真实地展示学生在学习数学思想时或幼稚、或艰辛、或欢乐的足迹，尽量使数学思想解法的教学不一厢情愿、不故弄玄虚、不虚无缥缈，努力达到“看得见、摸得着”的效果．

作为从事一线教学的数学教师，我们应该做一个有心人，能从平平常常的教学素材中发现为我所用的精彩内容，并适时、适度地予以开发使用，为学生更有效地学习数学、更有兴趣地学习数学、更长远地学习数学，提供源源不断的支持．