基于模拟退火算法的兵力投送研究

2015-02-02王许来卢天鸣李宏伟

兵器装备工程学报 2015年12期

关键词：模拟退火

王许来，卢天鸣，李宏伟

(1.解放军理工大学野战工程学院，南京　210007； 2.南京理工大学机械工程学院，南京　210094)

基于模拟退火算法的兵力投送研究

王许来1，卢天鸣2，李宏伟1

(1.解放军理工大学野战工程学院，南京210007； 2.南京理工大学机械工程学院，南京210094)

摘要：陆军航空兵已经成为我陆军优先发展的兵种，兵力投送则是陆军航空兵重点发展之一，如何既能节省军费又能快速投送兵力至指定地域；运用模拟退火算法的技术对其路径进行优化从而获得最优解；最后通过实例验证了模拟退火算法在兵力投送中的应用价值，从结果可知，模拟退火算法对于兵力投送的最优路径选择有其明显的优势。

关键词：兵力投送；模拟退火；最优路径

本文引用格式：王许来，卢天鸣，李宏伟.基于模拟退火算法的兵力投送研究[J].四川兵工学报，2015(12):126-129.

Citation format:WANG Xu-lai, LU Tian-ming, LI Hong-wei.Research of Force Projection Based on Simulated Annealing Algorithm[J].Journal of Sichuan Ordnance,2015(12):126-129.

Research of Force Projection Based on Simulated Annealing Algorithm

WANG Xu-lai1, LU Tian-ming2, LI Hong-wei1

(1.Field Engineering College, PLA University of Science and Technology, Nanjing 210007, China;

2.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:Army aviation has become a prior development arm of services in our army, force projection is one of the critical points in army aviation. How fast can we deliver forces to the designated area and saves military expenditure? By using simulated annealing algorithm technology, we optimized force delivery path and then acquired the optimization result. The simulated annealing algorithm in military application value delivery was verified by an example. From the result we can see that simulated annealing algorithm has its own advantage to solve the problem about force projection.

Key words:force projection; simulated annealing; optimal routine

我国作为陆疆和海疆大国，陆上与14个国家接壤，除北方边界外，在其他所有方向上，我国都面临着非常恶劣的潜在安全威胁[1]。为适应新军事变革,陆军航空兵成为我国优先发展的军种[1]。陆军航空兵作为新兴的兵种，具有快速反应、灵敏多能的优点，对于应对突发事件和战场兵力投送有重要意义[2]。战场兵力投送是陆军航空兵的重要战略任务，对于兵力投送问题的研究，美军最早提出了兵力投送理论，开发了一系列配套的兵力投送模型，为兵力投送的研究和实践奠定了基础[3]。美军事交通管理司令部在1997年初基本建成了兵力投送模型，之后又有多个升级版本，其结构和功能都已趋健全[4]。法军在80年代初期也着手在陆军总部一级建成一个军交自动化系统，根据作战预案拟制部队输送计划[5]。

国内也开展了相应的研究，在兵力投送交通理论方面，军械工程学院张天平等研究了公路兵力投送中的定量风险分析模型[6],针对选择的运输路线进行了危险识别等。在军运物资投送方面，后勤工程学院樊荣等设计了油料投送模型，分析了最优投送方案[7]。兵力投送交通分析研究方面，郭树桂教授等所编写的《地理环境对陆上武器装备影响的建模研究》中建立了部队轮式车和履带式车辆的速度模型[8]。以上研究这对分析最短时间有着极大的应用价值，但是可以看出，以上研究仅针对公路兵力投送的问题，并没有谈及陆航部队的问题。由于直升机航程较短，载荷量小，在兵力投送过程具有其独特的限定条件，因此如何有效地利用有限的航程完成兵力投送任务，成为陆军航空兵部队亟待解决的问题。

兵力投送问题实质上就是最优路径问题，对于最优路径问题，模拟退火算法是一个比较高效的求解方式。因此，本文开展了基于模拟退火算法的陆航部队兵力投送最优路径研究。

1兵力投送问题的描述及数学模型

兵力投送是指一个国家各个战区为了遂行多样化军事行动将作战人员、物资、装备，向指定地区快速移动的行动，是一种战略战役范围内的兵力机动，具有规模大、距离远、速度快等特点，是保障军队快速反应、抢占先机的首要选择，也是保障我军在广阔空间完成多样化军事任务的有效支撑[9]。兵力投送可分为：从一点出发投送兵力至一个地点；从一点出发投送兵力至多个地点；从多点出发投送兵力至一个地点；从多点出发投送兵力至多个地点。第1种情况是最基础的情况，也是最简单的情况；第2种情况较为复杂，涉及到最优路径的选择；第3种情况是第一种情况的简单重复；第四种情况则是第二种情况的重复。因此，本文针对第二种情况进行研究。

如图1所示，节点1为兵力补给站，假定执行任务单位A的行军计划是将兵力投送至若干观察站，要求选择最优路径进行兵力投送，然后返回节点1。

图1　兵力分布

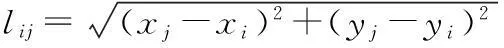
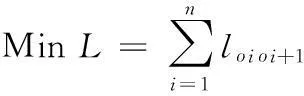
(1)

由于在兵力投送中可能会遇到敌防空火力打击的影响，有一定的风险，所以在计算最优路径时要考虑选择路径时的风险系数。假设敌侦察点的坐标为r0(x0,y0)，在作战区域任一点坐标为r(x,y)，被探测概率为Pd(x,y)。可以显见，被探测概率Pd与节点距敌侦察点距离l0有关，则

(2)

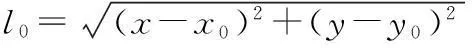
不同的危险系数在路径选择过程中，应当体现为不同的加权系数w(x,y)

(3)

其中：w∈[1,∞)。当被探测概率为0时，加权系数为1，即不加权；当被探测概率为1时，加权系数趋于无穷，即默认直升机被敌军击落。加权后的距离公式可定义为

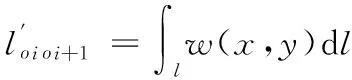
(4)

其中：l代表投送顺序相邻两点间的路径。则基于危险系数的最优路径模型为

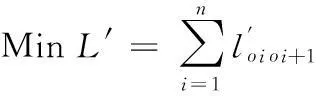
(5)

由于存在风险因素，所以兵力投送的最短路径将发生变化，较不考虑风险因素的路径而言，L′≥L。

在短时间间隔内，作战区域内的战场态势不随时间变化，作战区域内每一点距敌观察点的距离固定不变，则每一点的危险系数不变，加权后的距离可由式(4)得到，此时基于危险系数的最优路径模型退化为式(1)的最优路径模型。

在实际作战时，敌军会采用包括侦察机在内的多种手段进行侦察，这时就出现了敌军的移动侦察点，作战区域内每一点距敌观察点的距离是是时变的，相应的每一点的危险系数也在变化。式(2)改进为

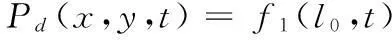
(6)

加权系数、节点距离以及最优路径模型也随之变化

(7)

(8)

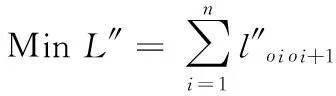
(9)

时变最优路径模型的求解需要考虑许多影响因素，包括敌移动侦察点出发时间、速度，我军直升机出发时间、速度等等，计算复杂，在这里不进行讨论。由于基于危险系数的最优路径模型可以退化为如式(1)的最优路径模型，因此，以最基础的式(1)所示的最优路径模型为例进行讨论。

2兵力投送模拟退火算法求解方法步骤

模拟退火算法(Simulated Annealing,SA)是基于Monte Carlo 迭代解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。SA 算法由某一较高初温开始,结合具有概率突跳特性的Metropolis抽样策略在解空间中随机寻找目标函数的全局最优解,伴随温度参数的不断下降重复抽样过程,最终得到问题的全局最优解。从算法结构知,新状态产生函数、新状态接受函数、退温函数、抽样稳定准则和退火结束准则( 简称三函数两准则)以及初始温度是直接影响算法优化结果的主要环节[10-11]。

兵力投送的SA算法的计算步骤描述如下：

1) 初始化。任意选取初始路径Oi∈S，S={O1,O2,…,On}是所有可能的路径组成的集合。给定初始温度T0、退温参数α,一般取α∈[0.80, 0.95]和终止温度Tf，令迭代指标k=0,Tk=T0。

2) 在第i次投送顺序中任意变换其中两个目标点的投送顺序，随机产生一个新路径Oj∈N(Oi)(N(Oi)表示Oi的领域)，计算路径增量ΔL=L(Oj)-L(Oi)。

4) 若达到热平衡 (内循环次数大于n(Tk))转5)，否则转2)。

5) 降低Tk，令Tk=Tk-1·α,k=k+1，若Tk

兵力投送的模拟退火算法流程如图2所示。

图2　模拟退火算法流程

3基于模拟退火算法的兵力投送求解

兵力补给站和观察站的坐标如表1所示。如图3所示为基于Matlab得到的兵力投送问题模拟退火算法求解结果。如图3(a)所示，利用模拟退火算法可以求得兵力投送的路径,由图3(b)可以看出当模拟退火算法在对10个节点的路径求解经过40步后趋于稳定，不再变化，说明在退火过程中温度已达到我们所期望的最低，也就是路径达到最优。可以看出，利用模拟退火算法求解兵力投送问题是有效可行的。