基于模拟遗传退火算法的RCPSP问题研究
2018-02-12赵卫东林双双
赵卫东 林双双


摘要:在资源有限项目调度问题中,针对可更新资源的单项目如何求得资源约束下的最短工期,提出了一种基于种群稳定度的遗传模拟退火算法。设计了一种满足任务前后约束的种群初始化方法,将种群进行交叉、变异产生新的种群后加入模拟退火算法,计算是否以新的种群替换当前新种群。提出了种群稳定度概念。为避免一般遗传算法的进化早熟现象,当种群稳定度超过给定的稳定度时应用模拟退火算法,通过多次试验设定种群稳定度。通过标准测试问题库中的数值验证表明,该算法能扩大解空间得到更优解,使收敛加快。
关键词:遗传算法;模拟退火;资源约束;种群稳定度
RCPSP Study Based on Simulated Annealing and Genetic Algorithm
ZHAO Wei dong, LIN Shuang shuang
(Shandong University of Science and Technology, College of Computer Scienceand Engineering,Qingdao 266590,China)
Abstract:In order to find the shortest duration for a single project with renewable resources under resource constraints, a genetic simulated annealing algorithm based on population stability is proposed. A population initialization method which satisfies the demand of precedence constraints is developed from this algorithm. After the new population is generated by crossing and mutating, the simulated annealing algorithm is added to calculate whether the current population is replaced by a new population. Meanwhile, the concept of population stability is put forward. In order to avoid the prematurity of general genetic algorithm, simulated annealing algorithm should be applied when the population stability exceeds the given stability which is determined by several experiments. Finally, the numerical results of PSPLIB show that this algorithm can expand the solution space, optimize the solution and accelerate the convergence.
Key Words:genetic algorithm; simulated annealing algorithm; resource constrained; population stability
0 引言
資源约束项目调度问题(Resource Constrained Project Scheduling Problem, RCPSP)是一类在满足既定的资源约束下,如何将项目中的各项任务进行合理调度以达到既定目标最优化的问题[1]。RCPSP问题是一个基本模型,最终目标是实现在最短时间内完成项目,属于“资源有限-工期最短”问题。在资源约束的同时,项目中的各项活动也有优先顺序约束,因此该问题也属于组合优化问题。工期最短化具有实际意义,在数学上RCPSP问题几乎都属于NP-hard问题[2],其研究方法一直在不断改进。分支定界法[3 4]、动态规划[5]等精确算法可在理论上取得最优解,但在实际应用中因为计算时间长和计算方法多而显得力不从心。基于优先规则的启发式方法是解决大规模问题的重要方法之一[6]。文献[7]提出在分层遗传算法中融入模拟退火思想能够避免种群过早收敛,同时能克服遗传算法局部寻优能力较差的缺陷。文献[8]提出基于磁石的交叉算子算法,能保证在相邻的部分两点交叉基因来自同一母体,与其它工序相比其性能较好。对于简单的可更新多资源及活动繁多的单项目优化研究不多,而在现代工厂的离散制造加工流程中单项目最短工期研究有一定的现实意义。因此本文在遗传算法后期设计一种能满足优先顺序关系约束的初始化种群,以有序的次序交叉法保证每一代个体的正确性和有效性,解决了可更新多资源约束下的单项目工期最短问题。实验证明本文算法允许以一定的概率接受较差解,可增加种群多样性,摆脱局部最优解,使收敛加快。
1 问题定义
资源受限的项目调度(RCPSP)问题[9]是用元组(A,D,E,R,B,W)表示的组合优化问题。
构成项目的活动由集合 A={a 0,…,a n+1}确定。a 0代表调度计划表的第一个活动,a n+1代表调度计划表的最后一个活动,二者是虚活动。为了绘图方便,引入一种特殊的活动,既不消耗时间也不消耗资源,仅仅表示工序的优先次序,称为虚活动。虚活动的工期和资源使用量都是0,实际参与活动集合是A′={a 1,…,a n}。
D是每个活动完成所需的时间集合,D={d 0,d 1,d 2,…,d i,…,d n,d n+1,0≤i≤n},d i是活动a i完成所需的时间,因此d 0=0,d n+1=0。
集合E给出了项目的优先顺序关系集合。如果(a i,a j)∈E,意味着活动a i必须先于活动a j发生。
可更新资源集合为R={r 1,…,r q},表示有r 1,r 2,…,r q共q种可更新资源。可更新资源的可用量在项目的每一时间段内都有约束,但消耗之后可在下一阶段更新。资源的可用性由B={b 1,…b k…,b q,1≤k≤q}表示,b k表示在任何时刻所有活动消耗资源r k的最大总量。活动对于资源的需求量用W表示。w ik表示执行活动a i的单位时间内消耗的资源r k的数量。单个工作日内所有作业对某一资源的需求量之和不得大于该种资源的供给上限,见式(1) :
用s i表示活动a i的开始时间,c i表示活动a i的结束时间,因此,c i=s i+d i,s 0=0,同时有s j≥c i,(a i,a j)∈E。如果设计的某个活动开始时间不满足这个约束,则需要将开始时间延后一天继续判断,直到满足这个约束为止,见式(2)。
“资源约束,工期最短”的RCPSP问题求最短工期的目标函数见式(3)。
2 算法设计
2.1 算法介绍
遗传算法(Genetic Algorithm,GA)由密歇根大学的Holland教授[10]于1975年提出,是借鉴自然界生物进化现象发展而来的。该算法将问题可能的解随机生成初始化种群,设定适应度函数(目标函数),将种群中的个体进行交叉(crossover)和变异(mutation)操作,根据适应度的值决定下一代种群的个体,循环操作直至达到终止条件。遗传算法擅长解决全局最优化问题,但是解决大规模计算量问题时容易陷入“早熟”[11 12]。而由Kirkpatrick等在1983年所发明的模拟退火算法,其最大特点是易于实现、运行效率高,而且允许以一定的概率接收差解,可有效解决遗传算法容易陷入局部最优解问题。同时遗传算法[13]具有很强的全局搜索能力,弥补了模拟退火对于解空间覆盖不足的缺陷,二者结合取长补短,可更有效地解决问题。
遗传和模拟退火算法结合仍有需要改进的地方。遗传算法每一代的种群都是随机生成的,最终遗传结果受初始种群影响较大,可设计一种符合资源约束的初始化种群生成方法,以保证进化一开始就是合格的个体[14 15]。遺传算法[16]对训练参数的依赖性较大,对参数的设定大部分依靠经验,并没有利用进化网络的反馈信息,故搜索速度较慢。增加种群稳定度概念,根据实验计算出合理的种群稳定度。当种群稳定度超过给定的稳定度值时,应用模拟退火算法,以新的种群替换当前种群[17]。
2.2 遗传算法实现
采用活动列表方式进行染色体编码,编码个体为 A j,0≤j≤n+1,表示项目中共有n+1个活动,每个活动(基因)可在满足活动的优先顺序关系约束下进行变动,这也是交叉变异操作的根据。
目标函数F(x)是满足资源约束时完成给定活动的最小时间。编码时仅考虑了活动的优先顺序关系约束。为了避免在算法进行中有不满足资源约束的非法个体参与[18],在种群初始化以及交叉变异等遗传算子操作时都要考虑资源约束。因此,这里的适应度函数f(x)直接取目标函数的倒数,即f(x)=1/F(x)。
初始化过程之前,先设定集合P=[p 1,p 2,…p i…,p j],1≤i≤j是活动的后继关系数组,p i是活动a i的后继关系约束数组,该数组可由优先关系集合E求得。假设E中共有4对关于a i的优先关系,分别是(a i,a j)、(a i,a z)、(a i,a w)和(a k,a i),由于活动a k是先于a i发生的,所以a i的后继活动有a j、a w和a z,所以pi=(a j,a w,a z)。种群初始化过程:假设某工程共有j个活动,给定两个有序集合A 1和A 2,A 1是所有活动的集合,A 2是空集合:① 从集合A 1中随机取出一个活动;② 如果活动a i是第一个取出的活动就直接放入A 2中,返回第①步,同时将a i从A 1中删除,如果不是则进行③步,当取出的作业为最后一个时转向步骤④;③ 判断p iA 2是否成立,如果成立,由于p i是a i的后继关系集合,说明a i的后继关系集合中的某个元素在A 2当前的活动集合中存在,因此将a i放在A 2中集合的最前方,以保证满足优先顺序关系集合E,同时将a i从A 1中删除;如果不成立,则将a i放回A 2中不作其它操作,返回步骤①;④ 将最后的活动放入A 2中当前集合的最前方,返回A 2,结束。
种群初始化中,要判断p i是否包含于A 2以保证个体符合后继数组约束关系,从集合A 1随机取一个活动保证个体随机生成。 遗传算子设计如下:
(1)选用经典的轮盘赌选择法,同时采用精英保留策略,将最优个体直接替代后代中最差的个体,保证最优个体最大程度得以保留,加快收敛速度。
(2)根据文献的次序交叉法思想,提出一种适用于RCPSP问题的交叉算法——有序的次序交叉算法(Orderly Cross Method)。取两个父代个体,随机选择两个交叉的点 x 1和x 2 ,父代一中两点之间的部分按照对应父代二两点之间的部分顺序放入子代一中,两点之外的部分不变,直接放入子代中,再采用相同方法产生子代二。由于子代跟父代相比变化的部分顺序依照另一父代,父代完全满足工序的紧前关系约束,因此产生的子代不会产生非法个体。需要指出的是,该方法在个体工序数较少时基因变化数目不多,类似于个体变异,因此可应用于基因数比较多的个体。
例如:
父代一:1 3 2 7 8 6 5 4 9
父代二:1 7 8 5 6 3 2 4 9
随机取第2和第5个位置,则父代一中取出“3 2 7 8”,相应父代二的顺序为“7 8 3 2”,先将父代一剩余的部分放入子代一中,则此时子代一为“1 x x x x 6 5 4 9”,取出的部分再按照父代二中的顺序替代子代中“xxx”部分,则生成的子代为:
子代一:1 7 8 3 2 6 5 4 9
子代二:1 7 8 6 5 3 2 4 9
(3)变异算子。本文遗传算子采用集中搜索策略,结合邻域技术寻求变异的最优后代。任取两个位置点,对两点之间的部分进行全排列。考虑到两点之间的个数较多,全排列产生的候选项过多会增大计算复杂度,因此此处规定两点之间的长度为4。全排列计算有可能产生不满足工序紧前约束的个体。将非法个体排除后,计算剩余个体适应度,选擇适应度值最高的作为新变异个体。如果全排列操作后除原本个体外全是非法个体,则重新选择两个位置点再次计算选择。考虑到如果多次选择位置点仍不能得到有效个体算法会陷入死循环,增加计算时间,因此规定重新选择10次后仍不能得到有效个体则重新以种群初始化方式新生成一个有效个体,替代原来需要变异的个体。
当算法达到最大遗传代数时算法终止,或者种群中个体不再发生变化时算法终止。
2.3 种群稳定度
在遗传算法后期,平均适应度对应的个体和最大适应度个体被选择进入下一代的概率趋于一致,容易使收敛停滞,为解决这一问题提出了种群稳定度(Population Stability,PS)概念[19]。种群稳定度(PS)指当前种群中个体适应度的离散程度,这里用方差记录。
决定算法能否得出一个较准确的结果,PS值的确定尤为重要。选取RCPSP标准测试问题库PSPLIB中J30数据集和J60数据集中各10组数据进行实验,利用上文给出的遗传算法进行计算,求出每一代的稳定度和目标值。通过多组数据多次计算可以得出,稳定度和目标值是负相关的。以j3019_5为例,稳定度和目标值两组数据拟合的2次函数结果见式(4)。
得到的相关系数矩阵见式(5)。
拟合的图像如图1所示,横坐标为稳定度,纵坐标为目标值。
从图1很容易看出,稳定度和目标值呈负相关,即稳定度越高目标值越低,效果越优。要想获得更优的目标值,也就是更短的工期,需要群体的稳定度更高,群体的离散程度更高,因此设定种群稳定度的指定值是种群最差的目标值所对应的稳定度的平均值。
2.4 模拟退火算法实现
仿照自然界物种灭绝的自然法则,当种群稳定度低于上节算出的平均值时,应用模拟退火操作判断是否以新的种群替换原来的种群进行算法迭代[20]。
加入模拟退火算法步骤:
(1)在满足条件的种群v 0邻域内随机选取一个可行解v i。
(2)随机生成[0,1]之间的双精度型小数p。
(3)判断由式(6)计算出的结果R(T)是否大于p,若大于则用v i替换v 0,反之不替换。
其中,f(v i)和f(v 0)分别为v i和v 0的种群最小目标值,T为进化代数,由此可见R(T)是随着T的增大而减小的,因此能使算法在进化前期更多地接受恶化解,在后期更多地接受优化解。
3 实验设计与结果分析
3.1 实验设计
PSGASA算法验证采用RCPSP标准测试问题库PSPLIB中的数据,选取j30、j60数据集,在每个数据集中随机选取10组数据。每组数据共享4种单模式资源,每个活动用到一种或多种资源且资源可再生,即可更新资源。每组数据中详细介绍了项目的活动与资源的需求匹配关系、资源类型及总量、活动资源需求量、活动的后继数组关系集合以及单个活动的计划工期等参数。
采用MATLAB语言编程。遗传算法开始的种群规模设定为50个个体,进化代数为100代,交叉率0.8,变异率0.1,j30数据集中个体数32个(包含第一个和最后一两个虚活动),j60数据集的个体数是62个。
3.2 结果分析
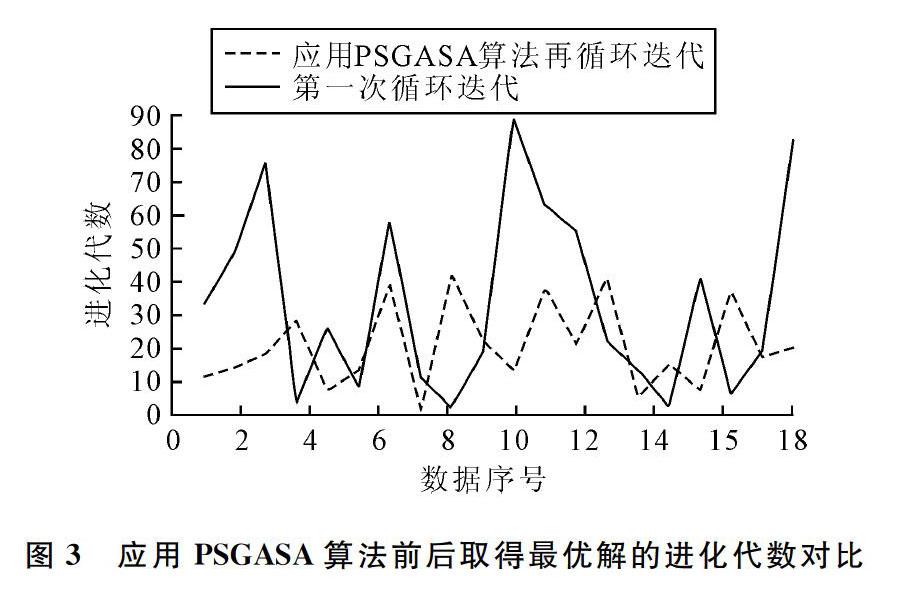
最终优化结果如表1所示。数据文件一栏是j30和j60中各自随机选取的10组数据,初始目标值是第一次循环迭代后计算出的目标值,最优目标值是在应用PSGASA算法后再次循环迭代计算出的目标值,可以看出大部分都得到了优化。j301_3的最佳调度方法如图2所示,其余数据由于篇幅所限不再列出。
图3给出了应用PSGASA算法前后取得最优解时的进化代数对比。结合表1和图3可以看出,在j30的10组数据中,有4组数据找到了更优解,4组数据持平, 3组解较差,但寻找到解的进化代数得以提前;在j60的10组数据中,有3组数据找到了更优解,6组数据持平, 1组解较差,持平的数据中寻找到解的进化代数得以提前且趋于稳定。由此可知,算法收敛性得到了加强,扩大了解空间,性能有所提高。
4 结语
PSGASA算法具有GA的全局搜索能力及SA的局部搜索能力,能使SA算法充分利用GA的全局信息,对全局解空间有详细了解[21]。通过建立满足资源和优先顺序约束的初始种群,提出种群稳定度概念。通过实验求得种群稳定度值,避免进化过度依赖初始参数。当种群达到一定的种群稳定度时,应用模拟退火算法判断是否以新的种群替换原来的种群,继续进行算法迭代,扩大解空间,找到更加准确的解。
通过实例验证,该改进算法能在全局空间中更准确地得到更优解。需要注意的是,PAGASA算法只是在相同进化代数中加快了速度,找到更优的解,与增大进化代数相比性能要差,但后者却需要更多的计算资源。此外,该算法只针对可更新资源,现实中有很多可更新资源与不可更新资源并存的项目,如何求单项目中两种资源类型并存的资源工期最短问题是下一步的研究重点。
参考文献:
[1] CHAKRABORTTY R K, SARKER R A, ESSAM D L. Multi mode resource constrained project scheduling under resource disruptions[J]. Computers & Chemical Engineering, 2016(88):13 29.
[2] DEB S, FONG S, TIAN Z, et al. Finding approximate solutions of NP hard optimization and tsp problems using elephant search algorithm[J]. Journal of Supercomputing, 2016, 72(10):1 33.
[3] CHEN C, ATAMTüRK A, OREN S S. A spatial branch and cut method for nonconvex qcqp with bounded complex variables[J]. Mathematical Programming, 2016(6):1 29.
[4] ERENGUC S S,AHN T,CONWAY D G.The resource con strained project scheduling problem with multiple crashable modes:an exact solution method[J].Naval Research Logistics,2001,48(2):107 127.
[5] HINDELANG T J,MUTH J F. A dynamic programming algorithm for decision CPM networks[J].Operations Research,1979,27(2):225 241.
[6] KOLISCH R.Efficent priority rules for the resource constrained project scheduling problem[J].Journal of Operations Management,1996,14(3):179 192.
[7] 李敬花,胡載萍,吕慧超,等.多资源约束下海工装备多项目调度优化[J].哈尔滨工程大学学报,2013,34(10):1214 1217.
[8] ZAMANI R. A competitive magnet based genetic algorithm for solving the resource constrained project scheduling problem[J]. European Journal of Operational Research ,2013,229(2):552 559.
[9] 方晨,王凌.资源约束项目调度研究综述[J].控制与决策,2010,25(5):641 650.
[10] BRUCKER P, DREXL A, M¨OHRING R. Resource constrained project scheduling: notation, classication, models, and methods[J]. European J of Operational Research, 1999, 112(1): 3 41.
[11] KOLISCH R.Efficent priority rules for the resource constrained project scheduling problem[J].Journal of Operations Management,1996,14(3):179 192.
[12] 何杰光,陈新度,陈新,等. 求解资源受限项目调度的动态多样性进化策略[J]. 计算机集成制造系统, 2015,21(8):2091 2093.
[13] LIU S X, CHEN D, WANG Y F.Memetic algorithm for multi mode resource constrained project scheduling problems[J].Journal of Systems Engineering and Electronics,2014,25(4):609 617.
[14] ZOULFAGHARI H,NEMATIAN J,MAHMOUDI N,et al.A new genetic algorithm for the RCPSP in large scale[J].International Journal of Applied Evolutionary Computation, 2013, 4 (2):29 40.
[15] DONG N, GE D D, FISCHER M,et al.A genetic algorithm based method for look ahead scheduling in the finishing phase of construction projects[J].Advanced Engineering Informatics,2012,26 (4):737 748.
[16] CHEN W N ,ZHANG J . Scheduling multi mode projects under uncertainty to optimize cash flows: a Monte Carlo ant colony system approach[J].Journal of Computer Science & Technology,2012,27(5):950 965.
[17] 梁亚澜,聂长海. 覆盖表生成的遗传算法配置参数优化[J].计算机学报,2012,35(7):1523 1526.
[18] ZHANG G H, GAO L, SHI Y.An effective genetic algorithm for the flexible job shop scheduling problem[J].Expert Systems with Applications,2011,38(4):3563 3573.
[19] 方晨,王凌.资源约束项目调度研究综述[J].控制與决策,2010,25(5):642 643.
[20] GONCALVES J F,MENDES J J M,RESENDE M G C.A genetic algorithm for the resource constrained multi project scheduling problem[J]. European Journal of Operational Research. 2008,189(3):1171 1190.
[21] FLESZAR K,HINDI K S. Solving the resource constrained project scheduling problem by a variable neighbourhood search[J]. European Journal of Operational Research,2003(2):402 413.
