浅谈高中数学函数定义域求法

金昌欢

(江西省新建区第一中学，江西 南昌　330100)

浅谈高中数学函数定义域求法

金昌欢

(江西省新建区第一中学，江西 南昌330100)

摘要：函数是高中数学的核心内容，贯穿在整个数学中。函数的三要素是定义域、值域以及对应法则。本文简明扼要的阐述了函数定义域的重要性，并对函数定义域的求法做出了详细的讲解。

关键词：高中数学；函数定义域求法

函数的定义域教学在函数教学中占据着重要地位。函数的定义域，是指函数自变量的取值范围。定义域、值域和对应法则是构成函数的三要素，其中定义域和值域起着决定性作用，定义域和对应法则，则是决定了函数的值域。

一、掌握函数定义域的方法

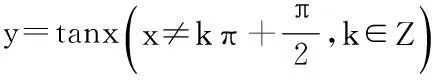
二、函数定义域的求法

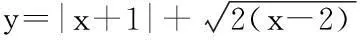
即函数值域[3,+∞]在解决分段函数的相关问题时，必须考虑端点的作用。图像法的有效利用体现了数学结合的基本思想。特别是在求函数值域方面，显得尤为重要。

(二)直接法。直接法，也被称之为观察法，对于普通函数的求解，首先要确定自变量的取值范围，了解y=f(x)的相关取值范围。通过的函数定义域，再结合相关的图像，正确判断函数的值域。当在求解函数的值域过程中遇到算术平方根时，首先考虑算术平方根的自身特性：非负性。有些复杂的函数在具体的解题过程中，首先进行仔细地观察，遇到可以直接看出值域的函数时，就不需要再继续解题。

1.配方法。配方法，主要通过求“二次函数”的值域。如F(x)=af2(x)+bf(x)+c的函数的值域问题，都可以使用配方法，但是在使用过程中，一定要注意x的取值是否存在范围的条件。求函数的值域，不但要重视对应关系的应用，更加要注意的是，定义域对值域的制约作用。配方法是解决数学函数的一种重要的思想方法。在求解函数的值域时，应该充分考虑配方法。当然，实际解题的过程中也要观察函数定义域的影响。

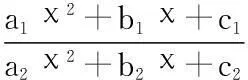
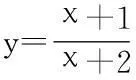
通过对该例题的分析，可以看出反函数解题法的优越性。但是，反函数与原函数的定义域和值域是互换的。这也是解决值域问题的一种解题技巧。除此之外，像如求导法等一些常用的方法对于解决函数值域问题也比较方便。

5.替换法。这种方法主要用一些其他的变量替换原函数的参量。通过这种替换可以使问题变得简单易懂，在很短的时间内就能解决值域问题。替换法主要是针对那些带有平方根或者含有分母的不等式。如果仅仅依靠常规的解决方法，运算量较大，整个的解题思路比较繁琐，最后还未必可以得到准确的答案。但是替换法引入的新变量在定义域方面与原函数的定义域相同，最终只是形式不同。

6.比例法。这种方法只是针对一部分的函数。当这类函数在求解值域方面遇到困难时，通过相关条件的转换，可以选用一些特殊的目标函数，然后快速地解出值域。

三、结束语

综上所述，解决数学函数的定义域方法多种多样。在求解函数定义域的过程中，同学们应该认真审题，从众多方法中，挑选出最快解决问题的方法。当然，这些解决方法还是不够的，只要自己熟练掌握函数定义域的规律，面对任何的函数问题，都能够灵活的解决定义域的问题。

参考文献：

[1]蒋明权.函数定义域求法分类例析[J].第二课堂(高中),2010,12:9-11.

[2]周荣.浅谈高中数学的函数基本性质的教学[J].数学学习与研究,2015,15:52.

中图分类号：G633.6

文献标识码：A

文章编号：1671-864X(2015)12-0267-01