小学数学“综合与实践”中学生思维能力的提升

◎福建省漳州市芗城实验小学 黄惠娇

小学数学“综合与实践”中学生思维能力的提升

◎福建省漳州市芗城实验小学 黄惠娇

“综合与实践”是以问题为载体，以学生自主参与为主的学习活动。在组织数学综合与实践活动中教师可以通过鼓励探究、尊重个性、开拓思路等提升学生深入思考、独立思考和灵活思考等思维能力。

综合与实践；思维能力；实践活动；提升

《义务教育小学数学课程标准（2011年版）》对“综合与实践”内容做了较大的修改，指出：“积累数学活动经验、培养学生应用意识和创新意识是数学课程的重要目标，应贯穿整个数学课程中。‘综合与实践’是实现这些目标的重要和有效的载体。”

“活动”是“综合与实践”的主要形式，在教学中，我们应通过让学生动手操作，互相合作，积极主动去探究数学，认识数学，并学会综合运用所学的知识去解决实际问题，从而有效提升学生的思维能力。下面结合数学综合与实践活动，谈谈对提升学生思维能力所做的一些探索。

一、鼓励探究，提升学生深入思考能力

学生深入思考的能力表现在：善于预见事物的发展进程，能从复杂的表面现象中抓住事物的规律和本质；能从不同角度思考问题、解决问题。数学综合与实践活动中，教师要精心设计教学环节，鼓励学生自主探究，在激活学生思维的深度和广度上下工夫，提升学生深入思考的能力。

1.层层递进，提升思维的深度

数学家华罗庚说过：“人们对数学早就产生了枯燥乏味，神秘难懂的印象，成因之一就是脱离实际。”生活中处处有数学，数学也离不开生活，教师应善于挖掘生活中的数学问题，把它们作为学生学习的宝贵资源，创设一个个有趣的生活情境，引导学生层层深入，在解决问题的过程中提升思维的深度。

例如，学生学习了长方体特征及表面积计算等相关知识后，笔者设计了一个综合实践活动——“包装中的学问”。对于五年级学生来说，他们虽然已经具备一定的商品包装的生活经验，但很少从节约的角度去关注，更谈不上从数学的角度去探究包装的学问。

教学中，教师引导学生从“包装一个盒子”到“包装两个相同的盒子”再到“包装四个相同的盒子”，又拓展到“生活中不同规格的长方体形状物品的包装”。以现实生活中的问题为背景，让学生在活动与交流之中一步一步深入研究，在自主探索中获取知识，提升思维，实现知识体系的自主建构。

这样，由浅入深，在平淡中显深刻，于细微处见精神，既突出实践，又综合应用所学知识。尊重并调动学生的已有经验、创造和展现自主学习的过程，把学生的思维逐步引向深入。

2.注重开放，提升思维的广度

生活中的事物存在着千丝万缕的联系，数学的开放性、多样性正是生活的反映。在综合实践活动中，我们应重视开放性教学。这不仅有利于学生潜能的发挥，有效地提升学生思维的广度，更是培养学生创新意识，提高创新能力的有效手段。

例如，学习了长方体正方体的体积、容积等相关知识后，笔者设计了一个综合与实践活动——“如何计算不规则图形的体积”。教师出示一块橡皮泥，激发学生：“我们已经学习了长方体、正方体的体积计算方法，那么像这样一块不规则的橡皮泥，你们有没有办法计算出它的体积呢？”

生1：我们可以把橡皮泥捏压成一个近似的长方体或正方体，再计算出它的体积。

师：通过把不规则的物体转化成长方体，就可以计算出它的体积了。如果要计算的是一块不规则石头的体积又该怎么办呢？

学生小组讨论，合作探究，总结得出计算石头体积的步骤和方法。

生2：可以拿一个盛有水的长方体容器，把石头浸没在水中，然后量出容器的长、宽以及水面上升前、后的高度，再计算出上升的水的体积就是石头的体积了。

学生经过动手操作，分工合作，积累操作和推理经验，取得数据，并计算出石头的体积。教师继续引导学生探究，还有没有其它的方法可以计算出石头的体积呢？学生经过积极思考，提出：“可以把长方体容器装满水，再把石头放进去，然后计算出溢出的水的体积也就是石头的体积了。”学生思维的闸门打开了......数学活动中要经常引导学生从不同的角度、方位寻找解决问题的途径，从而拓宽学生思维的广度。

二、以生为本，提升学生独立思考能力

由于每个学生的知识经验、生活背景、思维方式不一样，因此他们对问题的思考方式也各不相同，教师必须尊重学生的这种个性要求，以生为本，让学生养成独立思考的习惯，提升独立思考的能力。

1.尊重个性，训练独创思维

“多元智能理论”告诉我们，人具有的潜能是多种多样的，每个人都有属于自己的聪明才智。因此在教学中我们要改变那种传统的整齐划一的学习方式，充分尊重每个学生的不同学习方式，尊重他们的个性要求，激发他们积极主动富有个性地参与到学习之中，使他们的潜能得以充分地发挥。

例如，学习了“长方体和正方体表面积计算”后，笔者设计了一个综合实践活动——班级需要制作一个装图书的无盖长方体木箱（如图①），你能算出至少需要多大的木板吗？学生以小组为单位，自主、合作、探究计算方法。由于学生有了计算长方体表面积的知识基础，通过观察图形，多数学生已经能用三种常规的方法解答了。解法一：（6×5+6×3+5×3）×2-6×5；解法二：6×5+6×3×2+5×3×2；解法三：6×5+（6×3+5×3）×2。虽然这些方法都能计算出木箱的表面积，但学生的潜能还没有开掘出来，于是教师进一步激发学生：“同学们试着从不同的角度思考，还有别的方法吗？再想想！”学生的思维又启动了......一个学生通过积极思考，兴奋地说出了他的独特方法：我们可以把木箱的5个面拼成“十”字形（如图②），木板的面积就是大长方形面积减掉四块小正方形面积，即解法四：（高×2+长）×（高×2+宽）-高×高×4，也就是（3×2+6）×（3×2+5）-3×3×4。他的独创思维令老师和同学赞叹不已。受到他的启发，又有其他同学提出了不同的方法了。

生1：把纸盒拆成一个多边形，用（高×2+长）×宽，求出大长方形的面积，再用长×高×2求出两个小长方形的面积，再相加，即解法五：（高×2+长）×宽 +长×高×2，也就是（3×2+6）×5+6×3×2。（如图③）

生2：这种解法是横着看那个大长方形，如果竖着看还可以这样解答，即解法六：（高×2+宽）×长+宽×高×2，即（3×2+5）×6+5×3×2。（如图③）

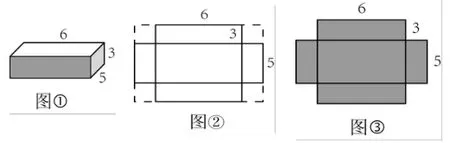
这种个性化的学习方式正是展开数学活动最有价值的教学资源。学生对待同样一个问题，不是人云亦云，而是能够积极地独立思考，寻找到多种有效的解决问题的方法。

2.引导反思，提升批判思维

反思应该成为学生一种重要的学习习惯，反思有利于学生知识的重新建构和审视自己的思维过程。教学中教师提供“错”的机会，让学生在认知矛盾中体验，并对自己的思维活动进行调整、校正，这样的训练有助于学生批判思维能力的提升。

例如，“购物中的学问”这一实践活动中，教师设计了这样一道题：“一个布娃娃40元，是一个皮球价钱的4倍，一个皮球多少钱？”有些学生凭着直觉不假思索，错解为：“40×4=160（元）”教师不动声色，将错就错，请学生再练一题：“爸爸今年40岁，是儿子年龄的4倍，儿子今年几岁？”果然有两位学生胸有成竹地解为：“40×4=160（岁）”。其他学生哈哈大笑，发出阵阵质疑声：“40岁的爸爸怎会有160岁的儿子？”“儿子怎会比爸爸大120岁？”……笔者适时抓住数量关系与学生进行讨论：①谁和谁在比？②谁大（多）谁小（少）？清楚这几点后，再引导学生反思，学生冷静下来之后，对自己的判断进行独立思考，对照错解细心感悟，重新选择适当的策略，及时纠错。教师要合理利用学生的错误资源，对学生在探索中产生的错误不必急于指正，相反，可以引导学生从不同角度检验推理过程的合理性，探索解决问题的新途径，提出修正方案，在反思中改错，提升学生思维批判能力。

三、开拓思路，提升学生灵活思考能力

灵活思考能力表现在学生能从不同角度，用多种方法解决问题，善于根据情况的变化迅速调整思维，概括迁移能力强，运用规律的自觉性高。

1.策略多样，提高思考灵活度

教师注重启发学生用立体的眼光去观察事物，从多角度全面而灵活地思考问题，探索新的解题途径。

例如，学习了乘法口诀后，笔者设计一个综合与实践活动——“创意插花”。花店里摆放着各种各样的鲜花。郁金香一枝8元，玫瑰一枝5元，康乃馨一枝6元，百合一枝7元，菊花一枝3元，剑兰一枝9元……小芳有30元要配一束花，怎样搭配？请你帮小芳配花。学生配花的方法灵活多样，有的从价钱上考虑，只要算够30元就行了，有多种方法，例如：6×5=30，7×3+9=30，8×3+3×2等。有的不仅考虑价钱，还要考虑搭配是否美观（颜色、枝数等）。学生还要考虑配花时出现钱有剩余或钱不够时如何处理等等问题。学生思维灵活，解决问题策略多样化。数学活动中教师要鼓励学生解决问题策略多样化，只有这样才能真正让学生灵活多变，活学知识、活用知识，提高学生思考灵活度。

2.迅速推理，提高思考敏捷度

有速度要求的分析推理练习是训练学生思维敏捷度的一个重要途径。教师引导学生从分析到综合，从综合到分析，全面而灵活地作“综合的分析”，提升思考的敏捷度。

例如，五年级下册“探索图形”这一综合与实践活动，目的是探索由小正方体拼成的大正方体的涂色规律，经历图形分类计数的思考过程。学生分别找出棱长2厘米、3厘米和4厘米的正方体的涂色情况，发现三面涂色的在正方体顶点的位置；两面涂色的在正方体棱上除去两端的位置；一面涂色的在正方体每个面除去周边一圈的位置；没有涂色的在正方体里面除去表面一层的位置。学生发现规律后，迅速迁移，分析推理，应用规律迅速找出棱长5厘米和6厘米的正方体的涂色情况，并进一步运用到更多的大正方体中。学生在探索规律的过程中，积累数学思维活动经验，从具体到抽象，从特殊到一般，用数学语言和模型正确表达发现的规律，拓展应用，迅速推理，提高了思维敏捷度。

总之，“综合与实践”强调数学知识的整体性、现实性和应用性，数学实践与综合应用是沟通数学知识内在联系的桥梁，有效开展数学综合与实践活动，能提升学生的思维能力。

陈志华）