一种新的精密星历内插方法

孙鹏，赵长胜，王仁

(江苏师范大学测绘学院，徐州 221116)



一种新的精密星历内插方法

孙鹏，赵长胜，王仁

(江苏师范大学测绘学院，徐州 221116)

摘要：GPS精密星历插值是精密单点定位的基础,本文将广义重心有理插值应用于GPS精密星历插值,同时验证了滑动广义重心有理插值算法在精密星历插值中的可行性,实验表明,滑动广义重心有理插值具有较好的稳定性及很高的内插精度,可以满足精密定位的需要。

关键词：精密星历;拉格朗日插值;重心拉格朗日插值;广义重心有理插值

0引言

获取GPS卫星的在轨位置是GPS定位的关键问题,获取卫星坐标有两种方式,一种是广播星历,一种是精密星历。广播星历通过导航电文的数据块Ⅱ直接发送给用户接收机,精度较低,不能满足精密定位需要。事后精密星历通常通过IGS网站下载,卫星坐标单位为km,精度已达2 cm,文件格式为sp3,每隔15 min给出一组星历数据。而通常GPS接收机的实际采样间隔为30 s、15 s甚至更密,因此我们需要对间隔15 min的精密星历进行内插或者拟合,以获取所需时刻的精密星历,目前最常用的方法是拉格朗日插值、Neville插值、切比雪夫多项式拟合等[1-3]。本文引入一种新的插值方法:广义重心有理插值,实验表明,该方法稳定性较好,精度高。

1拉格朗日插值与重心拉格朗日插值

设有n+1个插值节点,xj,j=0,1,…n,对应实数fj,j=0,1,2,…n,可构造n次插值多项式p,使p(xj)=fj,j=0,1…,n.则拉格朗日插值公式可以记为

(xj-xk),j=0,1,…n,

(1)

式中: lj(x)称为拉格朗日插值基函数;使用拉格朗日插值内插卫星位置时,x为需要的内插时刻; xj为插值节点的时刻; yj为插值节点三维坐标值。拉格朗日插值在节点较少时具有较高的插值精度,但计算量较大,且当插值节点增加时,容易出现振荡或跳跃现象,即龙格现象[4],因此,使用精密星历时通常采用低阶滑动拉格朗日插值,使待求历元位于插值节点中心区间以获得较高精度的插值结果[5-8]。

若定义重心权

wj=1/∏j≠k(xj-xk),j=0,1,…n.

(2)

则可得拉格朗日插值的改进形式:重心拉格朗日插值[9]。

(3)

重心拉格朗日插值分子分母都包含插值权wj,其插值权依赖于插值节点的分布,但对于等距节点插值,重心拉格朗日插值仍是病态的。文献[10]将重心拉格朗日插值用于精密星历插值,并得到一些有益结论。

2广义重心有理插值

重心有理插值可表示为

(4)

资助项目:国家自然科学基金(批准号:41174032); 江苏师范大学研究生科研创新计划重点项目(编号:2015YZD004)

联系人： 赵长胜 E-mail: zhaocs1957@126.com其形式与重心拉格朗日插值相似,区别在于插值权的选取。

现给定插值节点xi,i=0,1,…n及其对应的函数值fj,选择一个整数d,满足0≤d≤n,对每个i=0,1,…,n-d,令pi为点对(xi,fi),(xi+1,fi+1),…,(xi+d,fi+d)的次数至多为d的多项式,则构造有理函数插值为

(5)

式中:

(6)

将多项式pi(x)写成拉格朗日公式形式

(7)

将上式代入式(5),得

(8)

式中,

(9)

指标集Jk={i∈I:k-d≤i≤k}.根据常数1的拉格朗日插值公式有

(10)

可得:

(11)

将式(8)及式(11)代入式(5),得广义重心有理插值公式[11]为

(12)

式中,插值权wj由式(9)决定。

3验证与分析

选取由IGS提供的2015年4月4日精密星历数据(文件名为igs18386.sp3),提取卫星号为PG01的间隔为30min的卫星坐标(0:00-23:30),用广义重心有理插值(本文d取12)内插其余各已知点,将精密星历给出坐标作为真值,判断内插精度。内插结果如图1所示。

图1　三方向内插至15 min误差

内插结果显示,广义重心有理插值在最外侧出现了一定的波动情况,其中X方向在23:15处出现了1dm的误差,Y方向在0:15处出现了9cm的误差,Z方向在0:15处出现了接近1dm的误差。边缘处的结果用于精密单点定位是不够理想的,但1:00至22:00之间的插值精度可达1mm,而精密星历自身精度为厘米级,故这一时间段内的插值结果是可靠的。如果需要获取0:00-0:45以及22:45-24:00之间的插值结果,可以拼接前后两天的部分节点,即可获取当天任意时刻高精度插值结果。

也可以采用滑动插值的方式获取高精度插值结果。下面验证最佳插值节点数量以及d的最佳取值。以4月4日11:45为插值中心向两侧拓展10、12、14、16、18个间隔30min插值节点,并内插其间其余各已知历元,插值稳定性如图2所示。

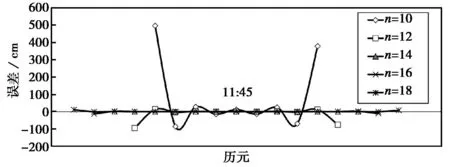
图2　不同节点数量端点突变

结果显示:采用10个节点的滑动广义重心有理插值是不可靠的,采用12、14、16、18个节点插值,插值中心区间是高度稳定的,且当增加节点数量时,边缘也相对稳定。

现使用上述数据不同节点数n内插11:45历元,求得插值误差detX,detY,detZ.如表1所示。

结果表明,采用滑动广义重心有理插值时,当取12个节点,d取10时插值精度可达毫米级,取14个节点,d=12或16个节点d=12或14时插值误差可达亚毫米,当增加节点数量时,插值结果趋于稳定,由于精密星历自身精度为厘米级,故采取滑动广义重心有理插值精度高,可靠性好,可以用于精密星历内插。

表1　不同节点数n内插11:45历元误差

4结束语

1) 使用广义重心有理插值内插精密星历,精度高,稳定性好。

2) 给出了滑动广义重心有理插值的最佳节点数以及d的可选取值,为实际应用提供了参考。

3) 插值权的确定依赖于d的取值,d的最佳取值有待进一步讨论。

参考文献

[1] 刘伟平,郝金明. 一种新的IGS精密星历插值算法[J]. 武汉大学学报·信息科学版,2011,36(11):1320-1323.

[2] 陈鹏,陈正阳,李骁. 一种新的GPS精密星历插值方法[J]. 大地测量与地球动力学,2009,29(2):111-114.

[3] 杨学锋,程鹏飞,方爱平,等.利用切比雪夫多项式拟合卫星轨道坐标的研究[J]. 测绘通报,2008(12):1-3.

[4] 吉长东,徐爱功,冯磊. GPS精密星历拟合与插值中龙格现象的处理方法[J]. 测绘科学,2011,36(6):169-171.

[5] 何玉晶,杨力. 基于拉格朗日插值方法的GPS IGS精密星历插值分析[J]. 测绘工程,2011(5):60-62，66.

[6] 雷雨,赵丹宁,高玉平. 基于滑动式Lagrange插值方法的GPS精密星历内插分析[J]. 测绘工程,2013,22(2):34-36.

[7] 宫厚诚,李全海. 基于IGS精密星历的卫星坐标和钟差插值[J]. 全球定位系统,2009(5):24-26,38.

[8] 吴伟,任超,王文杰,等. 基于滑动式算法的IGS精密星历内插与拟合精度[J]. 地理空间信息,2013，11(2):69-70.

[9] 王兆清,李淑萍,唐炳涛. 一维重心型插值:公式、算法和应用[J]. 山东建筑大学学报,2007,22(5):448-453.

[10]赵辉,张书毕,张秋昭,等. 基于质心拉格朗日插值的GPS轨道标准化方法[J]. 全球定位系统,2011,36(2):15-18.

[11]FLOATER M S, HORMANN K. Barycentric rational interpolation with no poles and high rates of approximations[J].Numberische Mathematik, 2007,107(2):315-331.

孙鹏(1991-),男,硕士生,主要研究方向为GNSS数据处理。

赵长胜(1957-),男,教授,研究方向为大地测量与测量数据处理。

王仁(1990-),男,硕士生,主要研究方向为GNSS数据处理。

A New Method for Precise Ephemeris Interpolation

SUN Peng,ZHAO Changsheng,WANG Ren

(SchoolofGeodesyandGeomatics,JiangSuNormalUniversity,Xuzhou221116,China)

Abstract:Precise Point Positioning(PPP) is based on GPS precise ephemeris interpolation. This article uses Generalized Barycentric Rational Interpolation for precise ephemeris interpolation, and verifies that Sliding Generalized Barycentric Rational Interpolation is also feasible. The experiment shows that, Generalized Barycentric Rational Interpolation is precise and highly stable and can meet the demands of PPP

Key words:Precise ephemeris; Lagrange interpolation; Barycentric Lagrange interpolation; Generalized Barycentric Rational Interpolation

作者简介

收稿日期：2015-07-27

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)06-0089-03

doi:10.13442/j.gnss.1008-9268.2015.06.020