区域对流层模型在GPS高精度基线测量中的应用

孟祥伍

(吉林省地矿测绘院,长春 130062)



区域对流层模型在GPS高精度基线测量中的应用

孟祥伍

(吉林省地矿测绘院,长春 130062)

摘要：提出利用CORS网络的观测数据,基于PPP方法和多面函数拟合建立区域对流层模型,并利用该模型对GPS基线测量结果进行对流层延迟改正，通过实际GPS观测数据计算对比发现,该方法能够显著提高GPS基线解算精度,优于传统对流层改正模型。

关键词：GPS基线;CORS;区域对流层模型;PPP

0引言

GPS信号穿过对流层时,由于大气的折射作用,使得GPS信号的传播路径和传播速度发生改变,因此产生GPS测量中的对流层延迟[1]。由于受气象条件、测站位置等不同因素的影响,对流层延迟在天顶方向的值大约在1.9～2.5 m左右,在卫星高度角5°左右时甚至达到20 m,成为GPS测量中的重要误差源之一[2]。大气中干性成分和水汽成分造成的延迟分别称为干延迟和湿延迟,其中干延迟可以利用经验模型精确计算得到,而湿延迟难以利用传统的经验模型获得较高精度的估值[3-4]。

常用的对流层模型主要用霍普菲尔德模型(Hopfiled)和萨斯塔莫宁模型(Saastamoinen)，然而由于对流层结构的复杂性和变化的快速性,对流层延迟受到大气环境、测站地理位置、季节变化等多种因素影响,传统的对流层模型难以满足目前GPS测量精度要求[5]。本文提出利用PPP方法,基于GPS实测数据估计GPS测量时段的天顶对流层延迟,并利用多面函数模型对区域对流层延迟进行拟合,获得测站的对流层延迟,进行高精度GPS解算[6]。

1区域对流层拟合模型

1.1PPP估计天顶对流层延迟

GPS单点定位中,线性化伪距观测方程为

(Vion)i-(Vtrop)i,

(1)

线性化载波相位观测方程为

λφi=-liVX-miVY-niVZ-cVtR-

(Vtrop)i+∑δi.

(2)

利用PPP方法估计对流层天顶延迟时,一般使用已知站点的观测值,这样可以消除坐标参数估计带来的未知数,同时将精密卫星钟差和精密星历代入观测方程[7]，利用双频观测值消除电离层误差的影响,则上述伪距和载波观测方程转化为

M(θi(i))-Pj(i)+εp,

(3)

M(θi(i))-λ·Nj(i)-

λ·Φi(i)+εp,

(4)

式中: j为卫星号; i为观测历元; c为真空中光速; δρzd(i)为对流层天顶方向延迟; M(θi(i))为投影函数; λ为GPS信号波长。根据以上观测方程,构建未知参数的状态方程,同时利用卡尔曼滤波等方法对参数进行解算,从而得到每个历元的对流层延迟改正值。

联系人： 孟祥伍E-mail:mxw25901294@163.com

1.2多面函数拟合模型

常用的对流层延迟拟合模型主要是二次或三次曲面模型,在估计对流层平面上的变化时只是建立了一个简单的多项式模型,无法真实的反映对流层的精细变化。

多面函数的基本思想为:任意一个光滑的曲面总是可以用一系列规则的数学曲面以任意精度逼近表示。多面函数可表示为

(5)

式中: Q(x,y,xi,yi)为核函数; αi为模型参数; m为结点个数或显著数据点个数，通常核函数为正双曲函数或倒双曲函数为

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+

σ2]1/2,

(6)

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+

σ2]-1/2,

(7)

式中: (xi,yi)为二次曲面的顶点; σ作为圆滑因子反映二次曲面在其顶点处的锐程度。利用PPP方法计算CORS网内多个基站的对流层延迟后,由于CORS基站较为密集,观测质量高,观测数据多,利用多面函数对对流层延迟进行拟合,能够很好地反应对流层在平面上的相关性，另外考虑到对流层延迟受到测站高程的影响,需要对模型进行优化,增加代表高程的拟合参数为

bh+c.

(8)

2GPS测量实例分析

为了验证该方法在GPS定位中的作用,选取一条长度约为2.4km的基线进行实际观测和解算。接收机采样频率为30s,共观测24h,每2h为一个时段,共划分为12个时段。为保证解算的精度和准确性,首先与IGS站进行联测,获得该站的精确地心坐标,然后固定该站点对GPS基线进行解算。解算过程中分别采用霍普菲尔德模型、萨斯塔莫宁模型、区域对流层模型进行对流层改正,计算基线N、E、U三个分量和基线长度L.由于无法确定该基线的真值,因此根据基线重复率判断基线测量的精度为

(9)

图1是三种基线解算方案的基线重复率的对比图。其中圆圈符号曲线为不加对流层改正模型的解算结果;星号曲线为hopfield模型对流层改正结果;正三角形曲线为通过区域对流层模型改正得到的基线解算结果。从图中可以看出,无对流层改正模型的基线解算结果与其余两种方案有较大偏差,并且不同时段基线解算结果变化较大,说明对流层延迟对基线精度影响较大，而hopfield模型改正结果与区域对流层模型改正结果相比,较为接近,但是不同时段的变化仍然比较大,区域对流层模型不同时段解算结果变化较小,基本在平均线周围,说明区域对流层模型对GPS基线对流层延迟改正精度较高。

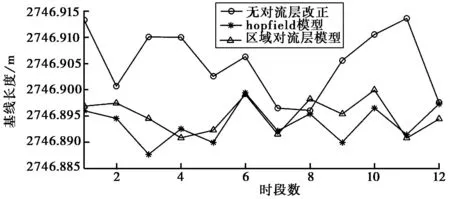
图1　三种方案基线重复率对比

表1示出了三种方案获得基线解算结果重复性精度统计结果。从表中可以看出,无对流层模型的基线解算质量相比于两种改正模型精度相差加大，而hopfield模型改正精度中,基线重复率R为0.000 43 m,不同时段基线结果标准差STD较大,为0.003 5 m.区域对流层模型改正后的基线解算结果相比于传统改正模型改正精度获得了显著提高,其中基线重复率R为0.000 32 m,不同时段基线结果标准差STD为0.002 8 m.说明该方法在实际中有应用前景。

表1　基线重复性精度统计/m

3结束语

对流层延迟对GPS测量精度影响较大,并且不能通过双频差分等手段完全消除，传统的对流层经验模型并不能满足高精度GPS测量的精度要求。本文提出利用当地CORS网络的观测数据建立对流层模型,对GPS观测结果进行对流层延迟改正。通过实际GPS基线测量项目的解算结果对比表明,区域对流层模型能够对GPS基线测量结果进行较好的改进,使得基线精度相比与传统对流层改正模型获得了显著提高。本文利用PPP方法计算对流层延迟需要IGS发布的事后精密星历、精密钟差等数据,不能做到实时建模,在实际工程应用中有一定的限制,利用预报星历、快速星历等数据进行该方法的计算精度需要进一步实验的验证。

参考文献

[1]熊永良, 黄丁发, 丁晓利,等. 基于多个GPS基准站的对流层延迟改正模型研究[J]. 工程勘察, 2005, (5):55-57.

[2]张笑凡, 何宏, 陈建峰. GPS技术中对流层延迟影响分析[J]. 测绘与空间地理信息, 2014, (2):187-188.

[3]张婷婷, 徐子乔, 董思学. GPS天顶对流层延迟计算方法研究[J]. 全球定位系统, 2013, 38(1):22-27.

[4]钱闯, 何畅勇, 刘晖. 基于球冠谐分析的区域精密对流层建模[J]. 测绘学报, 2014, 43(3):248-256.

[5]陈招华, 匡翠林, 蔡昌盛. 区域精密对流层延迟建模[J]. 武汉大学学报·信息科学版, 2011, 36(4):392-396.

[6]赵铁成, 韩曜旭. GPS定位系统中几种对流层模型的探讨[J]. 全球定位系统, 2011, 36(1):46-52.

[7]李凯锋, 欧阳永忠, 任来平,等. GPS精密单点定位中对流层延迟处理方法研究[J]. 测绘科学, 2009, 34(4):93-94.

孟祥伍(1972-),男,吉林长春人,工程师,主要从事测绘工程相关工作。

Application of Regional Tropospheric Model in GPS High

Precision Baseline Measurement

MENG Xiangwu

(JilinInstituteofGeologyandMineralResourcesSurveyingandMapping,

Changchun130062,China)

Abstract:The observation data of CORS network is put forward, and the model is built based on PPP method and multi surface function fitting. The model is used to correct the GPS baseline measurement. By comparing with the actual GPS data, it is found that the proposed method can significantly improve the accuracy of the baseline solution of GPS, and which has great advantages compared with the traditional troposphere correction model.

Key words:GPS baseline; CORS; regional tropospheric model; PPP

作者简介

收稿日期：2015-08-27

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)06-0049-03

doi:10.13442/j.gnss.1008-9268.2015.06.010