IGS轨道产品比较与分析

丁方

(同济大学测绘与地理信息学院,上海 200092)



IGS轨道产品比较与分析

丁方

(同济大学测绘与地理信息学院,上海 200092)

摘要：针对IGS不同分析中心卫星轨道产品之间的差异,利用IGS提供的最终精密星历和不同分析中心的精密星历,采用七参数转换模型计算坐标转换参数,消除产品间的系统性偏差,比较分析了不同产品的随机性误差。在此基础上,使用同一分析中心的卫星轨道和钟差产品,将IGS最终精密星历和钟差的精密单点定位(PPP)解作为参考值,比较了不同分析中心卫星轨道和钟差产品PPP解的点位误差。算例表明,虽然不同分析中心的卫星轨道和钟差产品存在差异,但是在采用同一分析中心的产品进行精密单点定位时,其定位结果的点位误差均小于1 cm,表明了同一分析中心的轨道和钟差产品具有一致性和自洽性。因此,用户可以配套的使用IGS不同分析中心的卫星轨道和钟差产品来代替IGS提供的最终产品,以得到高精度的定位结果。

关键词：轨道产品;七参数转换模型;随机误差;点位误差

0引言

高精度的卫星轨道是实现精密单点定位的关键。在精密单点定位中,采用高精度卫星轨道、钟差和单站观测数据就可以实现厘米级甚至毫米级定位精度[1]。IGS的七个分析中心(CODE、NRCan、GFZ、ESA、NGS、JPL、SIO)利用全球的GNSS观测数据,分别进行对应的数据处理与分析,并将处理结果发送给数据处理中心,然后综合分析中心将七个分析中心的结果取加权平均值,得到最终的IGS产品(其中包括卫星轨道产品和卫星钟差产品)[2]。

目前IGS所提供的精密星历的精度已优于5 cm,卫星钟差改正数误差约为0.2～0.3 ns[3-4].由于不同分析中心所解算的钟差结果相对于不同的参考钟,由此引入了因参考基准不同的误差,不同分析中心估计的卫星钟差的RMS的一致性[4]大约为0.1～0.2 ns或3～6 cm[5].此外,由于不同分析中心所采用的参考站分布、数据的不同以及所考虑的误差改正模型及所解算的参数并不完全一致,使得解算得到的GNSS卫星轨道产品存在系统性的偏差。因此消除不同分析中心的卫星轨道产品的系统性差异,分析不同卫星轨道产品的随机性误差,研究不同分析中心提供的卫星轨道和钟差产品的定位精度,才能更好地使用这些产品,指导用户实现高精度定位。

1数学模型

由于各个分析中心计算所得到的卫星轨道的参考框架不一致,首先要统一它们的参考框架。在七参数转换模型中,公共点之间的关系表示为[6]

(1)

联系人： 丁方 E-mail: 1335458@tongji.edu.cn

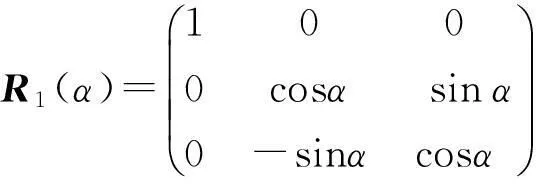
(2)

对式(2)不做近似处理,在构成误差方程进行平差解算时,对式(1)在参数近似值处泰勒展开进行线性化

(3)

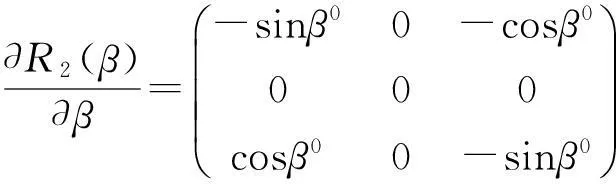
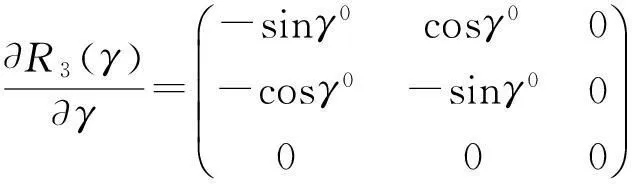
将每次计算出的参数改正值(δx0δy0δz0δμδαδβδγ)T加上上次计算时的参数近似值(x0y0z0μ0α0β0γ0)的和,作为本次参数近似值代入,第一次解算的近似值都设定为0,根据间接平差原理,

X=(δx0δy0δz0δμδαδβδγ)T

=(ATPA)-1(ATPl).

(4)

权阵P为单位阵,可以不断迭代解出新的参数改正值,直到解算出的δx0,δy0,δz0,δμ都小于10-5而且δα,δβ,δγ都小于10-7为止。

2数据分析

本文采用了IGS分析中心2014年7月1日至7月31日31天的精密星历与该时间段IGS最终的精密星历,分别计算每天不同分析中心卫星轨道与IGS最终卫星轨道的转换参数,将IGS最终卫星轨道作为参考值,消除了卫星轨道的系统性误差,研究了卫星轨道的随机性误差,在此基础上分析了不同分析中心对应轨道、钟差产品的一致性和自洽性。

2.1轨道比较

从图1可知,不同分析中心卫星轨道存在着一定的差异,其误差小于5cm;在经过坐标转换其后,卫星轨道的差异整体上有所减小,但仍然还存在着一定的系统性误差。例如SIO卫星轨道坐标转换前的平均RMS为3.134cm,转换后的平均RMS为2.753cm.从图2可知,在经过坐标转换后的卫星轨道残差除ESA外均表现出良好的随机性,它反映了产品之间的随机性误差,而ESA则还存在着一个明显的系统性误差。对于本文所采用的数据,系统性的误差在一定程度上影响了卫星轨道的精度,在定位时需要考虑它的影响。

图1　不同分析中心卫星轨道转换前后RMS

图2　不同分析中心卫星轨道坐标转换的残差

2.2PPP结果比较与分析

卫星轨道和钟差的精度都影响着精密单点定位的精度[2],因此本文采用2014年7月24日WTZR站的观测数据,使用同一分析中心的轨道和钟差产品进行精密单点定位,将IGS的定位结果作为参考值,计算其它分析中心的点位误差,其结果如表1所示。

表1　WTZR站采用同一分析中心的轨道和钟差产品的PPP结果

表1中,使用同一分析中心的卫星轨道和钟差产品进行精密单点定位时,其定位结果与IGS最终卫星轨道和钟差产品的定位结果的点位误差均小于1 cm;除CODE外,其余均在2～3 mm,达到了精密单点定位的精度,这反映了不同分析中心的产品具有一致性和自洽性。实际中,在用户进行精密单点定位时,由于IGS最终的轨道和钟差产品是七个分析中心的结果取加权平均值,其发布时间晚于这七个分析中心的产品发布时间,在一定情况下完全可以使用七个中心的卫星轨道和钟差产品来代替,也可以得到高精度的定位结果。

3结束语

本文研究了IGS不同分析中心卫星轨道产品存在参考框架的差异以及不同分析中心卫星轨道和钟差产品的定位精度、自洽性。采用七参数模型,计算转换参数,统一不同分析中心的卫星轨道的参考框架,比较了转换前后的RMS,得出参考框架的差异影响了卫星轨道的精度。在此基础上分析了不同分析中心的卫星轨道和钟差产品的定位精度。本文算例表明,虽然不同分析中心的卫星轨道和钟差产品存在差异,但当采用同一分析中心的产品进行精密单点定位时,其定位结果的点位误差均小于1 cm,表明了同一分析中心的轨道和钟差产品具有一致性和自洽性。在IGS最终卫星轨道和钟差产品未发布前,用户可以使用其他七个分析中心提供的卫星轨道和钟差产品,同样可以得到高精度的定位结果。

参考文献

[1] VAN BREE R J P, TIBERIUS C, HAUSCHILD A. Real time satellite clocks in single-frequency precise point positioning[C]//IONGNSS-2009, Savannah, Sept, 2009: 22-25.

[2] GAO Yang, CHEN Kongzhe. Performance analysis of precise point positioning using real-time orbit and clock products[J]. Journal of Global Positioning System, 2004, 3(1):95-100.

[3] 刘经南,叶世榕.GPS非差精密单点定位技术探讨[J].武汉大学学报·信息科学版,2002,27(3):234-240.

[4] 韩保民,欧吉坤.基于GPS非差观测值进行精密单点定位研究[J].武汉大学学报·信息科学版,2003,28(4):409-412.

[5] GAO Yang, JAMES F M. Single-point GPS positioning accuracy using precise GPS data[J]. The Australian Surveyor,1997,42(4):185-192.

[6] 潘国荣,周跃寅.两种坐标系转换计算方法的比较[J].大地测量与地球动力学,2011,31(3):58-62.

丁方(1991-),男,本科，主要研究方向为GNSS数据处理。

Comparison and Analysis of IGS Precise Orbit Products

DING Fang

(CollegeofSurveyingandmapping,TongjiUniversity,Shanghai200092,China)

Abstract:According to the different reference frame of satellite orbit products of IGS analysis centers, using final precise ephemeris and precise ephemeris respectively provided by IGS and its analysis centers, we adopt seven parameters transformation model to calculate the coordinate transformation parameters. Through seven parameters transformation, reference frames are unified. On this basis, using the same precise ephemeris and clock error products, taking precise point positioning (PPP) results of IGS final products as the reference, we analyze the positional error of different analysis centers’ products. Results show that, although there are some differences between the seven analysis centers, their positional errors are less than 1 cm. So products of the same analysis centers have consistency and self-consistency. Therefore, in certain cases users can take the products of the same analysis center to replace IGS final products. In this way, high precision positioning results can also be obtained.

Key words:Orbit products; seven parameters transformation model; random error; positional error

作者简介

收稿日期：2015-06-23

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)06-0079-04

doi:10.13442/j.gnss.1008-9268.2015.06.017