七模类Lorenz系统的界估计及计算机仿真

徐鸿鹏，王记昌

（河南工业职业技术学院 河南 南阳 473000）

1963年美国科学院院士E.N.Lorenz在研究大气对流时，首次给出了一个简单的三维自治系统，即著名的Lorenz系统[1]，采用的办法就是对Navier-Stokes方程和热传导方程进行Fourier级数展开进行截取前三项所得。以后，又有其他学者进行有限项截断，得到不同模数的非线性微分方程组[2-4]。混沌吸引子是相空间中的一个点集，随着运动时间的增加，所有轨线都趋向于它。这些混沌系统的全局吸引子的存在性和部分动力学行为已经被许多研究者所认识和研究。除了Lorenz系统族[5]之外，也存在其他混沌系统[6]，这些新混沌系统的提出和研究为混沌系统甚至混沌理论的应用提供了一定的理论基础和参考价值。文献[7]研究了Navier-Stokes方程的七模截断的全局吸引子的存在性，并给出了部分数值模拟图像，本文进一步考虑该系统，通过理论和数值方法给出了系统的相图、Poincare映射图、分岔图等揭示系统的复杂动力学行为，并构造出广义李雅普诺夫函数给出了新的全局指数吸引集的估计表达式，并给出理论计算和实际数值计算的结果比较，表明了本文方法的正确性。

1 数学模型及其主要结果

王贺元等研究的一个七模Lorenz混沌系统的方程为[7]:

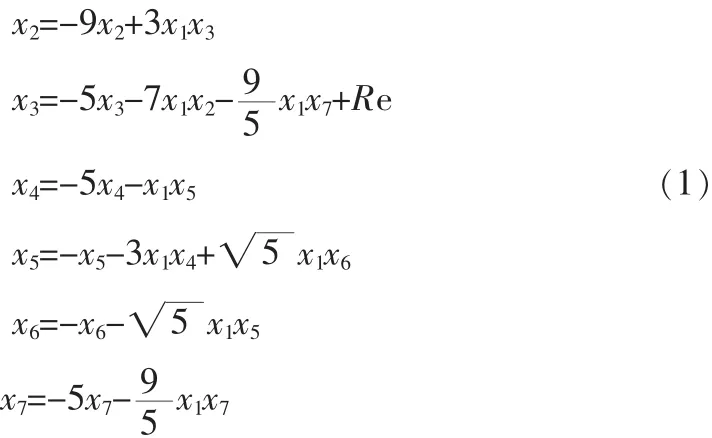
其中（x1，x2，x3，x4，x5，x6，x7）∈R7为状态变量，R e 为系统实参数。

系统（1）在坐标变换下（x1，x2，x3，-x4，-x5，-x6，x7）保持不变，说明系统具有该变化下的对称性。根据刘维尔定理，由于系统的平均散度所以系统属于耗散系统，并以指数e-28t收缩，说明系统存在吸引子。当R e=100时，初值取（1，1，1，1，1，1，1），系统（1）的轨线的吸引子相图如图1所示。

随着参数R e的变化，系统表现出稳定到平衡点、极限环 （周期轨或拟周期轨）和混沌吸引子等不同的非线性行为，即出现Hopf分叉和混沌现象。下面通过数值模拟给出不同于典型混沌吸引子的复杂周期轨的吸引子相图以验证图4中的结论，此时R e=200。并结合Poincare映射图来进一步加以说明，Poincare映射截面上有一些具有分形结构的密集点，说明系统是混沌状态，截面上只有几个离散的点，说明系统处于周期状态或拟周期状态。这与图3和图5的结论是吻合的。

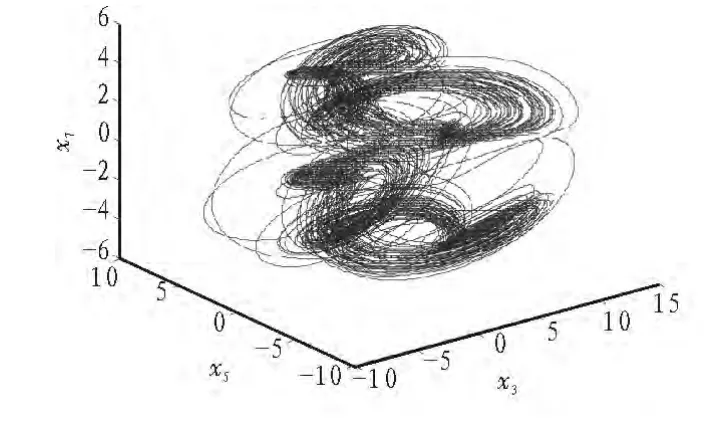
图1 系统（1）的轨线相图Fig.1 Phase portrait of system （1）

图2 系统（1）的分岔图Fig.2 Bifurcation diagram of system （1）

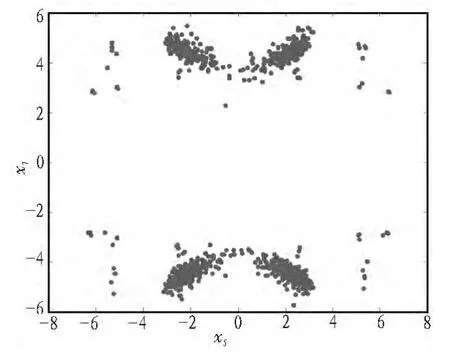
图3 Poincare映射图Fig.3 Poincare mapping diagram

图4 系统（1）的复杂周期轨Fig.4 Complex periodic orbit of system （1）

2 系统的界估计和数值模拟

下面给出系统的界估计和最终有界集的结论。

图5 系统（1）的Poincare映射图Fig.5 Poincare mapping diagram of system （1）

对V沿系统（1）的轨线对时间求导有，

注1：本文给出的结论比文献[7]的范围更小，为了便于比较，采用文献[7]的符号记法，在文献[7]中的结论

注2：该定理不仅给出了系统解的最终界估计式，而且给出了系统（1）的轨线从吸引集外进入吸引集的速率估计表达式。

当参数R e=100时，系统（1）的最终界估计表达式为，Ω=数值模拟如图15所示。

图6 混沌吸引子的最终界Fig.6 Ultimate bound of chaotic attractor

3 结 论

本文研究了参数Re变化时系统（1）的部分动力学行为和全局指数吸引集，并且给出了相应的计算机仿真[9]。由于该系统具有丰富的动力学行为，可以为信息加密技术提供良好的信号源，因此其混沌机理的研究以及电子振荡电路的实现是我们下一步研究的重点任务。

[1]Lorenz E N.Deterministic non-periods ows[J].J.Atoms.Sci.1963，20（2）:130-141.

[2]Franceschini V，Tebaldi C.A seven-modes truncation of the plane incompressible Navier-Stokes equations[J].Journal of Statistical Physics，1981，25（3）:397-417.

[3]Boldrighini C，Franceschini V.A five-dimensional truncation of the plane incompressible Navier-Stokes equations[J].Communications in Mathematical Physics，1979，64（2）:159-170.

[4]Franceschini V，Zanasi R.Three-dimensional Navier-Stokes equations truncated on a torus[J].Nonlinearity，1992，4（3）:189-209.

[5]尹社会，张勇，张付臣，等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师大学报（自然科学版），2014，46（1）:42-47.YIN She-hui，ZHANG Yong，ZHANG Fu-chen，et al.Dynamical behavior for the forced Lorenz system based on the Lorenz map and simulation[J].Journal of Northeast Normal University（Natural Science Edition），2014，46（1）:42-47.

[6]尹社会，张勇，徐鹏飞.一个三维混沌系统的动力学行为及反馈同步[J].江西科学，2013，31（6）:717-721.YIN She-hui，ZHANG Yong，XU Peng-fei.Dynamical analysis and feedback synchronization of a Three-dimensional Chaotic System[J].Jiangxi Science，2013，31（6）:717-721.

[7]WANG He-yuan，CUI Yan，HUANG Min.A new sevenmodes truncation of the plane incompressible Navier-Stokes equations[J].Chinese Quarterly Journal of Mathematics，2012，27（1）:11-17.

[8]Damei Li，Jun-an Lu，Xiaoqun Wu，et al.Estimating the bounds for the Lorenz family of chaotic systems[J].Chaos，Solutiona and Fractals，2005，23（2）:529-534.

[9]尤裕荣，袁洪滨，王春民，等.PWM高速开关阀动态调节特性仿真研究[J].火箭推进，2012（5）：24-29.YOU Yu-rong，YUAN Hong-bin，WANG Chun-min，et al.Simulation of dynamic regulating characteristics of PWM high-speed on-off valve[J].Journal of Rocket Propulsion，2012（5）:24-29.