全等三角形考题精选

朱海峰

1. （2015·江苏泰州）如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（ ）.

A. 1对 B. 2对

C. 3对 D. 4对

2. （2015·浙江绍兴）如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线.此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是（ ）.

A. SAS B. ASA

C. AAS D. SSS

3. （2015·江西省）如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB.则图中有_______对全等三角形.

4. （2015·湖南娄底）已知AB=BC，要使△ABD≌△CBD，还需要加一个条件，你添加的条件是_______.（只需写一个，不添加辅助线）

5. （2015·湖南永州）如下图，在△ABC中，己知∠1=∠2，BE=CD，AB=5，AE=2，则CE=________.

6. （2015·福建福州）如图，∠1=∠2，∠3=∠4，求证：AC=AD.

7. （2015·四川宜宾）如图，AC=DC，BC=EC，∠ACD=∠BCE.求证：∠A=∠D.

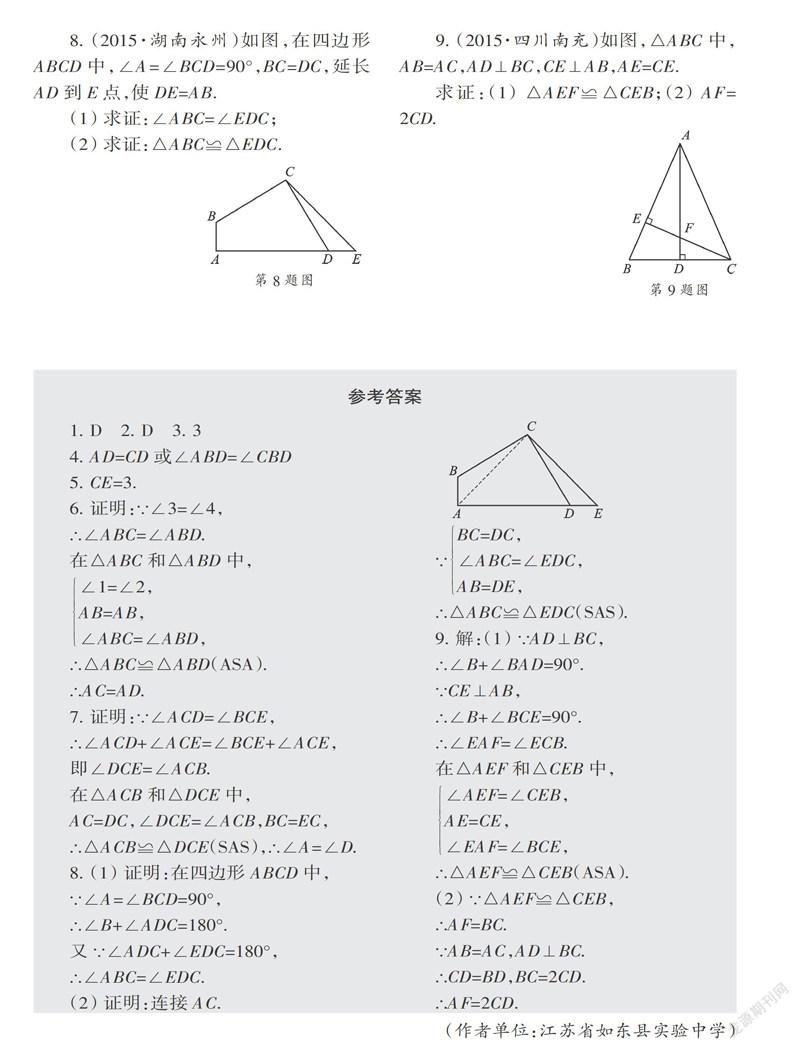
8. （2015·湖南永州）如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC，延长AD到E点，使DE=AB.

（1） 求证：∠ABC=∠EDC；

（2） 求证：△ABC≌△EDC.

9. （2015·四川南充）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE.

求证：（1） △AEF≌△CEB；（2） AF=2CD.

参考答案

1. D 2. D 3. 3

4. AD=CD或∠ABD=∠CBD

5. CE=3.

6. 证明：∵∠3=∠4，

∴∠ABC=∠ABD.

在△ABC和△ABD中，

∠1=∠2，

AB=AB，

∠ABC=∠ABD，

∴△ABC≌△ABD（ASA）.

∴AC=AD.

7. 证明：∵∠ACD=∠BCE，

∴∠ACD+∠ACE=∠BCE+∠ACE，

即∠DCE=∠ACB.

在△ACB和△DCE中，

AC=DC，∠DCE=∠ACB，BC=EC，

∴△ACB≌△DCE（SAS），∴∠A=∠D.

8. （1） 证明：在四边形ABCD中，

∵∠A=∠BCD=90°，

∴∠B+∠ADC=180°.

又∵∠ADC+∠EDC=180°，

∴∠ABC=∠EDC.

（2） 证明：连接AC.

∵BC=DC，

∠ABC=∠EDC，

AB=DE，

∴△ABC≌△EDC（SAS）.

9. 解：（1） ∵AD⊥BC，

∴∠B+∠BAD=90°.

∵CE⊥AB，

∴∠B+∠BCE=90°.

∴∠EAF=∠ECB.

在△AEF和△CEB中，

∠AEF=∠CEB，

AE=CE，

∠EAF=∠BCE，

∴△AEF≌△CEB（ASA）.

（2） ∵△AEF≌△CEB，

∴AF=BC.

∵AB=AC，AD⊥BC.

∴CD=BD，BC=2CD.

∴AF=2CD.