“北极航道”开通与中国及其受影响区域的贸易增长潜力分析

李珍 胡麦秀

(上海海洋大学,上海201306)

0 引言

近30多年的科学观测表明,北极海冰覆盖范围呈加速递减趋势,海冰厚度也明显变薄,“北极航道”商业通航指日可待。据统计,从2009年德国两艘货船试探性商业航行开始至2013年底,已有包括中远“永盛轮”在内的157艘船只经北极“东北航道”,运送货物达355.1万吨[1]。一旦“北极航道”开通并投入商业运行,其带来的航道利益将是非常可观的。

中国已成为世界第一贸易大国,其中,欧盟和美国是中国最主要的两大贸易伙伴。中欧、中美之间贸易量的90%需通过海洋运输来完成,并且都是经传统的苏伊士运河或巴拿马运河航线,然而这些航线的通航能力目前已经达到饱和,拥堵现象十分严重。“北极航道”的开通将使中国到欧洲或北美之间的海运里程缩短10%—55%,节省可观的运输成本或贸易成本。贸易成本的降低不仅会对中欧、中美之间的贸易潜力产生影响,而且也会使中国受“北极航道”影响的沿海地区的贸易增长潜力发生较大变化。

国际上有关“北极航道”相关问题的研究起步较早,不论在技术层面还是在软科学层面都积累了大量实践和理论研究基础。国内对于“北极航道”的科学考察和研究相对较晚。从中国开始第一次“北极航道”的科学考察以来,至今共进行了五次科学考察,分别是1999年、2003年、2008年、2010年和2012年。相关研究人员获取了大量的第一手观测资料和样品,也取得了一些有关“北极航道”的技术层面的研究成果。有关航道软科学方面的研究起步则更晚,最早的研究成果出现于2009年,但数量相对较少。综合来看,大量的研究内容涉及到“北极航道”的地缘政治、通航环境、航运价值和国际合作机制等。而有关“北极航道”与贸易增长潜力相关关系的文献资料还是非常少的,这方面研究在国外学术界中鲜有涉及,国内学术界中也只有个别学者进行了此方面的探讨,且都是基于贸易引力模型。

杨晓丹[2]基于传统的贸易引力模型,采用2010年114个国家的横截面数据从货物贸易和服务贸易两个角度定量分析了“北极航道”开通对中国贸易格局的影响,指出“北极航道”开通将使中国2010年的出口贸易总额增长12.67%,同时中国的主要贸易伙伴国的排序将发生改变。贺书锋等[3]将引力模型与随机前沿效率模型相结合,在引力模型原有参数的基础上,增加了贸易互补性指数、共同语言、共同边界等参数,以69个国家1995—2010年的数据作为样本,对“北极航道”的贸易潜力进行了评估。结果表明,中国的出口贸易效率和总贸易效率分别为0.73和0.22,与航运距离显著负相关;“北极航道”开通将使中国的出口潜力和进出口潜力分别提升10.5%和28.1%。孙艺萌[4]基于贺书锋的随机前沿引力模型,剔除了是否有共同边界的参数同时增加了是否为APEC成员等参数,以79个国家2003—2012年的面板数据为样本,量化评估了“北极航道”开通对中国贸易潜力的影响。结果表明,以2012年为基础,“北极航道”开通将使中国的出口潜力和进出口潜力分别提升12.85%和8.48%。

上述学者都是以航运距离作为主要参数来预测“北极航道”开通对中国贸易潜力的影响。本文试图以航行时间替代航运距离,并且考虑了有无海冰因素的影响,对传统的贸易引力模型进行了修正,合理地预测“北极航道”开通对中国及其受影响区域的贸易潜力的影响。

1 基本假设与模型构建

1.1 传统引力模型的引入

传统引力模型最早由Tinbergen和Pöyhönen于20世纪60年代初提出,其核心思想是两个国家之间的贸易流量与它们的经济规模成正比,与它们之间的距离成反比[5-6]。其在经济学中最早的应用形式如下:

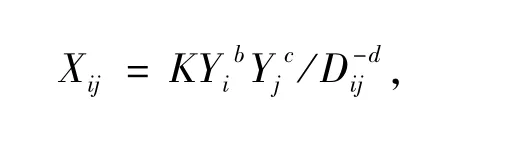
其中,Xij表示i国对j国的出口额,K为常数,Yi和Yj分别表示i国GDP与j国GDP,Dij表示两国之间的距离,一般用两国首都之间的球面距离或者两国港口之间的海运距离来表示。可对该方程两边取自然对数转换为线性形式,即:

lnXij=θ0+θ1ln(YiYj)+θ2ln(Dij)+ε(其中 θ1、θ2为系数,ε为随机干扰项)

此后,学者们对该模型的修正主要通过引入新的解释变量,比如人口、人均GDP等影响贸易额的内生变量和优惠贸易协定、共同语言等虚拟变量。

1.2 基本假设

本文以航行时间替代航运距离对模型进行修正,主要基于以下考虑。

其一,航行时间和航运距离都可以用来表示运输成本。因为海运距离越长,在相同的航速下航行时间也会越长,所需要的燃油费、船员薪资费、操作管理费等就会相应增多,运输成本也会增高。

其二,在通常情况下,船舶经过传统航线一般都存在航期的等待和延误。船舶等待时间延长势必会发生相应的港务费、待泊费等,使得运输成本相应增加。

其三,海冰的存在是影响北极航道运输成本的主要因素[7],其对贸易潜力的影响无法通过距离却可以通过航行时间来体现。因为海冰会使航速降低、航行时间相对延长,进而影响两国之间的贸易交流。

因此,在对传统的贸易引力模型进行修正时,做出进一步假设。

假设1:不考虑巴拿马运河和苏伊士运河两条航线通航能力的差别,将船舶经过这两条航线的在港等待时间统一假定为48 h。

一般情况下,巴拿马运河的通航能力是每天40艘,然而,每天等待通行的船舶有近100艘,如果船舶未提前预定泊位,则需要在港等待3—4天[8];而苏伊士运河目前日均船舶通过量仅有23艘,平均通行时间为20 h,船舶在港等待时间约11 h[9]。因此,在不考虑两条航线通航能力差异的基础上,将船舶经过这两条航线的在港等待时间统一假定为48 h。

假设2:鉴于世界三大类型的海船的航速存在差异,在对其船速进行加权平均的基础上,将经过传统航线的船舶的平均航速假定为16节。

目前,在国际航运业中,主要有三大类型的海船:散货船、油船和集装箱船。据英国劳氏船级社统计,这三大船型在世界船舶总量中的占比高达90%。在三大类型的海船中,每种船型的航速各有差异,其中,散货船和油船的航速较慢,一般为13—17节;集装箱船航速较快,目前最快的可达24.5节。根据航运经济与物流研究所的统计数据,2013年,世界商船队拥有的散货船共计62 207.9万载重吨,油船共计43 511.4万载重吨,集装箱船共计21 566.9万载重吨[10]。由于船舶的航速具有随机性,因此,本文使用随机数生成器对三大类型的海船的航速分别进行10 000次模拟,得出其随机航速分别为15.4节、15.1节和20.5节,在此基础上,根据船型保有量对其进行加权平均,求得经过传统航线的三大类型的海船的平均航速约为16节。

1.3 模型构建

基于上述基本假设,本文对已有的贸易引力模型进行修正,具体如下:

模型1:在考虑船舶等待时间的条件下,将模型设定为:

模型2:不考虑船舶等待时间的条件下,将模型设定为:

在模型1和模型2中:Tijt表示中国对j国第t期的进出口贸易总额;Yit和Yjt分别表示中国第t期的GDP与j国第t期的GDP,反映两国经济规模;H1ijt、H2ijt表示船舶在两国代表性港口之间的航行时间,H1ijt包括等待时间,H2ijt不包括等待时间;TCijt表示贸易互补性指数,可以反映两国经济发展水平的互补和互需程度;FDIit表示中国第t期的外商直接投资总额,FDI可以通过创造新的贸易机会拉动进出口总额的增长;

Nit和Njt分别表示中国第t期的人口数量与j国第t期的人口数量,Gijt表示两国人均GDP取LOG后之差的绝对值,绝对值越小表示两国的经济发展水平越接近,需求偏好越相似,发生产业内贸易的可能性越大;Agreeijt为虚拟变量,表示两国第t期是否有已生效的自由贸易协定,是取1否取0,反映贸易壁垒的大小;WTOijt为虚拟变量,表示两国第t期是否同时为WTO成员国,是取1否取0,衡量入世对双边贸易的重要影响;ε为随机干扰项。

2 模型估计与结果分析

2.1 样本选取与数据说明

本文将利用1995—2013年中国与47个国家/地区的进出口贸易总额作为被解释变量进行回归分析。选取的国家/地区分布在各个大洲,其中亚洲15个、欧洲23个、北美洲3个、南美洲4个、非洲1个、大洋洲1个,2013年这些国家/地区进出口贸易总额都位于世界前50名,更能客观地反映海运距离与贸易流量之间的关系。

在解释变量中,贸易流量(出口额和进口额)的数据来自联合国商品贸易统计数据库;各样本国家或地区的GDP数据、人口数据以及中国的FDI数据来自世界银行数据库;中国(以上海港为代表)与目标国代表性港口之间的海运距离通过Dataloy网站查询所得,其中,由于美国、加拿大和俄罗斯的国土面积较大,且有东西航线之分,所以中国与美国、加拿大和俄罗斯的航行距离分别由上海至洛杉矶、纽约,上海至温哥华、多伦多,上海至海参崴、圣彼得堡的航行距离简单平均得到;航行时间(小时)按以下方法计算所得:H1ijt包括等待时间——中国至各目标国的船舶若不经苏伊士运河或巴拿马运河,其航行时间为传统航线航行距离除以航速16节,若经苏伊士运河或巴拿马运河,其航行时间则需再加上48 h(其中,由于中国至美国、加拿大和俄罗斯的航行距离是东西航线的平均距离,因此船舶的等待时间只需加24 h即可),H2ijt不包括等待时间——无论船舶是否经过苏伊士运河或巴拿马运河,其航行时间都等于传统航线航行距离除以航速16节;贸易互补性指数数据(四位HS编码)来源于WITS网站;自由贸易协定(Agree)相关信息来源于联合国世界区域贸易协定的统计;WTO相关信息来自世界贸易组织网站的成员统计。

2.2 面板数据的检验

在计量经济学中,为了避免“伪回归”的出现,确保估计结果的有效性,通常要对时间序列数据和面板数据进行平稳性分析,即通过单位根检验和协整检验来检验数据过程是否平稳,是否存在稳定的协整关系。

2.2.1 单位根检验

单位根检验的方法分为两大类,分别是针对同质面板假设的LLC、Breintung方法和针对异质面板假设的IPS、ADF-Fisher和PP-Fisher方法。为使检验结果具备较强的稳健性和说服力,本文同时采用LLC检验和Fisher-ADF检验,如果在两种检验中均拒绝存在单位根的原假设,我们就说此序列是平稳的,反之则不平稳。检验结果如表1所示。

表1 面板数据单位根检验结果Table 1.Unit root test results for panel data

由表1结果可知,所有变量均不能在10%的显著性水平下拒绝存在单位根的原假设;但是各变量经过一阶差分后,平稳性显著增强,均能在1%的显著性水平下拒绝原假设,因此所有变量都是一阶单整的非平稳序列。

2.2.2 协整检验

由单位根检验结果得出模型各变量同阶单整的结论,满足面板协整检验的要求。所谓协整,是指多个非平稳经济变量的某种线性组合是平稳的,反映了变量之间一种长期稳定的均衡关系。本文采用基于残差的 Kao检验对变量 lnTijt、ln(Yit*Yjt)、lnTCijt、lnFDIijt与lnGijt之间的协整性进行检验,两模型所得到的统计值ADF均为-13.735 3,在1%的置信度水平上显著,可以拒绝无协整的原假设,说明模型中以上变量之间存在长期稳定的均衡关系。

2.3 模型回归与结果分析

2.3.1 模型回归

经过上述单位根检验和协整检验,就可以对模型进行回归。为了消除特定个体残差在时间上存在的序列相关性和异方差,本文采用时期似不相关的截面加权广义最小二乘法(即EGLS加权项设为“Period SUR”)进行回归,估计结果如下。

其中,R2=0.747 8AD(R2)=0.745 8F=374.849 0D.W.=1.993 3

从模型1和模型2的回归结果可知:调整后的R2分别为0.718 3和0.745 8,说明回归方程的拟合优度较好;F值分别为325.990 7和374.849 0,远远大于F统计量的临界值F(k,n-k-1)=F(7,39)=1.87,可知回归方程拒绝零假设,表明各自变量联合对因变量有显著的线性影响;D.W.值分别为2.009 6和1.993 3,非常接近2,说明模型中不存在序列相关性;各变量系数都通过了5%置信度水平上的显著性检验,且输出结果与经济学意义相吻合。

结合图1、图2可以看出,两模型的拟合优度很好,残差序列十分平稳,lnTijt的实际值与预测值非常接近,可以用来预测中国的对外贸易流量。

图1 模型1的实际值、预测值及残差走势Fig.1.Residual,actual and fitted in model one

图2 模型2的实际值、预测值及残差走势Fig.2.Residual,actual and fitted inmodel two

2.3.2 结果分析

模型1和模型2的回归结果表明,中国与目标国之间GDP的乘积、中国的外商直接投资总额以及两国的贸易互补性指数、两国之间是否签订自由贸易协定、两国是否同时为WTO成员这几个变量与进出口总额之间呈正相关关系,航行时间和经济发展水平的差异这两个变量与进出口总额之间呈负相关关系,该结果与预期结果一致。其中,GDP的弹性较大,在航行时间等其他变量保持不变的情况下,中国与目标国之间GDP的乘数效应每增加1%,中国对该国的进出口总额分别会增加0.875 2%和0.884 1%,表明两国的经济发展水平越高、两国之间的贸易规模就会越大;FDI的弹性分别为1.018 7和1.002 8,甚至高于GDP对贸易额的影响,因为中国FDI企业较强的进口意向和极强的外向拓展能力带动了中国进出口贸易的高速增长,这也支持了日本经济学家小岛清于1987年提出的国际直接投资创造新的国际贸易机会的观点;贸易互补性指数(TC)的系数显示较强的显著性,与其他实证结果一致,表明两国之间经济发展的互补互需程度越高、两国之间的贸易交流越多;自由贸易协定(Agree)和世贸组织成员(WTO)变量也都有显著的正弹性;经济发展水平的差异的弹性分别为-0.035 8和-0.039 3,虽然其对贸易额的影响不是太大,但是通过了显著性检验,说明两个国家经济发展水平差异越小,两国之间发生产业内贸易的可能性越大,这就是所谓的“林德效应”。

在模型1和模型2中,航行时间的回归系数分别为-0.659 0和-0.807 1,该结果表明:在两国经济发展水平、贸易互补性程度等其他变量保持不变的情况下,若考虑船舶等待时间,中国到目标国代表性港口之间的航行时间每减少1%,中国对该国的进出口额就会增加0.659 0%;若不考虑船舶等待时间,中国到目标国代表性港口之间的航行时间每减少1%,中国对该国的进出口额就会增加0.807 1%。考虑到传统航线存在船舶等待这个客观事实,本文将采用模型1的回归结果来预测“北极航道”开通对贸易潜力的影响。因为采用模型2的回归结果将会忽略船舶在港等待期间发生的成本和费用,进而会高估“北极航道”开通对贸易潜力的提升作用,而模型1则可以更客观地反映实际发生的运输成本和贸易额之间的关系,也有利于客观地评价“北极航道”开通的潜在贸易价值,因此下文将以模型1的结果为依据进行贸易潜力的评估。

3 “北极航道”的潜在贸易价值评估

“北极航道”开通将大大缩短中国至欧洲和北美的航行距离,这不仅使其运输成本和贸易成本降低,而且还会对中欧、中美之间的贸易潜力产生较大影响。然而,与传统航线相比,“北极航道”又具有其特殊性,即海冰的存在会降低船舶航行的经济效益,进而影响贸易成本。目前,“北极航道”尚未全面开通,其通航期仅为3—5个月,即使是通航条件非常优越的8—10月份,北极“东北航道”和“西北航道”的部分海域仍会有不少浮冰存在。

“北极航道”未来真正适于商业通航的时间主要取决于北冰洋出现第一个夏季无冰年的时间。而专家预测北冰洋出现第一个夏季无冰年的时间不断提前,最新预测结果表明,北极首个夏季无冰年可能在2020年前出现。这充分证明,未来“北极航道”实现夏季全面通航是极有可能的。因此,根据“北极航道”当前的通航形势和未来的通航前景,本文将考虑存在海冰因素影响和不存在海冰因素影响两种情况,对其给中国及受影响区域带来的贸易增长潜力进行评估。

3.1 存在海冰情况下“北极航道”的潜在贸易价值评估

3.1.1 存在海冰时“北极航道”船舶航速的确定

根据船舶主机燃料消耗率的计算公式:F=FP·m·V3(F指船舶的主机燃料消耗率;FP指船舶主机的单位功率燃料消耗率;V指航速;m是大于零的比例系数),船舶主机的燃油消耗率与航速的三次方成正比[11],当航速降低的时候,燃料消耗率也会降低。

在存在海冰的情况下,船舶在“北极航道”航行时航速会降低,从而导致船舶主机的燃油消耗率降低。但是,在“北极航道”航行的船舶一般都需要有破冰能力,对船舶主机的单位功率要求会提高;而船舶主机的单位功率提高,又会使船舶主机的燃油消耗率增加。因此,存在海冰的情况下,船舶的航速对船舶主机的燃油消耗率的影响实际上是不确定的。鉴于此,在存在海冰因素时,本文不考虑航速与燃油消耗率的关系,只考虑航行时间对运输成本的影响。这样,船舶在“北极航道”航行时,其航行时间就成为影响运输成本的主要因素。而航行时间又主要受船舶航速的影响,因此,在考虑海冰影响的情况下,评估“北极航道”的潜在贸易价值,必须确定船舶受海冰影响时的航速,此航速与冰值之间存在着较大的关系。

根据北极冰情运输系统(AIRSS),北极海冰依据其发展阶段和密度可以分为新冰、灰冰、灰白冰等九种不同类型,不同类型的海冰对应着不同的密集度和倍数值。而冰值(IN)的计算公式为:IN=(CaIMa)+(CbIMb)+…+(CnIMn)[12],其中Ca为a种类型冰的密集度,取值为0—10,值越大表示海冰的密集度越小;IMa为a种类型冰的倍数值,取值为-4至2,值越大表示海冰的厚度越小。当MAX(Cn)=10,MAX(IMn)=2时,IN的最大值为20,航行条件达到最优。McCallum[13]通过分析冰值和冰区船舶之间的关系,给出了在不同的海冰状况下冰级船舶的安全航速,当冰值达到最大时,船舶的安全航速应保持在7—16.5节,如图3所示。

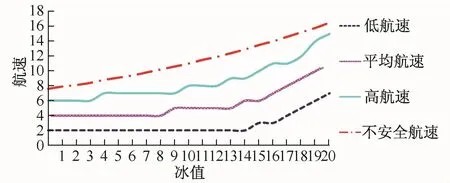
图3 船舶在海冰环境中的航速.数据取自文献[13]Fig.3.The speed of ships in ice environment.Data from[13]

中国“永盛轮”在“北极航道”的首次商业航行实践很好地验证了上述理论研究结果。2013年,中国“永盛轮”从太仓港出发,经“北极航道”东北航道,到达荷兰鹿特丹,总航程793 1海里,航行时间为27天,平均航速约12.24节;而永盛轮是一艘多用途船舶,其总载重量为1.9万吨,设计航速为14节。考虑到未来北极气候的变化以及造船技术和航海技术的提高,结合中国永盛轮的商业航行实践和McCallum的理论研究结果,为了能够科学地评估存在海冰情况下中国及其受影响区域的贸易增长潜力,本文将船舶在“北极航道”的平均航速合理地假定为13节。

3.1.2 存在海冰情况下中国的贸易增长潜力评估

在上述假定的基础上,存在海冰的情况下,船舶在传统航线的航速为16节,在“北极航道”的航速为13节,而从中国上海港出发经传统航线和“北极航道”到欧美各目标国的代表性港口之间的航行距离可以通过Dataloy网站(http://www.dataloy.com)查询。由于上海港位居中国18 000 km大陆海岸线的中部,地处长江东西黄金水道与海上南北运输通道的交汇处,是中国参与国际经济大循环的最重要的口岸,而且上海港已连续多年成为世界货物和集装箱吞吐量第一大港。因此,本文在上述已修正的引力模型的基础上,以上海港为代表,以上海港经“北极航道”到各目标国的航行时间作为主要参数来对中国的贸易增长潜力进行评估。

经计算发现,船舶经“北极航道”比经传统航线可以较大幅度地缩短航行时间。根据模型1的回归结果表明:在两国经济规模等其他条件保持不变的情况下,中国到目标国之间的航行时间每减少1%,中国对该国的进出口总额就会增加0.659 0%。因此,在样本国家中,中国与北极航线上的各目标国之间的贸易增长潜力如表2所示。

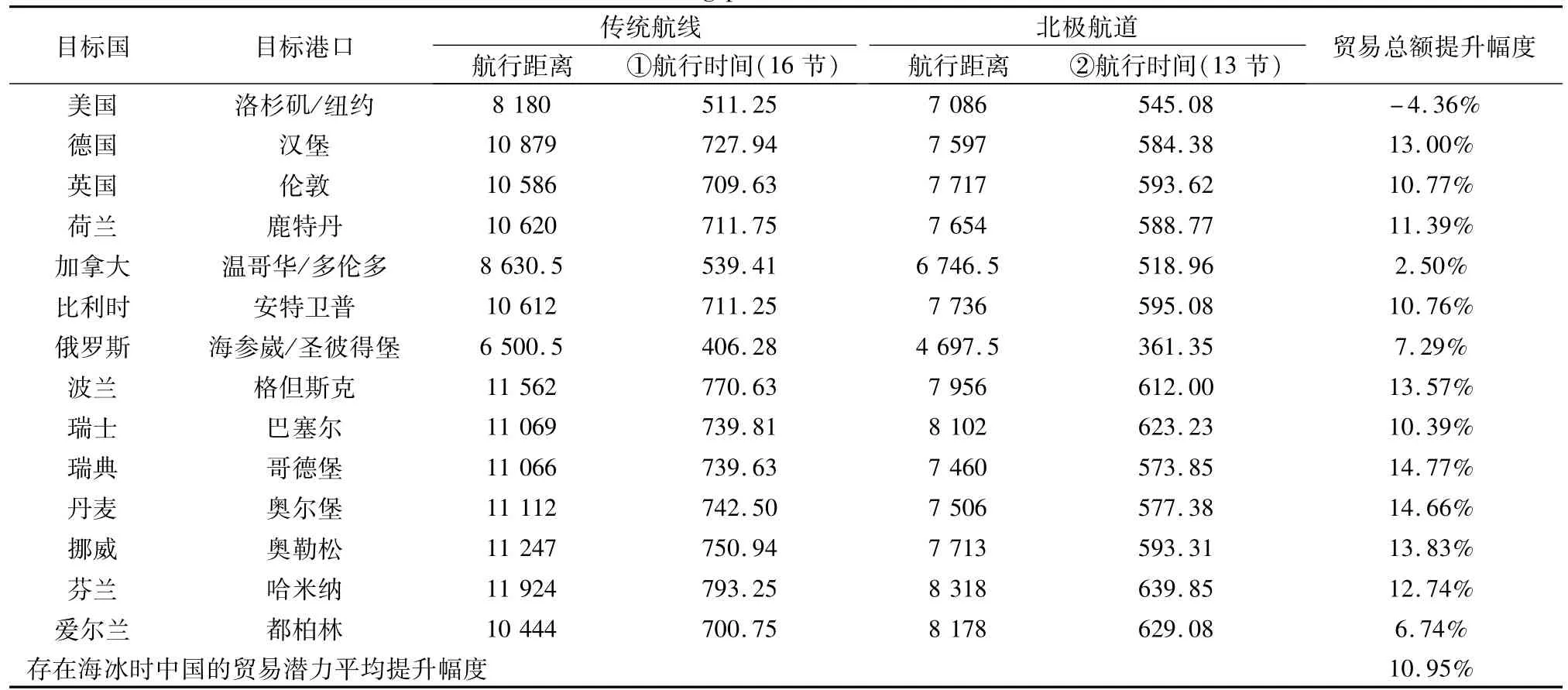
表2 存在海冰情况下中国的贸易增长潜力Table 2.Trade enhancing potential for China with sea ice factor

由上表可知,在存在海冰情况下,中国与主要目标国的进出口潜力最高可提升14.66%(目标国为瑞典,目标港口为哥德堡),平均可提升10.95%,因此,“北极航道”的开通大大地提升了中国的贸易增长潜力。其中,存在海冰时中国与北极“西北航道”上的美国、加拿大之间的贸易额增长效应分别为-4.36%、2.50%,相对于“东北航道”上的各目标国来说,其增长幅度十分有限,主要因为中美、中加之间的海运距离是以北美洲东、西航线的平均距离来计算的,降低了“北极航道”的影响。

3.1.3 存在海冰情况下中国受“北极航道”影响区域的贸易增长潜力评估

“北极航道”开通不仅使中国整个国家的贸易潜力大幅增长,而且也会给中国沿海地区,尤其是北部沿海地区等受影响区域带来新的贸易增长空间和经济发展机会[14]。本文将“受影响区域”划分为三大地区,即北部沿海地区(辽宁、河北、天津、山东)、东部沿海地区(江苏、上海、浙江)和南部沿海地区(福建、广东、海南、广西),并分别对比分析这三大地区的贸易增长潜力。

在计算受影响区域的一些代表性港口(大连、秦皇岛、新港、青岛、连云港、上海、宁波、厦门、广州、海口、防城港)经“北极航道”到各目标国港口的航行时间的基础上,结合模型1的回归结果,得出了以这些港口为代表的各省(市)的对外贸易潜力,并通过对区域内的各省(市)的贸易潜力进行简单平均,求出三大沿海地区的贸易潜力的平均提升效应,如表3所示。

表3 存在海冰情况下受影响区域与各目标国之间的贸易增长潜力(%)Table 3.Trade enhancing potential for China′s coastal areas with sea ice factor(%)

由表3可知,在存在海冰的情况下,中国北部沿海地区和东部沿海地区受“北极航道”的影响比较显著,与各目标国之间的贸易潜力平均提升幅度分别为12.02%和11.22%,且其区域内的各省(市)的贸易增长潜力也都在10.51%—12.41%之间,相差不大;而南部沿海地区受“北极航道”的影响相对较弱,与各目标国之间的贸易潜力平均提升幅度仅为3.37%,且其区域内的福建、广东、海南和广西的贸易增长潜力分别为6.15%、3.87%、1.78%和1.69%,差异比较明显。这充分说明,在存在海冰的情况下,相对于中国南部沿海地区而言,北部沿海地区和东部沿海地区利用“北极航道”的优势更加明显。

3.2 不存在海冰情况下“北极航道”的潜在贸易价值评估

3.2.1 不存在海冰情况下中国的贸易增长潜力评估

随着全球气候变暖,北极海冰的覆盖范围会越来越小。一旦海冰消融,“北极航道”的通航优势则会更加凸显,给中国及其受影响区域的贸易潜力也会带来更大幅度的提升。

不存在海冰的情况下,船舶在“北极航道”的航速应与传统航线相同,都为16节,中国与各目标国的贸易增长潜力如表4所示。

表4 不存在海冰情况下中国的贸易增长潜力Table 4.Trade enhancing potential for China without sea ice factor

对照表4和表2,船舶经“北极航道”的航行时间进一步减少,中国与各目标国之间的贸易增长潜力也进一步上升。其中,中国与瑞典之间的贸易增长潜力达到24.36%,而存在海冰的情况下仅为14.66%;中国与美国之间的贸易增长潜力由-4.36%变为8.81%,说明存在海冰的情况下“西北航道”对于中美之间的贸易影响不大,而不存在海冰的情况下可以从中节约更多的运输成本,因而“西北航道”此时对于中美贸易的影响较大。总之,与当前的航运形势相比,未来不存在海冰的情况下,中国的贸易增长潜力会得到进一步提升。

3.2.2 不存在海冰情况下中国受“北极航道”影响区域的贸易增长潜力评估

根据上文的研究结果,存在海冰影响时,中国北部沿海地区、东部沿海地区和南部沿海地区的贸易增长潜力分别为12.02%、11.22%和3.37%。依据同样的计算方法,可求得不存在海冰的情况下中国受影响区域的贸易增长潜力,如表5所示。

表5 不存在海冰情况下受影响区域与各目标国之间的贸易增长潜力(%)Table 5.Trade enhancing potential for China’s coastal areas without sea ice factor(%)

由表5可知,不存在海冰影响时,北部沿海地区和东部沿海地区的贸易增长潜力分别为21.21%和20.57%,与存在海冰的情况相比,分别进一步提升了9.19%和9.35%;而南部沿海地区的贸易增长潜力为13.83%,与存在海冰的情况相比,进一步提升了10.46%。这充分说明,海冰因素会对中国受影响区域的贸易增长潜力产生较大影响,未来“北极航道”实现全面通航时,中国沿海地区的贸易额提升效应会进一步增加,增加一倍甚至还多。

总之,无论是否存在海冰的影响,以上的研究结果都证明,中国北部沿海地区和东部沿海地区的贸易增长潜力都高于南部沿海地区,将从“北极航道”的开通中获得更大的地缘优势。图4显示了存在海冰情况下和不存在海冰情况下中国受影响区域的贸易增长潜力的对比。

图4 中国受影响区域的贸易潜力的平均提升效应Fig.4.Average promotion effect of trade volume for China′s affected areas

4 结论

北极航道的开通不仅可以大大降低中国海外贸易的运输成本,而且还将影响中国区域经济发展格局,给中国东部沿海特别是北部沿海地区带来新的经济发展和增长机会。

中国与欧洲、北美的贸易量非常大,年贸易额分别位居世界第一和第二,这些贸易量主要通过海洋运输来完成。开辟北极新航线可以大幅度节省海运里程,降低海运成本,从而进一步促进中国与欧洲和北美的贸易。在存在海冰的情况下,中国与欧美各目标国的贸易潜力平均可提升10.95%;一旦海冰消融、“北极航道”实现全面通航,中国与欧美各目标国的贸易潜力则会进一步提升到20.37%。同时,根据中国的区域经济布局,东部沿海地区由于拥有能够直接连接到世界各大经济区域的海洋通道,具有独特的地缘经济优势,“北极航道”的开通将进一步加强这一优势,为东部沿海带来新的经济增长和发展机会。尤其是中国北部沿海地区离北极地区相对较近,“北极航道”的开通将使北部沿海地区的优势得以显现,从中获得更大的发展机遇。

1 巴伦支海观察员网站http://barentsobserver.com/en/sections/arctic.

2 杨晓丹.北冰洋新航道开通对我国贸易格局的影响——基于引力模型及厂商异质理论的分析.上海:华东师范大学,2012.

3 贺书锋,平瑛,张伟华.北极航道对中国贸易潜力的影响——基于随机前沿引力模型的实证研究.国际贸易问题,2013,(8):3—12.

4 孙艺萌.北极航线对我国对外贸易潜力的影响研究.辽宁:大连海事大学,2014.

5 Tinbergen J.Shaping the world economy:suggestions for an international economic policy.New York:The Twentieth Century Fund,1962.

6 Pöyhönen P.A tentativemodel for the volume of trade between countries.Weltwirtschaftliches Archiv,1963,90(1):93—99.

7 张爱锋,宋艳平.基于海冰影响的北极航线经济性研究.大连海事大学学报,2014,(5):43—46.

8 李震.巴拿马运河扩建对航运市场的影响.辽宁:大连海事大学,2010.

9 http://www.chinadaily.com.cn/micro-reading/dzh/2014-08-07/content-12152429.html.

10 李源,秦琦,祁斌,等.2013年世界船舶市场评述与未来展望.船舶,2014,(1):1—12.

11 Cullinane K,Khanna M.Economies of scale in large containerships:Optimal size and geographical implications.Journal of Transport Geography,2000,8(3):181—195.

12 Arctic Ice Regime Shipping System(AIRSS)Standards-TP12259.Transport Canada,2012.http://www.tc.gc.ca/eng/marinesafety/tp-tp12259-arctic-ice-regime-2871.htm#n5.

13 ENFOTEC Technical Services Inc,Geolnfo Solutions Ltd,John McCallum.Safe speed in ice:an analysisof transit speed and ice decision numerals.Ship Safety Northern(AMNS)(Transport Canada Ottawa),1996.

14 张侠,屠景芳,郭培清,等.北极航线的海运经济潜力评估及其对我国经济发展的战略意义.中国软科学,2009,S2:86—93.