利用GPS技术遥感北极黄河站可降水量的研究

张胜凯 赵云，2 鄂栋臣 宁新国 徐优伟 雷锦韬

(1武汉大学，中国南极测绘研究中心，湖北武汉430079;2济南市勘察测绘研究院，山东济南250013)

0 引言

GPS气象学(GPSMeteorology)是近十几年来蓬勃发展起来的一门新兴边缘学科。1987年，美国Askne等［1］在该领域做了理论奠基工作，提出了GPS遥测大气的设想，导出了大气湿延迟与可降水量的关系。1992年，Bevis等［2］进行了大量研究，提出了地基GPS遥感大气可降水量的原理和方法。从20世纪90年代起，许多国家先后进行了一系列地基GPS遥感大气的实验和研究，如美国著名的GPS/STORM实验［3］，德国、日本和荷兰成功组织了数次较大规模的实验观测，取得了一系列研究成果，并被用于气象服务中［4］。中国早在90年代初，根据GPS/MET原理与方法，利用地基GPS手段反演大气参数，如上海地区GPS/STORM实验、华南地区GPS降雨观测实验、北京地区GPS/VAPOR观测实验等［5-7］。目前GPS遥感大气可降水量的技术在全球范围内得到了广泛应用，其公认的精度为1-2 mm［8］。

北极是地球三极之一，是地球上的气候敏感地区，大部分地区终年为冰雪所覆盖，对全球气候变化有着一种指示和调控作用，也是多个国家科学计划研究全球气候变化的关键地区［9-11］。北极黄河站位于78°55'N、11°56'E，坐落于挪威斯匹次卑尔根群岛的新奥尔松，没有明显的春季和秋季，属于典型的苔原气候和海洋性气候，较多雾。由于受到流经群岛的北大西洋暖流影响，该地区的气温较北极其他地区要高，年平均气温为-4℃［12］。由于其地处北半球高纬度地区，是全球气候变化研究板块中不可缺少的一环，北极地区的变化，将影响着全球环境和气候［13］，所以利用GPS技术遥感北极黄河站可降水量对全球气候变化研究具有重要意义。

1 利用GPS数据反演黄河站的大气可降水量

为反演大气可降水量，我们需要知道高精度的天顶湿延迟ZWD(Zenith Wet Delay)、对流层天顶湿延迟可由天顶总延迟ZTD(Zenith Total Delay)和天顶干延迟ZHD(Zenith Hydrostatic Delay)之差来间接计算，即:

得到ZWD后再经过相应的转换公式即可解算出可降水量 PWV，计算公式为［14］:

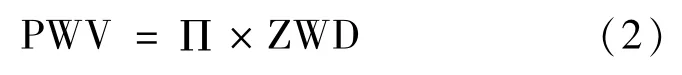
式中无量纲转换因子∏近似值为0.15，其实际计算公式为［15］:

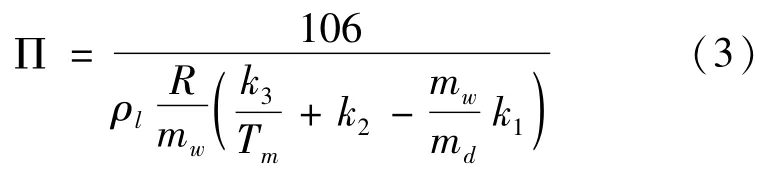
其中，ρl为液态水的密度，k1、k2、k3分别为常数，md、mw分别为干大气和水汽的摩尔质量，R为普适气体常数，Tm为大气加权平均温度，值随季节和地区(或气候区)而变，统计显示其值与地面气温呈现高度的线性相关，两者的回归关系式为:

此式也被称为Bevis经验公式，是根据美国27°N-65°N地区两年8 718次探空资料统计而得到，一般取 a=70.2，b=0.72［16］。

2 GPS反演大气可降水量精度分析

由式(1)可知，天顶湿延迟的计算精度取决于大气总延迟ZTD、大气干延迟ZHD的精度，其误差关系式为:

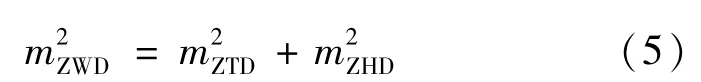
由式(2)可知，可降水量的精度取决于湿延迟转换因子∏和天顶湿延迟ZWD的精度，而在式(3)中，令，对其进行微分并简化后得:

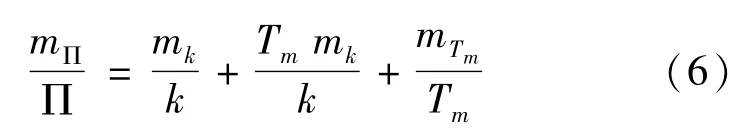
通过计算可知，上式中右边第三项远大于第一项和第二项［17］，因此式(7)可以简化为:

这表明大气加权平均温度的Tm的相对误差和转换因子∏的相对误差是基本相同的，只要能正确求出Tm值就能确保转换因子的精度。

因此，为评定可降水量的计算精度，需首先确保天顶总延迟ZTD、天顶干延迟ZHD以及大气加权平均温度Tm的精度，下面对此三项分别进行分析。

2.1 ZTD的估计及精度评定

在地基GPS遥感水汽过程中首先利用地基GPS观测数据计算高精度的对流层天顶总延迟ZTD，因为高精度的ZTD是后续计算PWV的基础。为了检验ZTD估计结果的精度和可靠性，本文利用GAMIT软件［18］平台估算ZTD，并把解算结果与IGS分析中心的结果进行了对比。本文后续所有采用GAMIT解算的参数设置如表1所示。

表1 GAM IT解算ZTD参数设置Table 1.Parameters of calculating ZTD by using GAMIT

本算例采用了黄河站及其周边9个IGS站(NYAL、RESO、THU3、SCOR、HOFN、MORP、TRO1、NRIL、TIXI)连续 10 d(年积日 2010.002-2010.011)的GPS观测数据进行联网解算。为了检核算例TEST的外符合精度，将IGS分析中心JPL的ZTD结果作为真值参考值，以距离黄河站1.7 km处的IGS站NYAL站为分析对象，图1为本文TEST算例与IGS分析中心JPL计算ZTD的结果对比图。

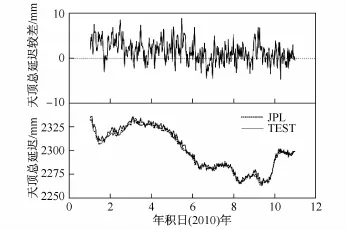
图1 NYAL站TEST与IGS分析中心JPL计算ZTD的比较Fig.1.Comparison of ZTD calculated by TEST and IGSanalysis center JPL in NYAL Station

经统计分析可得TEST算例与IGS分析中心JPL估算ZTD结果的误差如表2所示。

表2 ZTD误差统计结果Table 2.Error statistical results of ZTD

从结果上看，两者计算的ZTD具有相同的趋势，且精度优于3 mm，这就使得计算PWV的精度可以优于1 mm。因此可以认为本文采用GAMIT解算的ZTD是可靠的，可以用作后续的实验研究和数据分析。

2.2 ZHD的估计及精度评定

在GPS反演大气可降水的过程中，一般采用的是“普适性”模型，如Saastamoinen模型、Hopfield模型和Black模型。在这些模型中，干延迟的改正公式都是在理想化的大气条件下推导出来的，如假设气温以常数随高度递减，水汽压随高度减小服从指数定律等。“普适性”模型计算出的ZHD值精度如何，特别是在高纬度地区能否适用，这是我们需要验证的问题。

大气干延迟的实际计算公式可表示为:

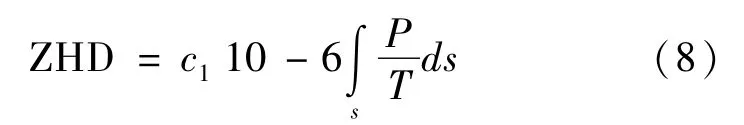
式中c1为常数，P为压强(hPa)，T为温度(K)，ds为积分路径(m)，有了实测探空资料后，就可以利用式(8)进行干延迟计算了。

本文选取了NYA气象站2010年的探空数据，数据包括2010年每天1-2次各等压层的气象资料。大气干延迟主要是由对流层引起的，但是对流层以上的平流层大气对干延迟订正也有15%左右的贡献［19］。在计算实际干延迟时，一般需要从地面计算到100 km高度处，但是探空气球只能到达30 km左右的高空，因此需要根据标准大气进行实测探空资料的续补［20］。

Saastamoinen模型计算干延迟的表达式为［21］:

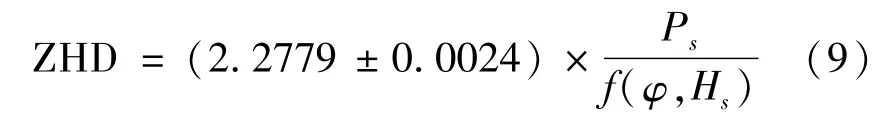
式中f(φ，Hs)=1-0.00266cos(2φ)-0.00028Hs，其中φ为地理纬度，Hs为测站海拔高度(m)，Ps为地面气压(hPa)。

我们选取了黄河站区的雨季即7-9月，分别用续补后的探空数据和Saastamoinen干延迟模型计算了ZHD，绘成图2。

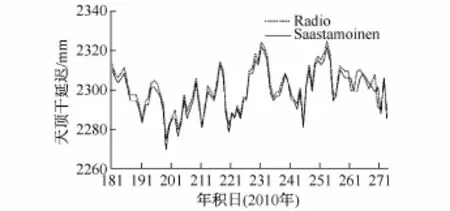
图2 2010年7-9月Saastamoinen干延迟模型与探空数据计算ZHD的比较Fig.2.Comparison of ZHD calculated by Saastamoinen Model and Radiosonde data between July and September in 2010

从图上可以看出，曲线具有相同的走势，且纵坐标差异较小，说明两者计算的结果符合得很好。继而我们计算得到了两者2010年全年的结果，将续补后探空数据计算的ZHD作为真值，计算两者的误差如表3所示。

表3 ZHD误差统计结果Table 3.Error statistical results of ZTD

从统计结果可知，Saastamoinen干延迟模型计算ZHD在黄河站区具有较高的精度，其标准差优于3 mm，使PWV计算的精度可优于1 mm，以满足高精度地基GPS反演大气可降水的要求。

2.3 加权平均温度Tm的局地订正模型

地基GPS反演PWV时普遍采用Bevis经验改正公式来计算Tm，但Bevis公式也是在特定空间范围内建立起来的，黄河站地处高纬度地区，显然不在Bevis公式的适用范围。因此，为了提高GPS反演PWV的精度，有必要对Tm进行局部订正。

目前公认的最精确的计算对流层加权平均温度的方法是探空资料数值积分法［21］，其计算公式为:

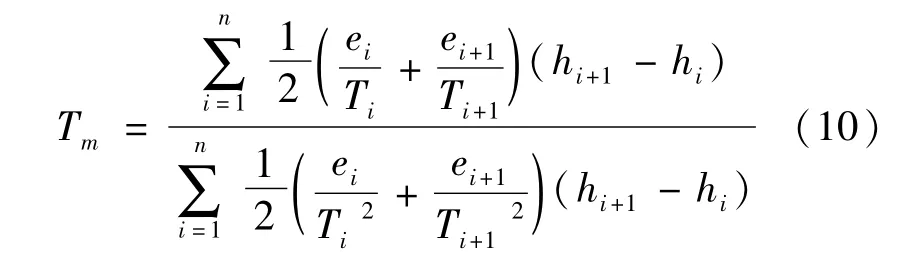
式中，hi+1、hi、ei、ei+1、Ti、Ti+1分别是上下观测层的高度值、水汽压和温度。

本文根据黄河站附近的NYA自动气象站2008-2010年每日1-2次的气象探空观测资料，采用如式(10)所示的数值积分方法计算出这三年的加权平均温度，通过比较分析发现，加权平均温度Tm与地面气温之间Ts存在很好的相关性，两者随时间的演变关系如图3所示:

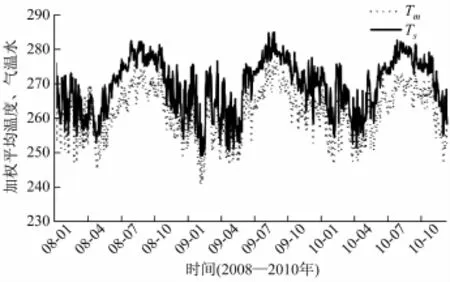
图3 NYA气象站加权平均温度Tm与地面气温Ts随时间的演变关系Fig.3.The time evolution ofweighted mean temperature Tm and surface air temperature Ts in NYA weather station

由图4可知，加权平均温度普遍低于地面气温，但两者的高低值对应很好，且两者的升降趋势及幅度基本一致，呈现明显的正相关;而李建国等［22-23］的研究表明，加权平均温度和地面温度之间存在较好的线性关系。Tm和Ts的线性方程系数，可以用一元线性回归方法求得，

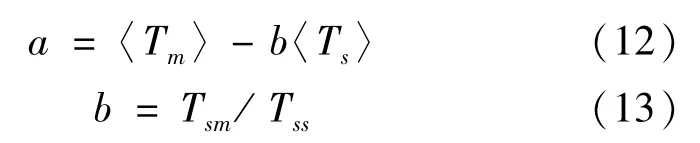
从而得到加权平均温度与地面气温的直线方程，如图4所示。

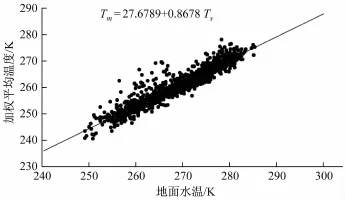
图4 NYA气象站加权平均温度Tm与地面气温Ts的线性关系Fig.4.Linear relationship ofweighted mean temperature Tm and surface temperature Ts in NYA weather station

高精度的GPS可降水反演中，为保证湿延迟量转换为可降水量的精度优于1 mm，对流层加权平均温度的精度要优于3.4 K。而以气象探空计算的Tm为真值，将其与Bevis公式算出的Tm值相减可得出Bevis公式计算加权平均温度的误差。计算得知Bevis公式计算的Tm在黄河站区的标准差为3.853 K，无法满足高精度GPS反演的要求。

而将加权平均温度进行局地改正之后，也以探空计算的Tm为真值，计算得到局地改正模型与Bevis公式的精度对比如下表所示:

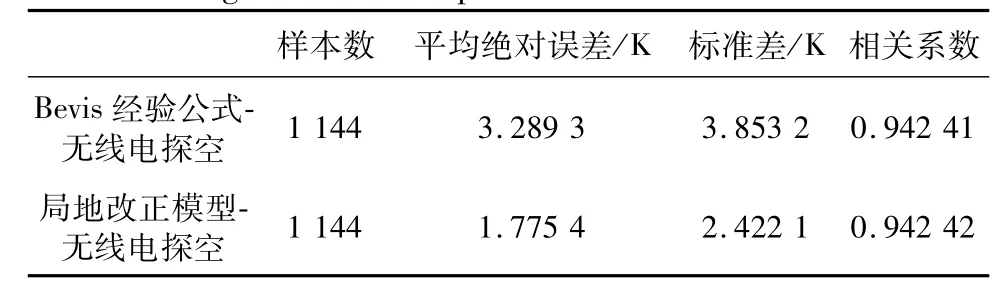
表4 Bevis经验公式、局地改正模型和探空法计算加权平均温度的对比分析Table 4.Comparative analysis of Bevis empirical formula、local correctionmodel and Radiosondemethod in calculating weighted mean temperature

统计结果表明，局地改正模型比Bevis经验公式更加接近探空计算值，且局地改正模型的标准差小于3.4 K，可以满足高精度GPS反演可降水的要求。

3 基线解算和水汽含量对比

3.1 GPS基线解算

本文采用了黄河站GPS常年跟踪站2010年所测得的GPS数据与周边的9个IGS站进行联测解算，使用的软件为麻省理工学院研制的GAMIT/GLOBK，黄河站及9个IGS跟踪站的位置如图5所示(其中CNYR代表黄河站，NYAL由于距离黄河站太近在图上显示为重合在一起)。

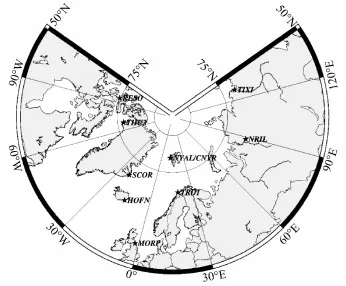
图5 黄河站及周边9个IGS站的位置分布图Fig.5.Position distribution of Yellow River Station and 9 IGS Stations near it

为了验证GPS基线解算的精度，本文计算了基线的重复性和相对重复性，其长基线的相对精度能达到10-9量级，短基线的精度能优于1 mm。继而以基线重复性为观测值，用线性拟合求出重复性的固定误差和比例误差，计算结果如表5所示:

表5 2010年基线重复性统计结果Table 5.Statistical results of baseline repeatability in 2010

由统计结果可知，基线重复性均达到了10-9量级，满足高精度GPS数据处理的要求。

3.2 水汽含量对比

为了验证黄河站可降水量解算结果的可靠性，本文计算了离黄河站1 700 m的IGS站NYAL的可降水量，同时也采集了离黄河站414 m处的NYA气象站的数据，计算得到了无线电探空的可降水值。

若将无线电探空计算的可降水值视为真值，则本文实验中GPS反演的可降水量精度能够优于2个mm。本文首先计算了2010年7-9月黄河站、NYAL和NYA气象站的可降水值，如图6所示(粗实线为NYAL站可降水量)。

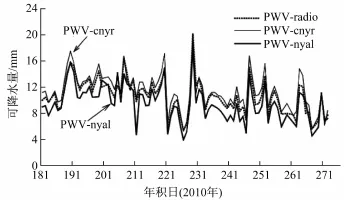
图6 2010年7-9月CNYR、NYA气象站和NYAL可降水量的比较Fig.6.Comparison of PWV in CNYR、NYAWeather Station and NYAL between July and September in 2010

从整体趋势上看，三者的走势保持一致，但黄河站计算的可降水量总体上大于探空计算值，而NYAL站计算的可降水量则小于探空计算值。

将无线电探空计算的可降水值视为真值，则黄河站和NYAL与探空的误差统计结果如下表所示:

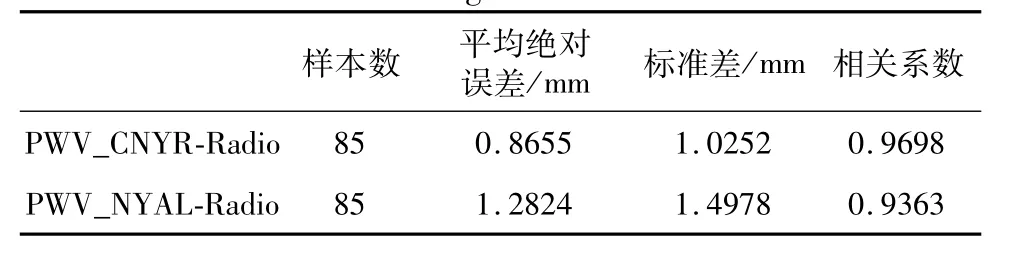
表6 CNYR、NYAL和探空计算PWV值的对比分析Table 6.Comparative analysis of CNYR、NYAL and Radiosonde method in calculating PWV

从统计结果可知，CNYR与NYAL计算PWV值均达到了较高的精度，其标准差优于2个mm，但从数值上看，CNYR计算可降水的精度要略高于NYAL。

同时，为了验证大气加权平均温度局地改正模型的可用性，我们以CNYR为研究对象，用大气加权平均温度局地改正模型替换Bevis模型，计算了2010年全年CNYR(Bevis模型)、CNYR(局地模型)和无线电探空的可降水值，如图7所示(粗实线代表局地模型，Bevis模型和局地模型计算的值比较接近，在图上显示为重合在一起)。

从曲线的整体特征看，北极黄河站区的GPS/PWV值季节变化明显，夏季最大且峰值最高，春、秋季次之，冬季最小。从曲线的走势看，全年PWV值出现多次峰值，整条曲线平滑度低，预示着黄河站区全年下雨次数较多;但由于PWV数值不大，表明雨量较小。

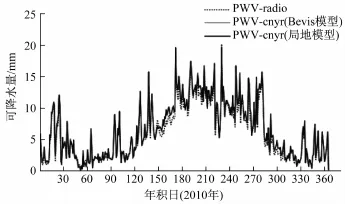
图7 2010年CNYR(Bevis模型)、CNYR(局地模型)和探空计算可降水量的比较Fig.7.Comparison of calculating PWV in CNYR(Bevis Model)、CNYR(local model)and Radiosonde method in 2010

进而我们计算了 CNYR(Bevis模型)、CNYR(局地模型)的可降水量与探空值的误差，统计结果如表7所示。

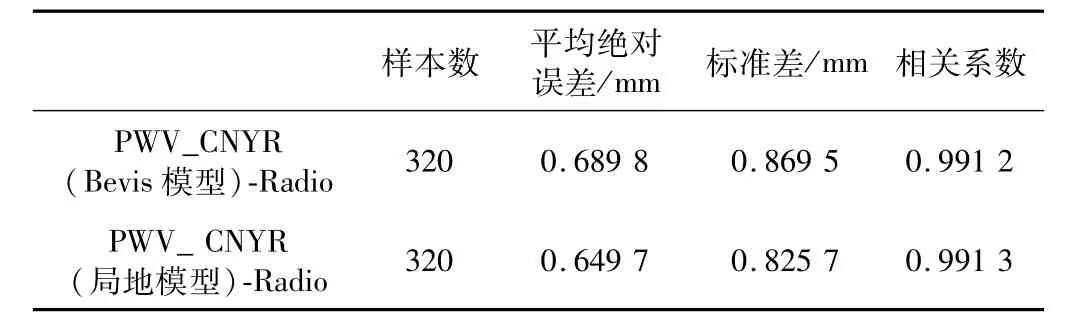
表7 2010年CNYR(Bevis模型)、CNYR(局地模型)和探空计算PWV值的误差统计结果Table 7.Error statistical results of CNYR(Bevis Model)、CNYR(Local Model)and Radiosonde method in calculating PWV

由统计结果可知，加权平均温度局地改正模型比Bevis模型具有更好的精度，证明了其在北极黄河站区的可用性。

4 结论与展望

本文主要采用地基GPS的方法对黄河站可降水量进行了研究，主要工作分为以下几个方面:

(1)将干延迟模型计算的天顶干延迟ZHD与探空数据计算的实际ZHD进行了对比，表明Saastamoinen模型计算干延迟在北极黄河站区是可靠的;

(2)对黄河站区的大气加权平均温度进行了研究，得到了适合该地区的大气加权平均温度模型，计算模型为Tm=27.678 9+0.867 8Ts;

(3)将GAMIT计算的PWV值与探空值进行比较，两者的标准差＜2 mm，达到了较高的精度。

本文GPS反演的可降水量精度优于2 mm，达到了较高的水平，这是由以下几个原因决定的:GAMIT解算时采用了每30 min估计对流层天顶延迟的策略，保证了足够的时间分辨率;基线解算结果质量高，基线重复性达到了10-9量级;所选气象站距离黄河站GPS观测站距离＜500 m，且高差相差＜40 m，无需进行高度订正即可得到符合黄河站GPS观测站的气象观测值，确保了干延迟计算结果的精度。

GPS气象技术是气象预报困难或对短期预报高要求地区的有力手段，相比于无线电探空仪和水汽微波辐射计，其具有探测时空分辨率高、全天候、近实时、成本低廉等诸多优点。由于黄河站处于北半球高纬度地区，其气候特征具有明显的代表性，利用GPS技术遥感北极黄河站可降水量是极地气象研究的有益补充，对全球气候变化研究具有重要意义。

但同时GPS气象学仍然有一些亟待解决的问题，无论是理论上还是技术上都有需要推陈出新的地方，如地基GPS与空基GPS气象学的融合问题、基于精密单点定位技术的GPS水汽反演、GPS遥感水汽在数值天气预报资料同化中的应用等等。

可以预见，在不远的将来，GPS气象技术必将在高空气象探测和天气预报技术的发展中扮演越来越重要的角色。

致谢感谢全球气候变化组织及德国Koldwey气象站(http://www.awi-bremerhaven.de/MET/NyAlesund/wettertab.html，ftp://ftp.bsrn.awi.de)提供的气象数据，感谢美国Bob King博士在GPS数据处理方面给予的指导和帮助。

1 Askne J， Nordius H.Estimation of tropospheric delay formicrowaves from surface weather data.Radio Science， 1987， 22(3):379-386.

2 Bevis M，Businger S，Herring T，et al.GPSmeteorology-Remote sensing of atmospheric water vapor using the Global Positioning System.Journal of Geophysical Research，1992，97(D14):15787-15801.

3 Rocken C，Hove T V，Johnson J，etal.GPS/STORM-GPSsensing of atmospheric water vapor formeteorology.Journal of Atmospheric and Oceanic Technology， 1995， 12(3):468-478.

4 Dick G，Gendt G，Reigber C.Operationalwater vapor estimation in a dense German network//Proceedings IGSAnalysis Center Workshop， June.1999:375-384.

5 王小亚，朱文耀，严豪健，等.地面GPS探测大气可降水量的初步结果.大气科学，1999，23(5):605-612.

6 杨红梅，何平.用GSP资料分析华南暴雨的水汽特征.气象，2002，28(5):17-21.

7 曹云昌，方宗义，李成才，等.利用GPS和云图资料监测北京地区中小尺度降水的研究.高原气象，2005，24(1):91-96.

8 Kursinski E R，Hajj G A，Schofield JT，et al.Observing Earth's atmospherewith radio occultationmeasurements using the Global Positioning System.Journal of Geophysical Research:Atmospheres(1984-2012)，1997，102(D19):23429-23465.

9 陈立奇，赵进平，卞林根，等.影响北极地区迅速变化的一些关键过程研究.极地研究，2003，15(4):283-302.

10 陆龙骅，卞林根，逯昌贵.北极边界层物理过程的考察与研究.极地研究，2004，16(3):161-192.

11 陆龙骅，卞林根，效存德，等.极地大气科学与全球变化研究进展.应用气象学报，2007，17(6):743-755.

12 陈立奇.南极和北极地区变化对全球气候变化的指示和调控作用---第四次IPCC评估报告以来一些新认知.极地研究，2013，25(1):1-6.

13 程振波，石学法，陈志华，等.2007中国北极黄河站夏季科学考察及黄河站概况.海洋科学进展，2008，26(1):112-118.

14 King RW，Bock Y.Documentation for the MITGPS analysis software:GAMIT.Mass.Inst.of Technol.，Cambridge，2004.

15 周国君，潘雄.GPS水汽遥感中加权平均温度获取方法研究.测绘与空间地理信息，2006，29(4):14-16.

16 Rocken C， Ware R， Van Hove T，et al.Sensing atmospheric water vaporwith the Global Positioning System.Geophysical Research Letters，1993，20(23):2631-2634.

17 谷晓平，王长耀，王汶.GPS水汽遥感中的大气干延迟局地订正模型研究.热带气象学报，2004，20(6):697-703.

18 李凯锋，欧阳永忠，陆秀平，等.静态精密单点定位中对流层延迟估计.海洋测绘，2011，31(6):12-15.

19 刘焱雄，陈永奇.利用地面气象观测资料确定对流层加权平均温度.武汉测绘科技大学学报，2000，25(5):400-404.

20 Duan J， Bevis M， Fang P， et al.GPSmeteorology:Direct estimation of the absolute value of precipitable water.Journal of Applied Meteorology，1996，35(6):830-838.

21 Ingold T， Peter R， Kämpfer N.Weightedmean tropospheric temperature and transmittance determination atmillimeter-wave frequencies for groundbased applications.Radio Science， 1998，33(4):905-918.

22 李建国，毛节泰，李成才，等.使用全球定位系统遥感水汽分布原理和中国东部地区加权“平均温度”的回归分析.气象学报，1999，57(3):283-292.

23 包东琴，布和，巴特儿.基于MATLAB的对流层加权平均温度模型的研究.科学技术与工程，2011，11(35):8840-8845.