超声波检测中的小波降噪
2015-01-27胡铁华靳倩倩张晓军
刘 锐,胡铁华,靳倩倩,张晓军
(1.机械科学研究总院 中机生产力促进中心,北京 100044;2.安徽星瑞齿轮传动有限公司,安徽 六安 237010)
0 引言
超声波检测(Ultrasonic Testing,UT)一般是指使超声波与工件相互作用后,对反射、透射和散射的波形进行研究,从而进行试件的宏观缺陷检测、几何特性测量、组织结构和力学性能变化的检测和表征,并进而对其特定应用性进行评价的技术。由于检测灵敏度高、方便对缺陷定位和定量等优势,这种检测方法目前已成为一种广泛应用的无损检测方法。
小波分析是一门正在迅速发展的新兴学科,目前,它在实际中得到了广泛的应用。研究小波的新理论、新方法以及新应用具有重要的理论意义和实用价值。小波之所以在信号处理领域具有很大的优势,在于小波变换可以获得信号的多分辨率描述,同时,小波变换具有丰富的小波基可以适应具有不同特性的信号。因此小波分析技术受到了广大超声信号处理领域学者的重视。
1 小波分析在检测信号处理中的应用
小波分析是根据信号和噪声的小波系数在不同尺度上具有不同性质的机理,构造相应规则,在小波域采用一定的方法对含噪信号的小波系数进行处理。处理的实质在于减小甚至完全剔除由噪声产生的系数,同时最大限度地保留有用信号的系数,最后由经过处理的小波系数重构原信号,得到真实信号的最优估计。小波降噪的过程一般由三个步骤来完成[1]:①选择一种母小波并确定小波分解层数,然后对信号进行小波变换;②对变换后的小波系数进行非线性处理,以滤除噪声;③将处理后的小波系数进行小波逆变换,重构信号。
2 超声波的传播特性
2.1 超声波传播特性的基本原理
超声波是超声频率的机械振动在弹性介质中的一种传播过程。在进行实际探伤时,金属介质则完全可以作为连续介质,因此可以把金属介质作为典型的弹性介质,而缺陷一般为气孔、裂纹等,因此,可以将超声波在金属中的传播分别看成是:当超声波遇到缺陷时,超声波是由固体中射到固体与空气的交界面上;当超声波在无缺陷的金属中传播时,则是超声波遇到了固体与固体的交界面。总而言之,不论是传到固体与空气的交界面上还是固体与固体的交界面上,都可看成是超声波在弹性介质中传播时遇到障碍物(声阻抗与周围介质不同的物体)。故在超声波传播过程中能量逐渐减弱。
超声波在介质中的传播是比较复杂的。当超声波垂直入射到两种介质的界面时,一部分能量透过界面继续传播,一部分能量则被界面反射回来,这一特性就是超声波检测缺陷的物理基础。而当超声波斜入射到两种介质的界面上时,则会产生反射、折射和波型转换现象。图1 为纵波入射到界面上的原理示意图。
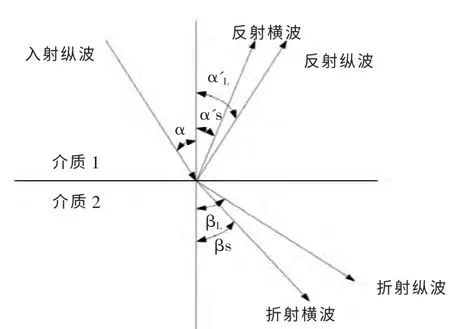
图1 纵波入射到界面上的示意图
2.2 超声回波信号中的噪声
超声检测过程遇到的噪声可分为两种,即声学噪声和非声学噪声。非声学噪声中经常讨论的是电噪声,而声学噪声主要是结构噪声。而在超声检测中,结构噪声对超声波回波信号影响较大。结构噪声是由待检材料内部的微观结构对超声入射波的散射引起的。
3 小波变换的基本原理
小波变换和傅里叶变换的出发点都是将信号表示成基函数的线性组合, 所不同的是傅里叶变换采用时间属于(-∞,+∞)的谐波函数einx作为基函数,而小波变换的基函数是基本的小波母函数Ψ(t),通过对母函数Ψ(t)进行伸缩和平移得到一个小波序列:

若a,b 不断的变化,我们可由Ψ(t)得到一族函数Ψa,b(x)。给定平方可积的信号x(t),即x(t)∈L2R,则x(t)的小波变换:

其中:Ψ*(t)—Ψ(t)的共轭函数。
4 小波降噪的方法
4.1 含噪声的超声回波数学模型
在宽带超声检测中,超声回波信号通常是一个被探头中心频率调制的宽带信号,其在T 时刻有一缺陷反射回波,可令它是一高斯包络的脉冲[2]:

式中:f0—发射超声脉冲的中心频率;A—缺陷反射回波幅度;α—决定超声缺陷回波信号的带宽,为一正常数;φ0—初相位。
而实际的超声检测回波信号则是缺陷信号、结构噪声和仪器电噪声的迭加,即:

式中:f(t)—含噪声的超声回波信号;s(t)—真实不含噪声的超声回波信号;u(t)—噪声信号(其中包括结构噪声和电噪声)。
在实际信号采集过程中,采用的是等间隔点进行数据采集的,所以将上式改写为:

对信号f(i)进行降噪的目的就是要抑制信号中的噪声部分,从而在f(i)中得到有用信号s(i)的一个逼近信号,使得其在某种误差估计下是s(i)的最优逼近。
在实际工程应用中,超声波信号常常是非平稳信号,其中有用信号常常表现为低频信号,噪声信号则表现为高频信号。但是在非平稳信号中,高频部分通常含有在检测过程中需要得到的有用信息。因此,对非平稳信号作降噪处理,不仅仅是消除噪声所表现的高频量,另外还要保留那些反映信号重要特征的高频量。用传统的方法(如傅里叶变换)不能满足非平稳信号降噪处理的要求,因为它不能区分有用高频量和属于噪声的无用高频量,它也不能给出在某个局部时间段或时间点上的信号频域是如何变化的。而小波变换(尤其是正交小波变换)具有很强的去数据相关性,在高频部分它能够使有用信号的能量集中在一些大的小波系数中,而噪声的能量却分布于整个频段内,而且噪声的方差和幅值随着小波变换尺度的增加会逐渐减小,而有用信号的方差和幅值随小波变换尺度的增加反而逐渐增大。因此,经小波变换后,信号的小波系数幅值要大于噪声的系数幅值,根据噪声和有用信号的不同小波变换特性,就可以对信号进行降噪处理。基于小波变换的信号降噪过程如图2 所示。根据该方法所得原始信号和处理后信号如图3 所示。

图2 小波降噪流程图
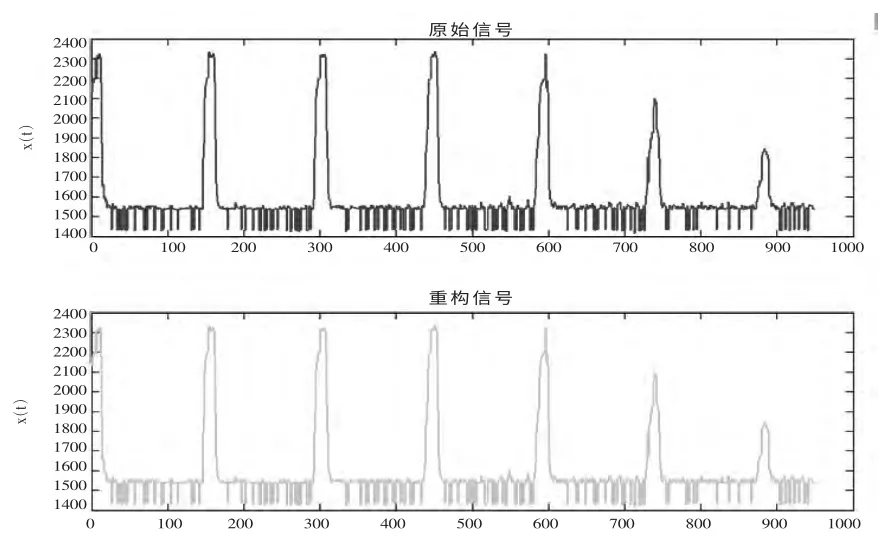
图3 基于小波分解与重构法降噪
4.2 小波变换阈值降噪
由于小波变换的小波基都是紧支集,因此小波变换具有一种“集中”的能力,可以使信号的能量在小波变换域集中于少数系数上,那么相对来说,对这些系数的取值必然大于在小波系数域内能量分散于大量小波系数的噪声的小波系数值,这就意味着对小波系数进行阈值处理可以在小波变换域中去除低于固定幅度的噪声。小波阈值降噪方法可以分为硬阈值法和软阈值法两种。
其中硬阈值的处理步骤如下[3]:①先把信号做小波变换,得到小波系数;②计算出阈值,把小波系数的绝对值与阈值进行比较,小于或等于阈值的点设为零,大于阈值的点保持不变;③再把处理过的小波系数进行小波变换来重构信号。其原始信号和处理后的信号如图4 所示。

图4 硬阈值降噪
软阈值的处理步骤如下:①含噪信号进行小波分解,选择合适的小波,确定小波的分解层数M,并对信号进行二进离散小波分解。可选用Db4 小波,可通过正确设计的QFM(正交镜像滤波器)来实现;②对信号分解后的各层系数进行适当处理:对第1 到第M 层的小波系数,选择一个软阈值(n 为信号长度),对每一层的小波系数进行阈值量化处理;③信号的重构:对量化处理后的各层小波系数进行信号的小波重构。其原始信号和处理后的信号如图5 所示。

图5 软阈值降噪
5 总结
从三种降噪的仿真结果可以看出:利用小波分解与重构法降噪,会将高频系数强制置0 后重构信号,会损失信号的部分细节,若为图象降噪会使其变得模糊,而小波阈值降噪的方法相比小波分解与重构法而言效果较好。但硬阈值降噪。把信号的绝对值与指定的阈值进行比较,小于或等于阈值的点变为零;大于阈值的点保持不变;而软阈值降噪,即把信号的绝对值与指定的阈值进行比较,小于或等于阈值的点变为0;大于阈值的点变为该点值与阈值的差。一般来说,硬阈值比软阈值处理后的信号要粗糙一些。
[1]樊启斌.小波分析[M].武汉大学出版社,2008.
[2]刘瑾. 基于小波分析的超声波信号降噪研究[D].中国石油大学,2010.
[3]周伟. 基于MATLAB 的小波分析应用[M].西安电子科技大学出版社,2010.
