剖析分数傅里叶变换及其应用

左岚

湖北省咸宁职业技术学院 （咸宁437100）

随着科学技术的发展，人们的生活水平不断提高，各种基于计算机科学技术、通信技术的产品充斥在我们的生活中，已经成为我们现代化生活的不可获取的重要部分。尤其是互联网络的快速发展，更是极大地改变了人们的生活方式以及思维方式，对于人们的生活水平来说，具有非常重要的意义。然后在这些产品的背后，是由各种数学以及物理理论基础作支撑而发展起来的。在我们的通信设施中，如何将各种低频率的语音、文字信号千里迢迢轻松地传送到千里之外，如何将各种视频、声音、图片信号如何通过互联网络方便、快捷地并且突破地域的限制来高效省时地无障碍安全传输等，这些问题的解决都是依赖于数学基本理论和物理基础技术来实现的。其中，分数傅里叶变换就是其中一个最重要的数学基础理论，通过分数傅里叶变换，实现了各种信号的时间领域和频率领域的变换，极大地简化了人们对信号的认识，从根本上改变了对信号处理的方式，使得人们通过处理信号的某些频率即可实现对传统时域信号的处理和控制。分数傅里叶变换对于互联网通信来说是非常重要的，尤其是实现互联网安全通信的数字水印加密算法上，为互联网的通信加密提供了最重要的理论依据，从而为互联网的安全可靠的通信奠定了坚实基础。

1 分数傅里叶变换简述

傅里叶变换是传统的信号分析方法，简单地理解，就是将一个信号可以拆分成多个信号的集合叠加。如果一个时域信号f(t)为时间t的周期函数，并且满足，在t的周期范围内，f(t)是连续的且处在第一类间断点的个数是可数的，则有如下公式：

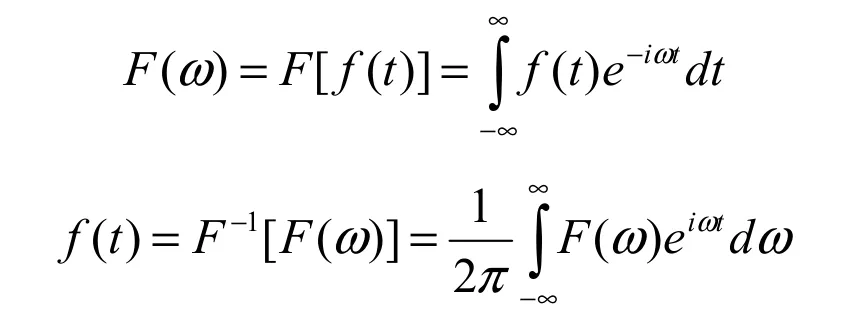
其中，f(t)为t的函数，又称为时域函数，F(ω)是该f(t)函数的频域信号表现形式，即频域函数，而上述两个公式，由时域转变成频域的称之为傅里叶变换，而频域转变成时域的则称之为傅里叶逆变换。

而分数傅里叶变换则是传统的傅里叶变换的继续和延·伸，是在分数级别上的傅里叶扩展，即现在的广义上的傅里叶变换。由上述傅里叶变换公式可知，有

其中F为傅里叶变换的表示符号。

在该，假如对f(t)信号进行多次次傅里叶变换，假如经过n次傅里叶变换，我们使用Fn来表示，则很容易得出以下公式。

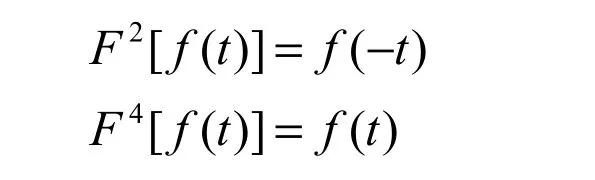
其实，每一次傅里叶变换，对于f(t)函数来说就是在坐标轴内进行一次π/2的旋转角的旋转，经过两次的傅里叶变换则有原始时域函数旋转 180°，经过四次傅里叶变换，则有原始时域函数旋转 360°，故而有上述公式。分数傅里叶变换则是在此多次傅里叶变换的基础上提出来的。在很多分数傅里叶变换中，有两种类型的分数傅里叶变换较为出名，一是 Namias型的分数傅里叶变换，一是 Shih型的分数傅里叶变换。

其中Namias型的分数傅里叶变换是对一维输入信号f(t)来说，其p阶分数傅里叶变换公式如下：

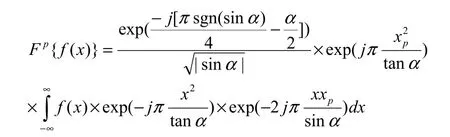
Shih型的分数傅里叶变换使用级态函数的叠加方法，表达式如下：

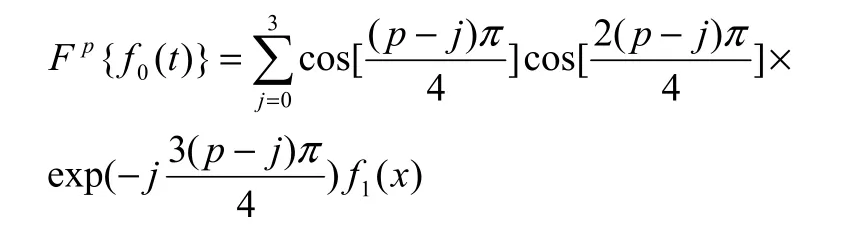
结合上述两种分数傅里叶变换，基于传统的傅里叶变换可知，分数傅里叶变换对时域和频域中表现出最基本的3个性质。

第一就是连续性，即在整个变换域中，分数傅里叶变换是连续的，无断点的。

第二就是边界性，即对于分数傅里叶变换来说，属于广义的傅里叶变换，包含了传统的傅里叶变换，也成狭义的傅里叶变换，对于某些特殊的边界，如分数阶级p为整数时，此时即为狭义的傅里叶变换。

第三是可叠加性，即对于一个分数傅里叶变换的任意分数阶级P1，P2来说，其可以任意叠加，既有

2 分数傅里叶变换的应用

现代的年代是数据泛滥的年代，尤其是在现在版权声明叫嚣的年代，更应该加强版权保护意识，对于图像、图片等直观的数据信息来说，添加数字水印是常用的一种版权保护的方式。分数傅里叶变换在互联网中的应用非常广泛，可以通过分数傅里叶变化，将互联网中的各种数据信息加上版权标识，以此来防止互联网数据被窃取商用，尤其是对于数字水印添加来说，更是方便实现。

简单地理解，数字水印就是对原有的图像、图片信息添加上版权标识，即在画面上添加该数据所属单位等版权信息。利用数字图像处理的方法，将原有的图像数据通过添加某些数据信息，使得在对原始图像显示的时候，会将添加的信息表现出来。如果该添加的数据信息就是版权标识信息，那么即可实现数字水印的添加。实际上，在原始数据上嵌入水印信息，是在原始图像的强信号上，有效地叠加一个水印数据的弱信号，如果该信号的频率幅度足够小，低于人类视觉系统的HVS对比度，那么就可实现让人类的视觉系统扑捉到，即可实现在不改变原有视觉效果的情况下为数据图像信息嵌入版权标识的数字水印。

假如原始的图像、图片数据为I，待添加的版权表示为W，为图像进行加密的数据为K，那么添加水印后的图像、图片数据表达式则为：

对于实现水印嵌入的系统结构来说，需要三部分构成，第一部分即为原始图像信号输入端，第二部分即为待添加的版权标识的数字水印信号输入端，第三部分即为图像加密的数据信号输入端。如图1.所示，为原始图像信号添加数字水印的结构示意图。如图1.的结构图所示，图像信号数字水印添加需要三个信号的输入，分别是原始图像信号 I，加密数据信号K以及水印信号W，然后通过数字水印嵌入算法即可实现数字水印的添加，最后生成添加水印的图像进行传播。

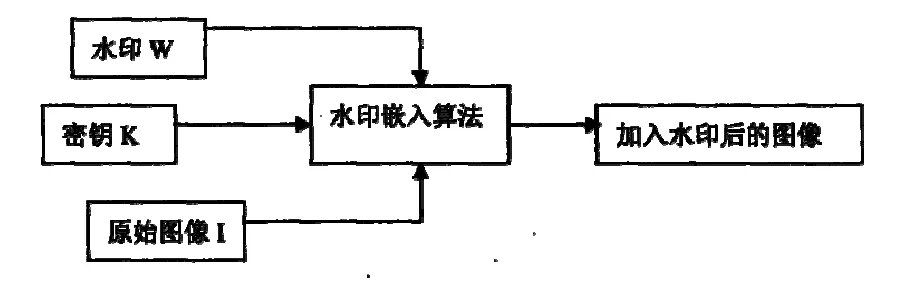
图1 原始图像信号添加数字水印系统结构示意图

在整个数字水印嵌入系统中，最重要的部分即为水印嵌入算法的实现。由于原始图像信号 I，加密数据信号K以及水印信号W均为数字信号，首先我们可以通过分数傅里叶变换将三个信号都转换成频域信号，可以利用 Namias型的分数傅里叶变换公式来实现，然后将三者的频域信号进行叠加，即可实现原始图像信号I，加密数据信号K以及水印信号W三者的频域叠加，由于在频域中，不同的信号可由多个不同频域的信号构成，而不同频域信号的强弱则表示了原始信号的主信号，并且某一个时域信号的多个不同频域信号是线性叠加的，即通过向加减即可实现，所以原始图像信号I，加密数据信号K以及水印信号W的频域信号的叠加，就是处在相同频率的信号的系数增加，最终整体表现出的现象就是在频域中不同频率的信号幅度值有所改变。所以，采用分数傅里叶变换的来实现三者信号的叠加的关键是，必须要求三者时域信号的主频率必须不能相同，转换到频域中，即叠加后的信号会在三个主要的频段中幅度出现高峰。这就为后期的图像还原奠定了基础，即通过过滤原始信号的主频段范围内的信号即可生成原始图像。这是非常容易实现了，数字水印要求的频段本来就是要求低于人类视觉系统的扑捉门限，而原始图像必须在人类视觉性对比度门限内，所以数字水印信号不会与原始图像信号的主频段冲突，至于加密数据的频率只需要区别于数字水印频段以及原始信号频段即可是实现利用分数傅里叶变换来实现互联网图像的数字水印嵌入技术。

[1]金伟民,颜才杰.变形分数傅里叶变换双随机相位加密技术[J].应用激光. 2005(06)

[2]陈寅伟. 基于分数傅里叶变换的数字水印技术[D].吉林大学.2010.

[3]文亮. 分数傅里叶变换及其应用[D].重庆大学,2008.