三相不控整流电路参数仿真与优化设计

王军伟

（太原重工股份有限公司 山西 太原 030024）

随着我国工业的发展，采用三相不控整流拓扑的变频器被广泛的应用于各行各业。变频器驱动的异步电机具备速度调节、峰值电流控制等功能。目前国内外对变频器的研究主要集中于拓扑、整流逆变、控制方式等多方面[1-4]。文献[1]对PWM整流进行了研究，并对功率因数做了相关说明，但是文中提供的采用MATLAB计算功率因数的方法过于复杂；文献[5]对不控整流的谐波做了理论分析，但是并未明确给出LC滤波器的设计选型范围。

本文首先对三相不控整流的重要性进行了分析，并采用MATLAB建立了三相不控整流的仿真模型，该仿真模型可以自动计算输入的功率因数，而且对三相不平衡等特殊情况也可以进行仿真；然后仿真分析了三相不平衡对整流器性能的影响，并指出了LC滤波器参数的最佳设计范围；最后给出结论。

1 三相不控整流的MATLAB仿真模型建立

仿真模型是基于MATLAB的Simulink建立，用到的模块主要来自SimPowerSystems库。如图1上半部分所示，从左到右依次是三相电源、三相电压电流测量模块（选择测量相电压）、二极管整流桥、LC滤波和等效负载电阻R。由于母线几乎是平稳的，所以可以用电阻R来等效负载。PF_calc是封装好的功率因数测量模块，内部拓扑如图1下半部所示。图1上方的Multimeter模块输出负载电阻上的电压和电流用于计算输出功率。

图1下半部分为功率因数测量模块内部，首先通过三相瞬时有功/无功模块和平均值模块计算出有功功率，然后通过各相的电压与电流有效值的乘积相加得到视在功率，用有功功率除以视在功率即可得到功率因数。这样设计的好处是即使三相电压不平衡，也可以通过该模块仿真出功率因数，增加了适用范围。

2 电网电压不平衡对三相不控整流性能的影响

本分析基于某品牌的37 kW变频器的三相不控整流电路参数进行分析：滤波器L=400μH，C=2 800μF，其截止频率根据公式1可得为150 Hz。

在输入三相电压平衡且电感L电流连续的前提下，二极管整流后的电压是理想的六脉波，设输入的三相电压如公式2所示，在π/6到π/2之间，该六脉波的电压表达式为sin（ωt）-sin（ωt-2π/3）。 对六脉波进行傅里叶分解如下[6]：

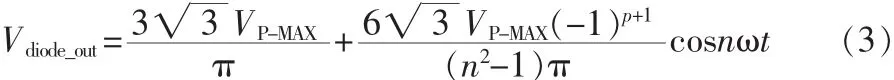
图1 MATLAB整体仿真图Fig.1 Simulation diagram of three－phase uncontrolled rectifier based on MATLAB

该六脉波的直流分量就是输出电压的平均值，根据P=U2/R可得到输出37 kW时，等效电阻R阻值为7.112Ω。通过仿真，可以得到输出电压的波形如下。

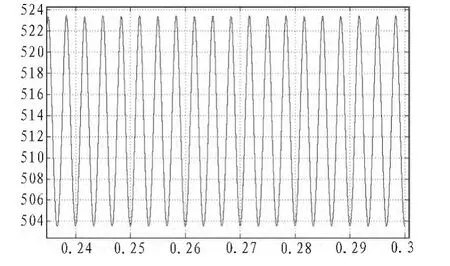
图2 负载电阻上的输出电压Fig.2 Output voltage of load R

图2 中电压的最大值和最小值分别是523 V和503.6 V，可以计算出母线波动的百分比是3.86%。通过powergui模块对电感L中电流进行傅里叶分析，可以得到其谐波成分主要是 k=6n次谐波，n=1，2，3…n＞0。 所以在设计 LC 滤波器的时候，通常设计LC滤波器的截止频率小于6次谐波对应的频率值。以输入电网频率为50 Hz计算，则LC滤波器的截止频率需小于300 Hz，并保证输出电压波动不高于5%，如果波动过大则母线电容纹波电流会过大，从而影响其寿命；此外，纹波过大会影响输出电流的波形质量。对输入的相电流进行傅里叶分析，可以得到电流主要谐波成分是k=6n±1次，n=1，2，3…n＞0。

当输入电压不平衡时，此处假设A相的输入电压只有正常值的96%，既考虑4%的电网电压不平衡，仿真结果如下：

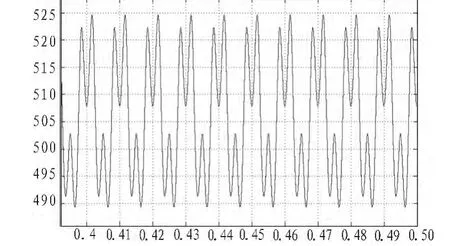
图3 三相不平衡时负载电阻上的输出电压Fig.3 Output voltage of load R under unbalanced input voltage condition

图3 中电压的最大值和最小值分别是524 V和489 V，可以计算出母线波动的百分比是6.82%。通过powergui模块对输出电压进行傅里叶分析，可以得到其谐波成分主要是k=2n 次谐波，n=1，2，3…n＞0。 所选 LC 滤波器的截止频率为150 Hz，对2次和3次谐波不能滤除，所以导致输出电压波动变大。对输入的相电流进行傅里叶分析，可以得到电流主要谐波成分是 k=2n－1 次，n=1，2，3…n＞0。 对输入电流谐波失真 （THDI）进行分析，可得A相 THDI是63.74%，B相是68.51%，C相是51.38%。

当A相出现4%不平衡过压时，即A相输入电压为额定值的104%，输出电压的最大值和最小值分别是544 V和499 V，波动百分比是8.77%。，对输入电流进行THDI分析，可得A相THDI是60.60%，B相是53.61%，C相是69.31%。

从图4可以看出，一旦有一相电压达到不平衡，输出电压都会出现波动，并且在电网某一相电压偏大时更严重，波动范围比正常值高出一倍。而三相电流各自的THDI在电网不平衡条件下也发生变化，如果某一相电压变低 （例如A相），则相位滞后该相的相（B相）THDI会变高，相位超前该相的相（C相）THDI会变低，如果某一相电压变高则结果正好相反。

图4 各种条件下输出电压波动范围Fig.4 Range of output voltage and THDI under different conditions

从硬件角度解决不平衡条件下的母线电压波动，理论分析上可以通过设计截止频率更低的LC滤波器实现。但实际上，增大L或者C后，LC滤波器的截止频率确实会降低，但此时电感L电流已经不连续，二极管整流后输出的波形也就不是固定的6脉波波形，加大L或者C后反而可能使输出电压波动更大，下面通过仿真来分析。

如果保持C=2 800μF不变并使截止频率降低到100 Hz，通过公式1计算可得L要增大到900μH，如果保持L=400μF不变并使截止频率降低到100 Hz，计算可得C要增大到6 300μH。当A相电压不平衡时，仿真结果如下：

表1 A相输入电压为96%额定电压仿真结果Tab.1 Simulation result under input voltage of phase A is 96%rated voltage

从表1可以看出，加大L或C反而使输出电压的波动变大了。因为LC滤波器的波特图中，存在增益大于1的情况，如图7所示。所以LC滤波器的设计并不是越大越好，通常设计LC滤波器的截止频率大约为电网频率的3～4倍。

3 结 论

本文建立了基于MATLAB的三相不控整流电路的仿真模型，该模型可以自动计算出输入的功率因数，并且能仿真出电网不平衡等特殊条件下的功率因数。此外本文对电网不平衡对三相不控整流电路的影响做了深入研究，并指出通过降低LC滤波器的截止频率来降低电网电压不平衡条件下母线波动是不合适的，而且这样设计的LC滤波器成本也会增加，通常LC滤波器截止频率的最佳的范围在电网频率的3至4倍。

图5 L=900μH C=2 800μF R=7.112Ω条件下的波特响应图Fig.5 Bode response plot under L=900μH C=2 800μF R=7.112Ω

[1]马宁丽，王航宇.基于MATLAB的高功率因数整流器仿真实验平台研究[J].电子设计工程，2009，17（2）:59－61.MA Ning-li，WANG Hang-yu.Research of high-power-factor rectifier simulating experiment platformbased on MATLAB[J].Electronic Design Engineering，2009，17（2）:59－61.

[2]崔晶.高性能V/f控制在中压变频器中的实现[J].电子设计工程，2009，17（6）:120－122.CUI Jing.Realization of high performance V/f control modularization in mid-voltage inverter[J].Electronic Design Engineering，2009，17（6）:120－122.

[3]叶和忠，刘倍圣，曾亚军，等.一种正交数字下变频器的高效改进结构[J].电子设计工程，2010，18（9）:186－189.YE He-zhong，LIU Bei-sheng，ZENG Ya-jun，et al.An efficiently improved structure for quadrature digital down converter[J].Electronic Design Engineering，2010，18 （9）:186-189.

[4]田力，高明，任蔚.级联型变频器在高压大功率电机软启动中的应用[J].电子设计工程，2013，21（15）:31-33.TIAN Li，GAO Ming，REN Wei.Cascade inverter used in high-voltage high-power motor soft-start[J].Electronic Design Engineering，2013，21（15）:31-33.

[5]裴云庆，姜桂宾，王兆安.LC滤波的三相桥式整流电路网侧谐波分析[J].电力电子技术，2003，37（3）:34-36.PEIYun-qing，JIANG Gui-bin，WANG Zhao-an.Analysis of line harmonic current of three-phase rectifier with LCfilter[J].Power Electronics，2003，37（3）:34-36.

[6]Sakui M，Fujita H，Shioya M.A method for calculating harmonic currents of a three-phase bridge uncontrolled rectifier with DC filter[J].Industrial Electronics，IEEE Transactions on，1989，36（3）:434-440.