一种用于深空通信的系统LT码
2015-01-25王丽娜胡广大
王丽娜,魏 鹏,胡广大,唐 伟
(1.北京科技大学计算机与通信工程学院,北京100083;2.北京科技大学自动化学院,北京100083)
0 引言
深空通信具有传播距离遥远、传播延时长、误码率高、传输链路易中断等特点,而且航天器的存储容量和处理能力又很有限,因此采用传统的前向纠错技术不能有效地保证信息传输的可靠性[1]。喷泉码是一种无码率、无需反馈链路的前向纠错码,可以在不需要反馈信道的情况下高效地恢复数据,避免了反馈重传机制应用于深空通信时的瓶颈问题。喷泉码的编译码复杂度较低,将其应用于深空通信时可以降低航天器的编译码时间,缓解深空通信长延时带来的不利影响,而且不存在反馈拥塞问题[2-5]。喷泉码还具有恢复闪断数据的能力,可以有效改善接收信号起伏大、甚至闪断等问题[6]。
LT(Luby Transform)码[7-8]是第一类实用的喷泉码,是针对删除信道提出来的一种纠错码。LT码的编码思想是根据编码器的有限输入与无限输出的映射特性生成数据包,当接收端收到一定数量的数据包时就可以恢复出原始信息,以此来保证信息传输的可靠性。深空通信信道与无记忆的加性高斯白噪声(AWGN)信道非常相似,可以建模为理想的AWGN信道。由于LT码是一种以删除信道为背景的稀疏图编码,当其应用于深空通信时存在一定的译码失败概率,而且LT码需要接收足够多的数据分组后才能开始译码,且会产生译码开销,这些对于功率和存储空间受限的深空通信系统来说是非常不利的。目前,已有文献对AWGN信道上LT码的性能进行研究,并提出了相应的改善措施[9-11]。本文通过对AWGN深空通信环境中LT码的研究发现,当LT码用于深空通信时,其译码性能并不理想,而且输入符号不能保证被全选。针对存在的问题,本文通过修改LT码的二分图构造系统LT码,提出一种去环的左正则LT码编码方案,这样LT码译码器可以采用置信传播(BP)译码算法[12],且能保证译码算法的有效性。本文通过采用外信息转移图(EXIT图)[13]和MATLAB仿真工具对系统LT码的性能进行分析,结果表明,提出的编码方案能够明显降低LT码的错误平层,提高BP译码算法的性能。
1 系统LT码
当传统LT码的编码符号通过AWGN深空通信信道被接收以后,译码器采用对数域BP译码算法进行译码时,传统LT码具有较高的误码率和错误平层。造成这种结果的原因有两个:一是缺少一个合适的校验矩阵;二是输入符号没有通过信道,从而缺少输入符号的初始先验概率。因此,需要依据深空通信的特性来改善LT码的性能。
1.1二分图
为了让k个输入符号s=[s1,s2,…,si,…,sk]拥有它们的先验概率p(si),需要让它们通过信道,这样就自然形成一种系统的LT码。同时,通过传统LT码的异或运算操作继续构建出二分图中校验节点和变量节点的关系。
传统LT码在删除信道下的二分图如图1(a)所示,它由输入符号和编码符号构成。为了使LT码适用于AWGN深空通信信道,本文对传统LT码的二分图进行修改,如图1(b)所示,此LT码为系统码,由变量节点和校验节点构成。
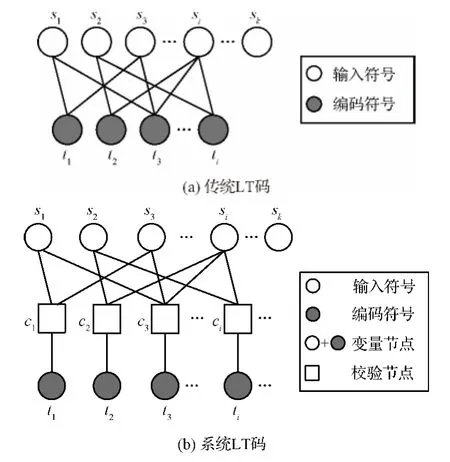
图1 LT码二分图Fig.1 The bipartite graph of LT codes
在图1(b)给出的系统LT码二分图中,输入符号s=[s1,s2,…,si,…,sk]和编码符号t=[t1,t2,…,ti,…]可以当作变量节点,c=[c1,c2,…,ci,…]与LDPC码中的校验节点类似。图1所示的系统LT码二分图与LDGM(Low-density Generator Matrix)码二分图的区别是修改后的LT码的译码开销仍然在一定的范围内,能够动态地增加编码符号的数量,保留了喷泉码无码率的特性,如同在删除信道下一样,而LDGM码的码率则是依据预估的信道模型进行固定的。二者更明显的区别是,LDGM码在编译码过程中首先要确定的是校验矩阵,该矩阵对编码器和译码器都是确定和已知的,编码时需要把校验矩阵变换成合适的分块矩阵,然后再进行编码。而系统LT码无需提前确定一个校验矩阵,它是在编码过程由无码率特性自然形成生成矩阵Gp,然后再把这个矩阵变换成合适的校验矩阵,使其构成了校验关系,最后依据这个校验关系执行BP译码算法。
LT码在二进制删除信道下遇到的一个问题是在译码开销较低时,不是所有的输入符号都被选择进入编码过程,这样就会使后续的译码一定会失败,通常需要N=k ln(k/δ)个编码符号才能保证能以1-δ的概率成功译码,其中,k为数据包的长度,δ为译码失败概率门限。同样地,在深空通信信道下,这个问题也会导致BP译码算法的性能下降。因此,可以假设所有的输入符号不是按照随机方式被选择参与编码的,而是依据它们的度数进行排序,然后优先选择度数低的符号参与编码,以期达到所有的输入符号都被选择参与编码过程,这样就提高了BP译码算法的译码性能。另一方面,删除信道下LT码的成功译码过度依赖度为1的编码符号,它们是译码过程进行下去的关键。然而,在AWGN深空通信信道环境下,度为1的编码符号并没有在BP译码算法中提供任何有益的作用。相反地,它们使得信噪比(SNR)和误码率(BER)曲线中具有较高的错误平层,因此需要修改校验节点的度分布,降低度为1的编码符号出现的概率或者不出现。
1.2编码算法
随着系统LT码编码的进行,生成矩阵Gp被逐步生成出来。如果所有的输入符号都按照相同的概率被选择,那么在生成矩阵中四环和六环的形成就难以避免,这些环会降低BP译码算法的性能[14]。为了解决这一问题,本文在文献[10]的基础上提出一种去四环和六环的编码算法。
令Ωc(x)表示校验节点的度分布,且

式中:ωi是度为i的校验节点的概率。
尽管LT码在理论上是无码率的,但在实际应用时仍需设置输入符号的最大编码符号数量n。本文提出的系统LT码编码算法步骤如下:
步骤1.接收编码符号,依据度分布Ωc(x)为第i个编码符号生成度数di,若存在没有选中过的输入符号,则进入步骤2;否则进入步骤3;
步骤2.依据每个输入符号被选择的次数对其进行排序,随机选择di个从未被选中过的输入符号,进入步骤7;
步骤3.重新把所有的输入符号加入到待选集合V中,对于第j个选择的输入符号,若j≤di,则进入步骤4;否则返回步骤1;
步骤4.从V中那些选择次数最小的输入符号里随机选择一个作为第j个输入符号,并将其从V中去除,进入步骤5;
步骤5.消除潜在的四环。把那些已存在的校验节点(即第1个到第j-1个选择的输入符号的邻居节点)作为集合P,把P中校验节点的邻居节点作为集合Q,从V中去除Q的元素,进入步骤6;
步骤6.消除潜在的六环。把P—中校验节点作为集合U,并从V中去除那些与U中校验节点相邻的节点的输入符号,返回步骤3;
步骤7.计算di个输入符号的模二加之和,并将其作为第i个编码符号,返回步骤1。
根据上述系统LT码的编码算法可以得到一个维度是k×n的稀疏矩阵Gp,则生成矩阵为G=[I Gp],其中I是一个维度为k×k单位矩阵。
编码过程可以表示为u=sG=[s t],编码符号为u=[u1,u2,…,ui,…,uk+n]=[s t],则码率为R=k/(k+n),系统LT码的译码开销为γ=n/k。

式中 为变量节点的平均度 为校验节点的平均度。
变量节点的平均度可表示为
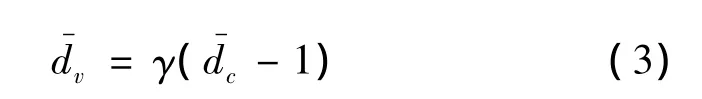
为了保证所有的输入符号都被选择,γ需要满足如下条件,即

2 系统LT码分析
2.1右正则系统LT码
考虑校验节点的度dc为常数的系统LT码,与LDPC码类似,定义这类码为右正则系统LT码。
首先采用EXIT图来分析系统LT码的收敛阈值,以说明上节提出的系统LT码编码算法既不会对校验节点的度产生影响,也不会降低LT码的性能。
变量节点被当作变量节点译码器(VND),校验节点被当作校验节点译码器(CND)[15]。对于变量节点译码器而言,输出的外信息为

相应地,对于校验节点译码器,输出的外信息为

式中:

对于右正则系统LT码,考虑校验节点的度dc分别为7、10和13的情况,译码开销γ为1.1,码率R为0.476,通过EXIT图来推断右正则系统LT码的收敛阈值,其结果如图2所示。

图2 VND和CND的EXIT图Fig.2 The EXIT charts of VND and CND
由图2可知,校验节点的度dc分别取7、10和13时,VND和CND相交的点对应的SNR分别为-0.1 dB、1.1 dB和1.9 dB。
接下来,依据第1节提出的系统LT码编码算法,通过MATLAB仿真对右正则系统LT码的译码性能进行分析。这里输入符号的数量k取1000,对数域BP译码算法的最大迭代次数设置为50。译码开销γ为1.1,码率R为0.476,当校验节点的度dc分别取5、7、9、11和13时系统LT码与传统LT码的仿真结果如图3所示。

图3 不同度分布下右正则系统LT码与传统LT码的比较Fig.3 Comparisons between right-regular systematic LT codes and conventional LT codes for different degree distribution
由图3可以看出,与传统LT码编码算法相比,本文提出的系统LT码编码算法具有更低的BER和更好的译码性能。更重要的是,提出的系统LT码编码算法能够把错误平层降低1个数量级左右,而且在陡降区下降得更快,这说明本文提出的系统LT码编码算法明显增强了BP译码算法的译码性能。从图中还可以看到,传统LT码编码算法对应的BER-SNR曲线的错误平层随校验节点度数的增加而下降,提出的系统LT码编码算法也遵循了相同的规律。此外,当SNR大于4 dB,校验节点的度dc为11和13时的系统LT码,仿真中没有发现任何的误码。当SNR低于3 dB时,校验节点度dc为7时的右正则系统LT码的性能较好。对于SNR大于3 dB,BER小于10-5的情况,校验节点度dc为9时的右正则系统LT码的性能最好。
下面对不同译码开销γ下系统LT码的BER性能进行分析。考虑校验节点的度dc∈[7,10](dc取整数)的情况,码率R为0.435,当译码开销γ分别为1.1和1.3时的仿真结果如图4和图5所示。
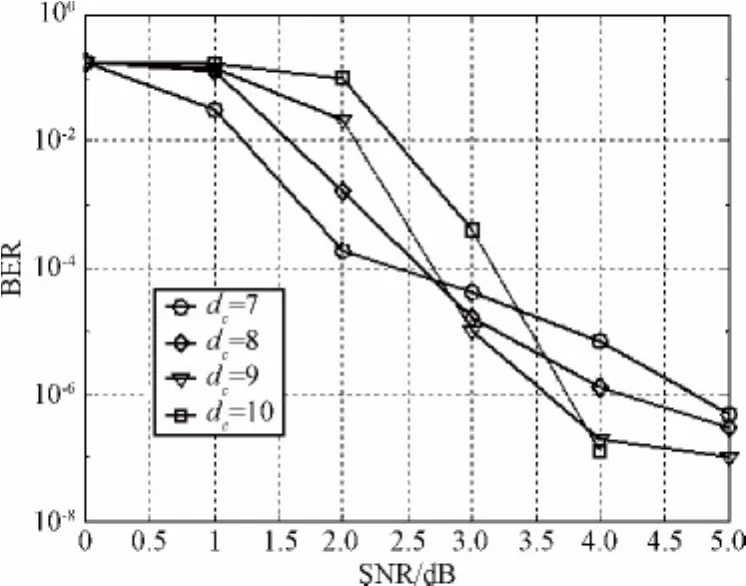
图4 γ为1.1时右正则系统LT码的BER性能Fig.4 BER performance of right-regular systematic LT codes withγ=1.1
从图4和图5可以看出,对于相同度数的右正则系统LT码,当译码开销γ分别为1.1和1.3时,其BER-SNR曲线的发展趋势类似,BER曲线在陡降区下降得较快。而且对于校验节点的度dc为9和10时的LT码,其错误平层下降得更快,同时,错误平层的斜率增大。当SNR低于2.6 dB时,校验节点度dc为7时的右正则系统LT码的性能较好。对于SNR大于2.6 dB,BER小于10-5的情况,校验节点度dc为9时的右正则系统LT码的性能最好。
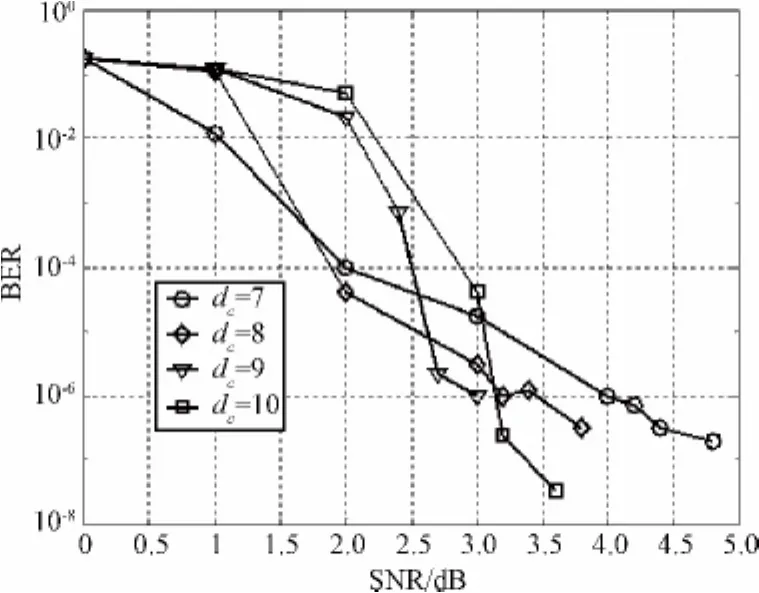
图5 γ为1.3时右正则系统LT码的BER性能Fig.5 BER performance of right-regular systematic LT codes withγ=1.3
根据图3至图5显示的结果和分析可以得到校验节点的度dc分别为7、10和13时的收敛阈值,即0 dB、1 dB和2 dB,该结果与用EXIT图分析得到的收敛阈值基本相符,说明本文提出的编码算法是合理的。对于采用本文提出的编码算法的右正则系统LT码,从整体性能上来说,当SNR低于3 dB时,采用校验节点度dc为7时的右正则系统LT码较好;而当SNR高于3 dB时,采用校验节点度dc为9时的右正则系统LT码较好。
2.2非右正则系统LT码
本节对采用提出的编码算法的非右正则系统LT码的译码性能进行分析。
依据校验节点的度dc为9时的系统LT码,根据二次拟合曲线,对i=4,5,…,12,有
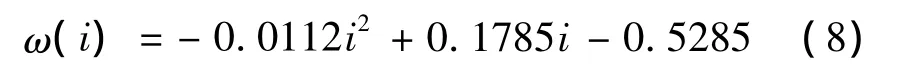

根据文献[9]和[16],针对提出的系统LT码编码算法,修改度分布来消除环,提出第二种校验节点的度分布,即


第三种度分布为

在译码开销γ为1.1,其他参数保持不变时,根据式(9)~(11)给出的三种不同的度分布,对传统LT码编码算法和提出的系统LT码编码算法的性能进行比较,其结果如图6所示。
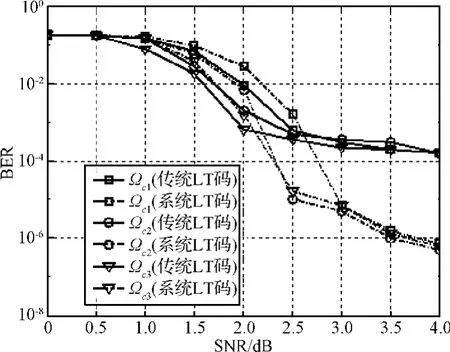
图6 不同度分布下非右正则系统LT码与传统LT码的比较Fig.6 Comparisons between right-irregular systematic LT codes and conventional LT codes for different degree distribution
从图6可以看出,在上述三种不同度分布下,本文提出的编码算法与传统LT码编码算法相比能够明显降低曲线上的错误平层,减少错误平层的斜率。因此,本文提出的编码算法能够增强BP译码算法的译码性能。
对于式(9)至式(11)给出的三种不同的度分布,非右正则系统LT码的译码性能基本相同,但是在曲线的陡降区,非右正则系统LT码的性能却不同。对于第一种度分布来说,其性能和度为9的右正则系统LT码的性能基本相同。对于第二种度分布来说,其性能在陡降区和错误平层之间有一个很好的折衷。当SNR小于2.5 dB时,采用第二种度分布的非右正则系统LT码的性能较好。当SNR为2.5 dB时,对应的BER约为10-5。对于采用第三种度分布的非右正则系统LT码,当SNR大于2.5 dB时,其性能是最优的,BER小于10-5。
选取式(10)给出的第二种度分布,对不同SNR(即r=1 dB,2 dB,3 dB,4 dB)条件下、不同码率时的非右正则系统LT码的性能进行评估,仿真结果如图7所示。
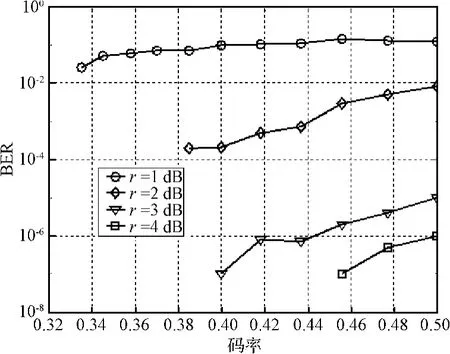
图7 不同SNR和码率下非右正则系统LT码的BER性能Fig.7 BER performance of right-irregular systematic LT codes for different SNR and code rates
由图7可以看出,非右正则系统LT码的BER随着码率的降低而减小,对于不同SNR情况下的所有非右正则系统LT码的BER性能均遵循相同的规则。当码率相同时,SNR越高,非右正则系统LT码的BER越低。从整体性能上看,SNR为3 dB时的非右正则系统LT码具有最好的BER性能,它与SNR为1 dB时的非右正则系统LT码的BER相比,大约能降低5个数量级。
从前面的分析可知,本文提出的系统LT码能较好地适应AWGN深空通信环境,具有较好的BER性能和译码性能。但由于该系统LT码在编码时要求所有的输入符号都被选择参与编码过程,故其计算复杂度要稍高于传统LT码。图8给出的是系统LT码和传统LT码分别仿真100次得到的平均编译码时间对比结果,与传统LT码相比,系统LT码需要的编码时间略长,但在可接受的范围内,不影响系统LT码的整体性能。
3 结论
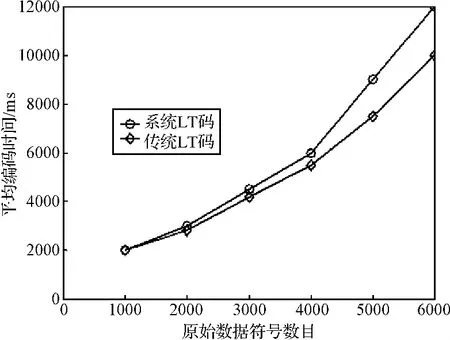
图8 系统LT码和传统LT码平均编码时间对比图Fig.8 Comparison chart of average encoding time of systematic LT codes and traditional LT codes
喷泉码以其自身独有的特点使其应用于深空通信时具有明显的优势,且发展空间非常广阔。本文针对AWGN深空通信环境中传统LT码在运用对数域BP算法时的不理想且所有输入符号不能保证被全选的问题,设计适用于此环境下的系统LT码,提出一种去环的左正则编码方案,对采用该编码方案的右正则系统LT码和非右正则系统LT码的性能进行分析,通过仿真证明了本文提出的系统LT码编码算法的有效性,并根据仿真结果说明了采用不同度分布的系统LT码的适用场合。
[1] 翟政安,罗伦,时信华.深空通信信道编译码技术研究[J].飞行器测控学报,2005,24(3):1-5.[Zhai Zheng-an,Luo Lun,Shi Xin-hua.Research on channel encoding and decoding technologies for deep space communication[J].Journal of Spacecraft TT&C Technology,2005,24(3):1-5.]
[2]Byers J W,Luby M,Mitzenmacher M.A digital fountain approach to asynchronous reliable multicast[J].IEEE Journal on Selected Areas in Communications,2002,20(8):1528-1540.
[3] 焦健,张钦宇,李安国.面向深空通信的喷泉编码设计[J].宇航学报,2010,31(4):1156-1161.[Jiao Jian,Zhang Qinyu,Li An-guo.A method of concatenated fountain codes in deep space communication[J].Journal of Astronautics,2010,31(4):1156-1161.]
[4] 顾术实,张钦宇,焦健.一种适用于深空通信的有限随机性喷泉码算法[J].宇航学报,2011,32(12):2545-2549.[Gu Shu-shi,Zhang Qin-yu,Jiao Jian.A novel algorithm of the limited-randomness fountain codes in deep space communication[J].Journal of Astronautics,2011,32(12):2545-2549.]
[5] 李云鹤,顾术实,焦健,等.面向火星临近空间的分布式中继纠删编码机制研究[J].宇航学报,2013,34(7):963-970.[Li Yun-he,Gu Shu-shi,Jiao Jian,et al.Research on distributed relay erasure codes in Mars proximity network[J].Journal of Astronautics,2013,34(7):963-970.]
[6] 吴伟仁,林一,节德刚,等.喷泉码的遥测抗闪断技术应用研究[J].宇航学报,2013,34(1):86-91.[Wu Wei-ren,Lin Yi,Jie De-gang,et al.Application of fountain coding in telemetry system[J].Journal of Astronautics,2013,34(1):86-91.]
[7]Luby M.LT codes[C].The 43rd Annual IEEE Symposium on Foundations of Computer Science,Vancouver,BC,Canada,November 16-19,2002.
[8]MacKay D J C.Fountain codes[J].IEE Proceedings Communications Online,2005,152(6):1062-1068.
[9]Hussain I,Xiao M,Rasmussen L K.LTcoded MSK over AWGN channels[C].The 6th International Symposium on Turbo Codes and Iterative Information Processing(ISTC),Brest,France,September 6-10,2010.
[10]Hussain I,Xiao M,Rasmussen L K.Error floor analysis of LT codes over the additive white Gaussian noise channel[C].2011 IEEE Global Telecommunications Conference(GLOBECOM 2011),Houston,Texas,USA,December 5-9,2011.
[11]Jesper H S,Toshiaki K,Philip O.Ripple design of LT codes for AWGN channel[C].2012 IEEE Symposium on Information Theory(ISIT),Cambridge,USA,July 1-6,2012.
[12]Yuan X,Li P.On systematic LT codes[J].IEEE Communications Letters,2008,12(9):681-683.
[13]Brink S T.Convergence behavior of iteratively decoded parallel concatenated codes[J].IEEE Transactions on Communications,2001,49(10):1727-1737.
[14]Frank R K,Brendan J F,Loeliger H.Factor graphs and the sum-product algorithm[J].IEEE Transaction on Information Theory,2001,47(2):498-519.
[15]Brink ST,Kramer G,Ashikhmin A.Design of low-density parity-check codes for modulation and detection[J].IEEE Transactions on Communications,2004,52(4):670-678.
[16]Estasmi O,Shokrollahi A.Raptor codes on binary memoryless symmetric channels[J].IEEE Transactions on Information Theory,2006,52(5):2033-2051.
