一种基于相干叠加的复合载波导航信号捕获方法
2015-01-25罗瑞丹
罗瑞丹,徐 颖,袁 洪
(1.中国科学院大学,北京100049;2.中国科学院光电研究院导航技术研究室,北京100094)
0 引言
卫星导航信号体制是决定卫星导航系统及其增强系统性能的要素之一[1],目前,各大卫星导航系统(Global Navigation Satellite System,GNSS)的信号体制设计已基本固定,而不同的卫星导航增强系统由于各自所面对的应用场景不同,其增强信号体制仍有很大的研究空间。与现代通信系统结合,利用通信系统的基础资源,将通信信号与导航测距信号进行复合设计,是导航信号体制设计未来可能的重要发展方向之一[2-3]。
在通信系统中,OFDM信号体制已经被普遍应用,OFDM信号具有多子载波的结构特征[4]。考虑到导航与通信融合是未来卫星导航增强系统发展的重要方向之一,在保持OFDM通信信号基本架构不变的前提下,在多子载波上协同发播导航测距信号有其特殊的研究价值。
目前,多载波信号已作为未来导航及增强信号的备 选 信 号,诸 如:FMT[5-6],OFDM[7],TCOFDM[8]等。我们提出了一种新的导航信号体制,称之为“复合载波导航信号体制”,并从宏观上对其架构、应用策略进行了研究[9]。结果表明,该信号体制是初步可行的,并在抗多径、抗窄带干扰,以及兼容性等方面凸显优势。
捕获是接收处理导航信号的重要环节之一,其目的是获取导航信号概略载波多普勒频移和伪随机码相位。鉴于复合载波导航信号多载波结构特征,传统捕获算法单一通道单一载波捕获的方式显然不具适用性。然而,若对复合载波导航信号各子载波信号采用传统捕获算法单独捕获,势必成倍增加运算量和硬件资源消耗。
本文对复合载波导航信号的捕获方法架构及其性能进行研究,以期支撑该新型信号体制研究的深入发展。以下首先简单介绍复合载波信号体制,然后在现有典型卫星导航信号捕获方法的基础上,提出针对复合载波导航信号的捕获方法,并分析其资源占用需求,接着对上述方法的性能进行仿真,最后进行讨论并给出结论。
1 复合载波导航信号基本结构
复合载波导航信号具有类似于通信系统的OFDM信号的结构[10],有别于OFDM信号以承载高速率通信信息为目的[11],复合载波导航信号主要用于信号发射端与接收端之间的载波相位伪距和扩频码伪距的测量,同时也用于传输低速率的导航电文(如:发射站位置、差分信息、时间信息、导航信号参数配置等)。对于第i个信号发射端,复合载波导航信号的通用表达式可写为:
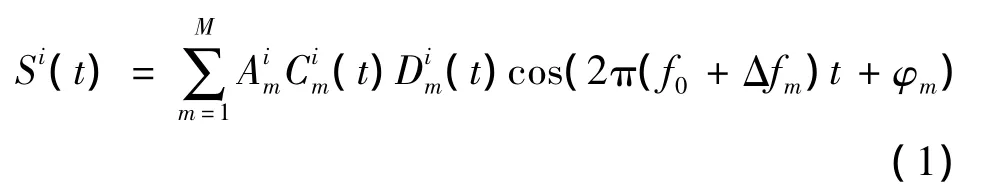
式中:M为子载波数目;m∈[1,M]为子载波编号;Am表示第m个子载波信号的幅度;Cm表示第m个子载波上调制的伪随机码,不同信号发射端采用不同的伪随机码,以BPSK的方式调制在各子载波上,以便于对不同发射端信号进行码分隔离;不同子载波可以采用不同的扩频码,以保证不同子载波间信号的正交性;Dm表示第m个子载波上调制的导航数据;f0表示起始频率,Δfm为第m个子载波频率与起始频率间的频率偏置,φm为第m个子载波信号的载波初相,不同发射端所发射信号的起始频率、各子载波与起始频率间的频率偏置相同,以便于简化接收端的软硬件设计。在子载波频率偏置量的选取上,偏置量应该大于接收信号的最大可能多普勒频移与接收机时钟频率偏差的和,以避免在信号捕获和跟踪时对信号频率的错误锁定。假设接收机与卫星相对速度引起的最大可能多普勒频移为±50 kHz,接收机本振误差引起的最大可能射频频率偏差为±20 kHz,则子载波频偏应该至少大于2×(50+20)=140 kHz。
从频域看,典型的复合载波导航信号(各子载波功率取相同值)频谱示意图,如图1所示,图中同时给出了L1频段C/A码、BOC(10,5)及P码的频谱图。由图可见,复合载波导航信号对频谱的占用更加充分,信号带外衰减更加明显。通过改变各子载波的功率,可以更加有效地回避带内窄带干扰。同时,各子载波信号可以单独跟踪,强化了对导航信号利用的灵活性。

图1 等功率复合载波信号、C/A码、P码、BOC(10,5)频谱图Fig.1 Power spectrum of NSCC,C/A,P,BOC(10,5)with equal power
通过配置式(1)中的各个参数,可结合具体的应用场景,对复合载波导航信号进行优化设计。这些参数包括:子载波个数M、各子载波强度、频率间隔Δfm、所调制伪码,以及导航电文等。因此,复合载波导航信号具有结构灵活,适应多种应用场景的特点。
在式(1)中,对不同信号发射端采用了不同的扩频码以进行码分多址隔离,从而避免不同信号发射端互相之间的干扰,同时同一信号发射端发射的不同子载波信号采用了不同的扩频码进行码分隔离。实际上,式(1)中不同子载波信号具有不同的频率偏置,本质上等效为一种频分隔离的设计,因此,不同子载波可以采用完全相同的扩频码Ci(t),为简化接收端软硬件设计复杂度打下基础,即:
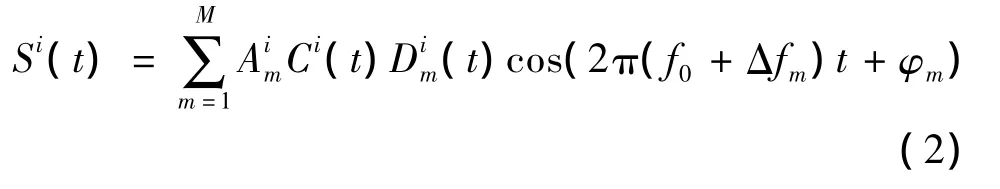
在实际设计中,可在可用频段内优化设计Δfm,m∈[1,M],保证不同子载波信号间的正交性,降低子载波信号间的互扰。
2 复合载波导航信号捕获方法
2.1捕获方法框架设计
复合载波导航信号中的每一个子载波信号从本质上讲是独立的,因此可以借用在GPS系统中已经行之有效的捕获方法架构作为复合载波导航信号捕获架构的基础。GPS信号捕获方法大致可以分为两类:一类是基于相关器在由多普勒频移和码时延组成的二维平面中进行逐点搜索的方法[12];另一类是利用FFT[13-16]的快速运算特点进行的快速捕获方法。第二类方法又可进一步分为时域并行处理、频域并行处理,以及时频域并行处理三类。从原则上讲,上述四种方法对式(1)和式(2)所描述的复合载波导航信号都适用,直接而简单的处理方式是,首先对每一个子载波导航信号按照既有方法进行逐子载波搜索,然后按照各子载波频率偏置和信号强度进行累加判决。但这样会带来计算量按子载波数目成倍增加,显然是不可取的,特别是在多普勒与码时延二维平面上逐点搜索方法,由于其本身的运算量就很大,显然不适于移植到复合载波导航信号的捕获当中。
鉴于复合载波导航信号可以被看作是同一频谱特征的子载波信号在频域上进行移位叠加而成,因此,基于FFT的频域搜索方法更加适合于复合载波导航信号的捕获。
对于式(1)所示的复合载波导航信号,可采用如图2所示的捕获算法框架。
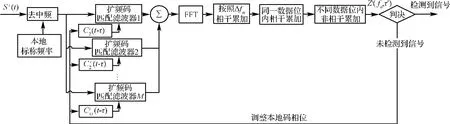
图2 复合载波导航信号通用捕获架构图Fig.2 Common framework of acquisition for NSCC
图2所示的捕获算法框架与传统的FFT频域捕获算法相比有两点区别:第一点区别是对不同子载波信号分别进行FFT处理,相关运算量增加了M倍,可能造成沉重的运算负担;第二点区别是增加了各子载波信号FFT处理结果的相干叠加环节,这一区别带来的运算量区别不大。总体上看,随着FPGA和DSP处理能力的提高,上述捕获策略有其进一步发展的可能。
对于式(2)所示的复合载波导航信号结构,由于各子载波间采用了相同的扩频码,因此,在图2的基础上,捕获架构可以大大简化,如图3所示。
与传统的单载波BPSK导航信号捕获框架相比,图3所示的框架仅增加了移位累加环节,总体上,不会明显带来运算负担和资源占用量的急剧增加。
2.2捕获方法数学模型
对于式(1)所示的发射端所发射的导航信号,接收端接收的信号可表达为:
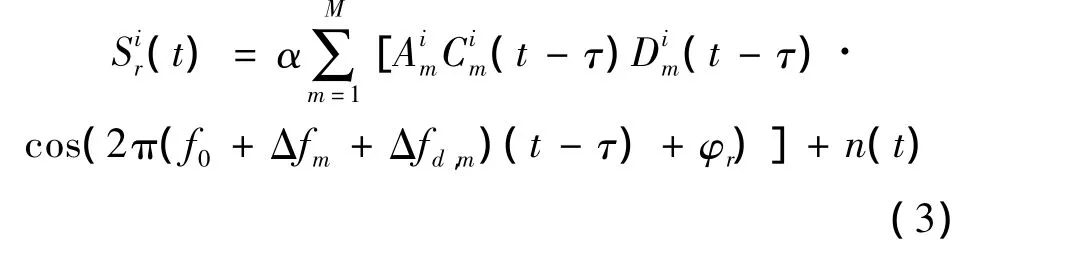

图3 复合载波导航信号简化捕获架构图Fig.3 Simplify framework of acquisition for NSCC
式中:α为信号强度的总体变化系数,τ为信号时延,φr为接收信号初相,n(t)为加性高斯白噪声。Δfd,m为第m个子载波对应的多普勒频移。考虑到同一频段导航信号的带宽一般在20 MHz以内,在这一带宽内不同的子载波对应多普勒频率频存在差异,对于L波段且信号收发端相对速度小于4 km/s时,不同子载波间的多普勒频率最大相差在250 Hz以内。
为推导方便,可忽略式(3)中α的影响,式(3)可改写为:

式中:

在图2中,经过去起始频率环节后的信号可表达为:
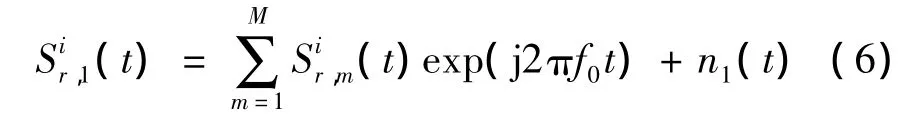
式中:n1(t)为n(t)经过上述处理环节之后的噪声。
经过扩频码匹配滤波环节后,第m'路子载波经过匹配滤波器后所对应结果的信号可表达为:
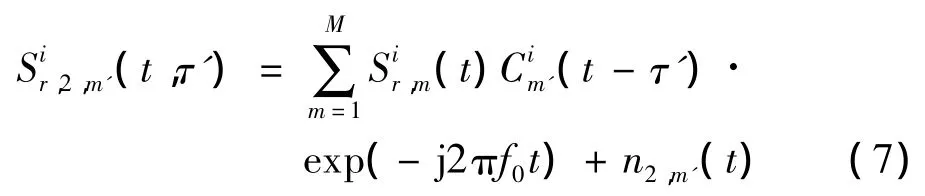
式中:n2,m'(t)为n1(t)经过上述处理环节之后的噪声。
FFT等环节后,第m'路子载波经过匹配滤波器后所对应的频谱为:
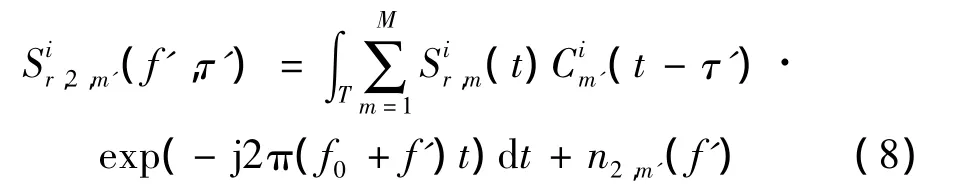
式中:n2,m'(f')为n2,m'(t)在频率域的表达,T为一个扩频码周期。
对于m'路子载波,在卫星与接收机相对速度为v时,式(8)所对应的信号在频域的峰值应出现在处,其中,fd为基准频率f0对应的多普勒频率。因此在进行多普勒频率fd搜索时,可按照一下规则进行相干叠加:

对Zi(fd,τ')取模作为最后的检测判决量。
为进一步分析上述捕获方法的性能,将式(3)代入式(8),为简化分析,不考虑数据位跳变,忽略及α的影响,并用f代换f',可得:d,m'

式中:等号右侧第一项为纯信号项,代表导航信号,记为Sm',f',τ',第二项为交叉干扰项,记为Cm',f',τ',第三项为纯噪声项,记为n2,m'(f')。
将式(8)代入式(9)可得:
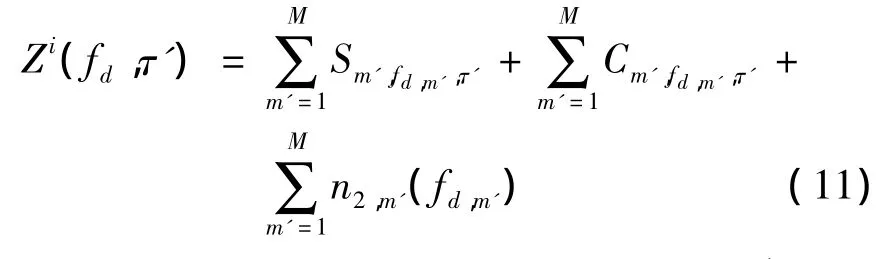
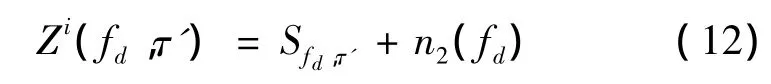
式(11)与式(12)相比,复合载波情况下,纯信号项与纯噪声项表现为多个子载波对应信号的叠加以及噪声的叠加,而单载波情况下,信号与噪声分别有单独的一个成分组成,实际上,上述不同并不改变纯信号与纯噪声之间的信噪比,当复合载波信号总功率与单载波信号功率相等时,式(11)右端第一项和第三项之间的信噪比与式(12)右端第一项与第二项之间的信噪比是相同的。
此外,式(11)相对于式(12)多出不同子载波信号之间的交叉干扰项,势必抬高基噪,进而影响总的信噪比。不同子载波信号之间的正交性(隔离性)直接反应为式(11)中交叉干扰项的大小,对交叉干扰项的控制是我们在具体设计符合载波导航信号具体参数时必须认真考虑的问题。
在第2.1节中,我们提出了两种复合载波信号的捕获框架,分别对应不同子载波采用不同扩频码和相同扩频码的两种信号设计,其中,采用不同扩频码时,捕获运算资源占用相对较大,而采用相同扩频码时,其资源占用较传统单载波BPSK导航信号没有明显增加。但从式(10)和式(11)看,不同子载波采用不同的扩频码所带来的子载波交叉干扰将明显小于采用相同扩频码时的情况,我们将在第4节中通过仿真定量分析典型情况下它们的性能。
2.3捕获性能分析
根据式(11)得到捕获检测判决量后,上述捕获方法的性能可以沿用传统信号检测与估计理论进行分析。考虑到在第3节中我们将对复合载波导航信号捕获方法的性能进行仿真分析,为了便于对仿真结果进行对比,以下简要描述信号检测性能的一些要点。
在导航信号的捕获中,为了节约计算量,通常是在码时延和多普勒频率两个维度上按照一定的间隔进行投点,由于真实的码时延或多普勒频率一般不等于投点处的值,存在偏差,进而影响检测判决量中纯信号峰值的强度。
假设在峰值附近真实码时延与投点处码时延相差ετ,由此带来的纯信号峰值的衰减量为:

式中:Tc为伪随机码码片宽度;式(13)对应的图形如图4(a)图所示。若码时延搜索步长为 τstep,最大为0.5τstep,一般取 τstep为0.5Tc,这时对应的 ητ最大为1.25 dB。
假设峰值附近真实的多普勒频率与投点处的多普勒频率εd,由此带来的纯信号峰值衰减量为[17]:

式中:Tc为伪随机码码片宽度;式(14)对应的图形如图4(b)图所示。若多普勒搜索步进为最大为0.5fstep,在FFT频域并行捕获处理中,如果不进行加密处理,对应的fstep为,这时 ε 为d,对应的η 约为3.9 dB;在FFT中进行两倍的d加密处理,对应的fstep为,这时 εd为,对应的 ηd约为0.9 dB。

图4 两大因素对相关峰值造成的衰减Fig.4 The impact of two major factors to correlation peak
对于式(11)给出的捕获检测判决量Zi,当其中存在信号时,对应的概率密度满足自由度为2的非中心 χ2分布[18]:

式中:λ对应式(11)中的第一项(纯信号项),σ2对应于第二项和第三项所代表的噪声,I0(·)为零阶修正的Bessel函数[19]。
若当前搜索的码-频槽中不存在信号,统计量满足自由度为2的中心χ2分布[20],对应概率密度函数表达式为:
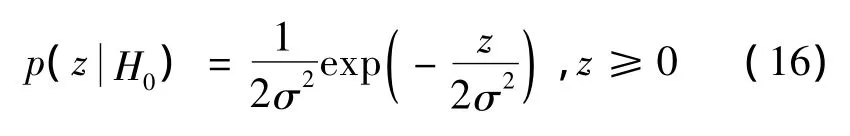
依据式(15)和式(16),在检测门限为β时,可得单次虚警概率为:
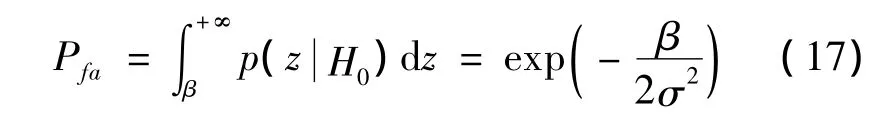
而相应的单次检测概率为:
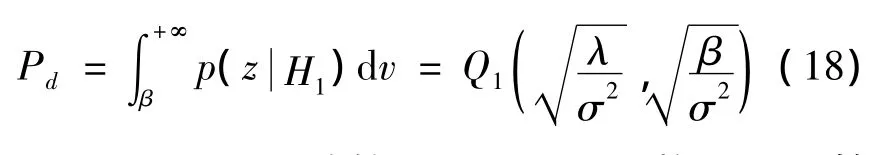
式中:Q1(a,b)是1阶的Marcum Q函数。限于篇幅,式(17)和式(18)对应的图形,我们将在第3节中结合仿真结果一并给出。
3 复合载波导航信号捕获性能仿真分析
在第2节中我们给出了捕获架构,有两种形式:通用捕获架构和简易捕获架构,其检测判决量与传统单载波信号相比增加了交叉干扰项。设定典型应用场景,通过恒虚警检测,定量评估交叉干扰项所带来影响,并与单子载波信号在检测性能方面进行对比。
实验仿真参数设定如下:各子载波功率一致;子载波扩频码采用GOLD码,码长1023chip,码速率fc=1.023 MHz;子载波间等频率间隔 Δf=2fc=2.046 MHz;子载波数M=1、2、4、6;仿真带宽30 MHz;虚警概率Pfa=10-3,蒙特卡罗仿真次数为10000。
对比复合载波导航信号各子载波信号分别采用相同伪随机扩频码和不同伪随机扩频码,即:有码隔离和无码隔离,两种情况下,分别对应采用通用捕获架构和简易捕获架构,检测性能的差异。设定复合载波导航信号子载波数目M=6,预检测积分时长为1 ms。

图5 复合载波导航信号子载波数M=6时有/无码隔离对比图Fig.5 Comparison of detection performance under the code separation or not
由图5可知,相同子载波数目情况下,对复合载波导航信号加入码隔离,采用图2所示的通用捕获架构对每一路子载波分别处理,仿真曲线与理论曲线拟合情况理想;而复合载波导航信号无码隔离,采用图3所示的简易捕获架构进行处理,仿真曲线略差于理论曲线。该仿真校验了复合载波导航信号各子载波信号采用不同伪随机码进行调制,检测性能接近理论分析;而当复合载波导航信号各子载波信号采用相同伪随机码进行调制,由于无码隔离,交叉干扰项影响凸显,导致检测性能降低。
对比分析复合载波导航信号无码隔离情况下,子载波交叉干扰项对检测性能的影响。复合载波导航信号各子载波信号采用相同的伪随机进行调制,相应的采用简易捕获架构进行处理,分析无码隔离时,子载波数目对最终检测性能的影响。其中,复合载波导航信号子载波数目M分别取2、4、6,对应检测性能如图6所示。
由图6可知,若复合载波导航信号采用相同的伪随机扩频码进行调制,随着子载波数目的增加,仿真曲线原来越偏移理论曲线。可知,子载波间互扰量随子载波数目的增加而增大,对捕获性能的影响也越来越明显。当复合载波导航信号子载波数目M=6时,子载波互扰量的影响使得检测性能与理论相比下降约0.8 dB。
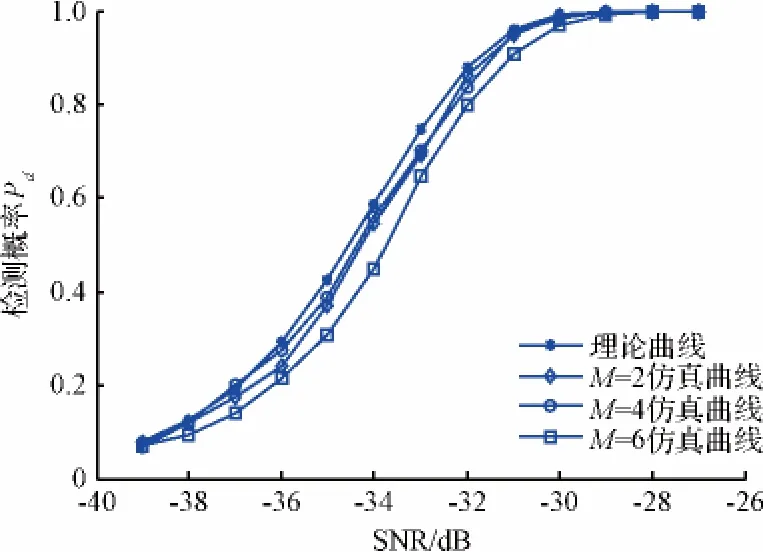
图6 复合载波导航信号简易捕获架构性能分析图Fig.6 Comparison of detection performance with different number of sub-carrier utilizing the simplify framework
对比等功率条件下,复合载波导航信号与传统单载波导航信号C/A码、P码的检测性能。复合载波导航信号各子载波调制伪码不同,相应的采用通用捕获架构进行捕获,其中,复合载波导航信号子载波数目M=5,码速率fc=2.046 MHz,信号主瓣带宽为10.23 MHz。C/A码采用4 MHz带宽进行捕获仿真,P码与复合载波导航信号采用30 MHz带宽进行捕获仿真。对应检测性能如图7所示。
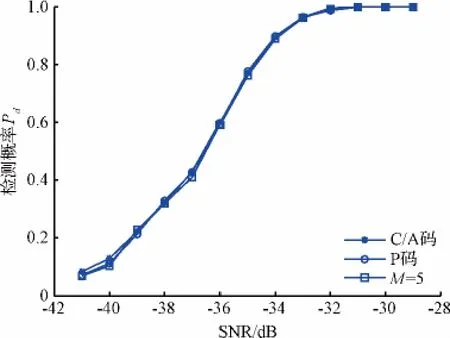
图7 复合载波导航信号与传统单载波导航信号检测性能对比图Fig.7 Comparison of detection performance of NSCCand single carriers
由图7可知,复合载波导航信号检测性能与传统单载波导航信号C/A码、P码相比,在等功率的前提下,检测性能基本相等。
4 结论
本文介绍了复合载波导航信号体制结构特点和设计思路,并针对该信号的多载波结构特征,提出了一套适用的捕获架构。该架构采用匹配滤波器配合FFT算法实现伪码快速剥离和时频域转换,并利用信号子载波频点间隔信息对信号频谱能量进行移位相干叠加实现能量积累,保证相同信噪比情况下检测性能与单载波信号相当,并且不明显增加运算量和资源占用情况。
该架构还可根据复合载波导航信号各子载波信号调制伪码的隔离度,对硬件进行精简以节约资源占用量,但也会牺牲掉部分检测性能。这为该信号体制下一步的同步算法设计工作提供了铺垫和理论支撑。
[1] 唐祖平,周鸿伟,胡修林,等.Compass导航信号性能评估研究[J].中国科学:物理学,力学,天文学,2010,40(5):592-602.[Tang Zu-ping,Zhou Hong-wei,Hu Xiu-lin,et al.Performance evaluation research of compass navigation signal[J].Science in China Series G:Physics,Mechanics and Astronomy,2010,40(5):592-602.]
[2]Pelton J N.Trends and future of satellite communications[M].New York:Springer,2013.
[3]Cui J,Shi H.Satellite communication and navigation integrated signal[J].Journal of Electrical Engineering,2013,11(8):4351-4356.
[4] 张路平,王建新,马宁.多径信道下OFDM信号和单载波信号的盲识别[J].宇航学报,2012,33(9):1289-1294.[Zhang Lu-ping,Wang Jian-xin,Ma Ning.Blind recognition of OFDM signal and single-carrier signals in multi-path channel[J].Journal of Astronautics,2012,33(9):1289-1294.]
[5]Garcia-Pena A,Julien O,Macabiau C,et al.FMT signal options and associated receiver architectures for GNSS[C].IEEE/ION Position Location and Navigation Symposium,Carolina,USA,April 24-26,2012.
[6]Emmanuele A,Luise M,Won JH,et al.Evaluation of filtered multitone(FMT)technology for future satellite navigation use[C].24th International Technical Meeting of the Satellite Division of the Institute of Navigation,Oregon,Portland,September 20-23,2011.
[7]Liu X,Liang M,Morton Y,et al.Performance evaluation of MSK and OFDM modulations for future GNSS signals[J].GPS Solutions,2014,18(2):163-175.
[8]Deng Z,Yu Y,Yuan X,et al.Situation and development tendency of indoor positioning[J].China Communications,2013,10(3):42-55.
[9]Xu Y,Yuan H.Navigation signal structure based on complex carrier modulation[J].Science in China Series G:Physics,Mechanics and Astronomy,2011,54(6):1035-1045.
[10] 佟学俭,罗涛.OFDM移动通信技术原理与应用[M].北京:人民邮电出版社,2003:66-68.
[11] 党军宏,晏坚,曹志刚.一种基于OFDM和跨层设计的星载交换方案[J].宇航学报,2009,30(3):1086-1094.[Dang Jun-hong,Yan Jian,Cao Zhi-gang.An on-board switch scheme based on OFDM and cross-layer design[J].Journal of Astronautics,2009,30(3):1086-1094.]
[12]Jovanovic V M.Analysis of strategies for serial-search spreadspectrum code acquisition-direct approach[J].Communications,IEEE Transactions on,1988,36(11):1208-1220.
[13]Spangenberg SM,Scott I,McLaughlin S,et al.An FFT-based approach for fast acquisition in spread spectrum communication systems[J].Wireless Personal Communications,2000,13(1/2):27-55.
[14]Molino A,Girau G,Nicola M,et al.Evaluation of a FFT-based acquisition in real time hardware and software GNSS receivers[C].The 10th International Symposium on Spread Spectrum Techniques and Applications,Bologna,Italy,August 25-28,2008.
[15]Borio D,O'Driscoll C,Lachapelle G.Composite GNSS Signal Acquisition over Multiple Code Periods[J].Aerospace and Electronic Systems,IEEE Transactions on,2010,46(1):193-206.
[16] 陈希,张锐,帅涛.基于FFT的GPS快速并行捕获算法[J].宇航学报,2011,32(1):162-166.[Chen Xi,Zhang Rui,Shuai Tao.A new rapid acquisition algorithm based on FFT for GPSsignals[J].Journal of Astronautics,2011,32(1):162-166.]
[17]Stirling-Gallacher R A,Hulbert A P,Povey G J R.A fast acquisition technique for a direct sequence spread spectrum signal in the presence of a large Doppler shift[C].The 4th International Symposium on Spread Spectrum Techniques and Applications,Mainz,Germany,September 22-25,1996.
[18] 夏双志,戴奉周,刘宏伟.复高斯白噪声背景下贝叶斯检测前跟踪的检测阈值设置方法[J].电子与信息学报,2013,35(3):524-531.[Xia Shuang-zhi,Dai Feng-zhou,Liu Hong-wei.A method of determining detection threshold for bayesian track-before-detection in white complex gaussian noise[J].Journal of Electronics&Information Technology,2013,35(3):524-531.]
[19] 崔嵬,朱新国,吴嗣亮.基于约束判决的二次门限检测[J].电子与信息学报,2009,31(9):2074-2078.[Cui Wei,Zhu Xin-guo,Wu Si-liang.Study on double threshold detection based on constraint judgment[J].Journal of Electronics&Information Technology,2009,31(9):2074-2078.]
[20]Srinivasan R,Rangaswamy M.Importance sampling for characterizing STAP detectors[J].Aerospace and Electronic Systems,IEEE Transactions on,2007,43(1):273-285.
