似稳条件下低频电容感应耦合探究
2015-01-24李志辉陈奋策
李志辉 , 陈奋策
(1.福建教育学院理科研修部 福建 福州 350025;2.厦门大学嘉庚学院机电工程系 福建 漳州 363105)
无极放电光源没有传统光源的电极,寿命长、节能、环保。无极放电的方式有感应放电、容性放电、微波放电和行波发电等[1]。
无极灯主要由频率发生器、功率耦合器和玻璃泡壳三部分组成,通过电磁感应方式将能量耦合到充有适量特种气体的灯泡内产生可见光。现在低频无极灯的工作频率在230 kHz左右,功率耦合器一般是采用电感耦合,还有一种最近的发明专利提出的电容耦合方式[2]。本文从电磁理论出发,以无极灯为例,阐述似稳条件下低频电容耦合的原理。
1 似稳条件的理论意义
我们知道电磁学中电路中的能量是通过电磁场来传播的[3-5],电磁能量在导体之外的空间沿着导线表面以光速传到负载,然后沿着它侧面输入,似稳电路也一样。似稳电路中与稳恒电路的相似或不相似的区别在于基尔霍夫定律成立与否,为便于腾清概念,我们把似稳电路成立的条件分为必要条件和充分条件[4]。
1.1 似稳电路成立的必要条件
似稳电路中,设电源的频率f,周期T,电路(电子仪器)的尺寸为 l,电磁波的波长为 λ,电源的圆频率(ω=2πf)较低时,似稳电路成立的必要条件
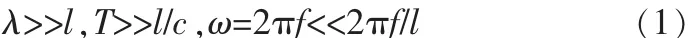
即电磁波的波长λ远大于电路的尺寸l,电磁场的变化传佈整个电路所需要的时间l/c远小于一个周期T;在l/c时间内,电流、电荷和电磁场的分布都来不及发生显著的变化;这种情况下,每一时刻电磁场的分布与同一时刻的电流、电荷的分布的关系,和稳恒电路一样,只是它们一起同步地做缓慢的变化。记电磁波通过l所需的时间t=l/c,电源的周期T=1/f大大于 t,或电源的圆频率 ω=2πf<<2πc/l。
1.2 似稳电路成立的充分条件
似稳电路成立的充分条件:交流电路中的电感和电容元件把磁场和电场集中在自己内部很小的范围内。
2 似稳电路状态与电感耦合
2.1 似稳电路状态
我们知道电路中的电磁能量是在导体之外沿着导线表面以电磁波形式光速C传到负载,似稳电路也一样。无极灯的尺寸l为几厘米到几十厘米的量级,
低频无极灯电源的频率f工作频率在230 kHz左右,f< 如图1,每个磁环上绕有N匝导线圈,磁环的磁导率为μ,单位长度有n匝导线,频率发生器(未图示)产生频率为230 kHz的正弦交变的电压(约1百伏)加到导线圈的两端,产生交流传导电流I0,满足似稳电路的必要条件[4]。假设N匝电线圈足够长,在磁环内产生的磁场的分布近似和稳恒时相似 该交变磁场又在灯泡内感应产生以为周期变化的涡旋电场,服从 图1 低频电感耦合无极灯示意图Fig.1 Low inductance coupled electrodeless lamp schematic diagram 电容功率耦合器,如图2(相当图1中包含磁环的一段)包括两电极板平行设置的电容,多个电容可以是串联或并联,缠绕在磁环2上的N匝导线圈1串联着个m(mN)电容4,即可以通过个电容提供电容耦合,又可以通过(N-m)个线圈提供电感耦合,在灯管3(只画出一段)内感应产生交变的涡旋电场,涡旋电场激发和加速管内电子,实现电磁能量耦合并导致灯管发光。 现讨论两种形式的电容:一种是叠片式(如图3),另一种为平行板式(如图4)。频率发生器(未画出)产生的频率为230 kHz的正弦交变的高电压(1百伏左右)加到导线圈的两端,产生交流传导电流I0,每个电容产生的交变的“位移电流”使电流连续。类比电感耦合情况,在交流电流变化的一个周期T内,电磁波在Δt< 图2 低频电容耦合示意图Fig.2 Schematic diagram of low frequency capacitance coupling 电磁场的理论基础是麦克斯韦方程[6], 和介质电磁性质方程构成微分形式麦克斯韦方程组,介质电磁性质最简单的关系式是 1)叠片式单个电容情况 如图3,导线圈中串接着叠片式单个电容(或薄膜电容),电路中通以交流传导电流I0,对电流产生的磁场强度H取旋度 其中 k=ω/c,推迟因子 exp(ik→·r→)在似稳条件(k=ω/c→0,t≈t′)下趋于1。式(7)化为与稳恒情况下传导电流产生的磁场强度相似的形式为: 图3 叠片式单个电容中电流分布示意图Fig.3 Schematic diagram of current distribution of laminated single capacitor 2)单个电容是平行板电容 如图4,假设平行板电容器二极板为半径为r0的圆板,在两极圆板间的边缘处取一轴对称回路L1,有 在对称近似下,可得涡旋磁场B1的计算公式为: 似稳情况下,如图 2,导线上串联着(1)和(2)形式的电容,磁环上单位长度的n圈交变传导电流,在磁导率为μ的磁环内产生的交变磁场强度与稳恒时的表达式相似 3)多个串联电容排成环状 如图5,N′个串联电容4排成环状(半径为Ra)情况,在环状电容器的外部绕有导线1的磁环2中取一轴对称回路L,在对称性近似下,可得交变涡旋磁场这里近似取磁环的半径也为R0。设单个电容板的面积为S1,N′个串联电容排成环状的电容的面积S=N′S1,磁导率为μ的半径~R0磁环内产生的交变涡旋磁场强度为: 图4 单个平板电容中电流分布示意图Fig.4 Schematic diagram of current distribution in the single plate capacitor 图5 N′个串联电容排成环状电容耦合器示意图Fig.5 N′series capacitor discharge into the annular capacitor coupler schematic diagram 以上以电磁基本理论为基础,近似计算了和推导了在似稳条件下低频电容电路产生的涡旋交变磁场和感应涡旋交变电场耦合[4]的可行性,我们在低频电容耦合的无极灯实验中也予以了证实。实验显示,电容耦合的电路呈电容性,电感耦合的电路呈电感性。 [1]陈育明,陈大华,李维德,等.LVD无极灯[M].上海:复旦大学出版社,2009. [2]陈奋策.发明专利:“一种无极灯的耦合发光方法及其结构”中国,201110156582.9[P].2011. [3]赵凯华,陈熙谋.电磁学[M].北京:人民教育出版社,1978. [4]陈奋策.似稳条件与无极灯工作原理[J].福建教育学院学报,2014(6):20-21.CHEN Fen-ce.Quasi stationary conditions and electrodeless lamp working principle[J].Journal of Fujian Institute of Education,2014(6):20-21. [5]杨通铭.稳恒及似稳电路中电磁能的传输[J].黔东南民族师范高等专科学校学报,2006,24(3):8-9.YANG Tong-ming.Tr ansmissin of electromagentic energy in stable and similar stable currents[J].Journal of Southeast Guizhou National Teachers College,2006,24(3):8-9. [6]郭硕鸿.电动力学[M].2版.北京:高等教育出版社,1997.
2.2 似稳电路下低频电感耦合

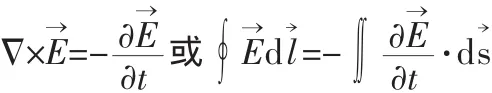
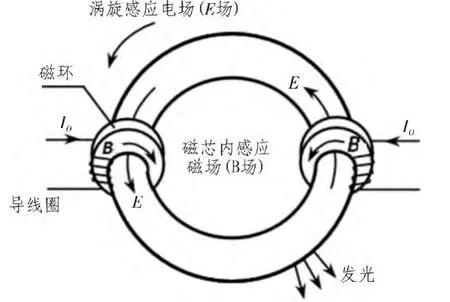
3 似稳状态下低频电容耦合的描述
3.1 似稳电路下低频电容耦合器的物理图像
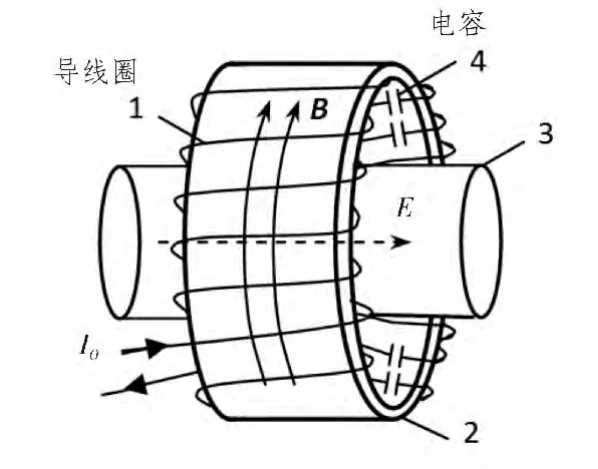
3.2 似稳状态下电容耦合的电磁场理论分析
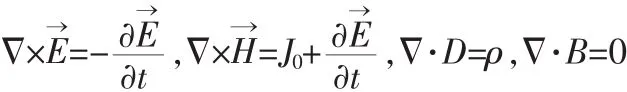




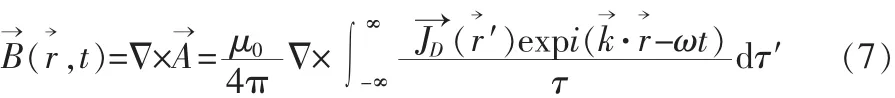


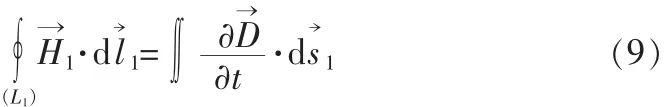






4 结 论
