基于Matlab的数字音符实时显示研究

郭之亨，周 华，李良荣

（1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；2.贵州电子信息职业技术学院 通信工程系，贵州 凯里 556000）

随着我国经济的持续快速发展，百姓的生活水平不断提高，人们已不仅满足于物质生活方面的需求，而是更多的转向精神文化生活层面。作为精神生活重要组成部分的，各种形式的音乐在民众中扮演着越来越重要的角色。

随着计算机技术的发展，很多音乐的处理是通过计算机完成的[1]，之前已有大量的文章是运用Matlab来研究音乐的，但都不是研究音符实时显示的。本文借助Matlab软件，通过简易谐波峰值法算法[2]及时将乐器发出的乐音转变为简谱音符并实时显示出来，这将有助于人们进一步了解和学习音乐，降低音乐学习门槛，有很强的现实意义。

1 简谱的主要构成

简谱分字母简谱和数字简谱[3]，本文所说的简谱皆指数字简谱，而本文中提到的各频率对应的音符皆为C调下的音符。

一般来说，构成简谱的基本要素中最重要的是“音的高低”和“音的长短”。表示音的高低的基本符号，用7个阿拉拍数字标记。它们的写法和读法如表1所示[4]。音的长短是在基本音符的基础上加短横线、延音线等符号来表示的。

表1 简谱音符及读音

2 基于Matlab音符的实时显示

2.1 显示原理

每个不同的音调对应着不同的音符。而音调由基音频率决定[5]，比如音符“3”对应 659 Hz，音符“4”对应 698 Hz，所以音符的显示，首先是要准确提取出每个乐音的基波频率[6]，进而通过一定的数学关系转化成数字音符表示。本设计采取谐波峰值法提取基波频率，该算法依据的原理是每个乐音经傅里叶变换后其基波频率对应的幅值最大[7]。给数字音符添上相应短横线，附点等就可完成音长短的表示。表2所示给出C调各音符对应频率值[8]。

2.2 实验方法

音调显示：本次实验，首先将待处理的音乐片段录入到电脑里，实验过程中采样频率为16 000 Hz，采样时间为8 s。将存入电脑的音频输入Matlab软件中，对其分段（每段时长125 ms）进行快速傅里叶变换，从频谱中找到幅度最大的谱线，对应频点与频率分辨率乘积即为所求基波频率。一个时长 （125 ms）的音频经快速傅里叶变换之后的频谱图如图1所示。

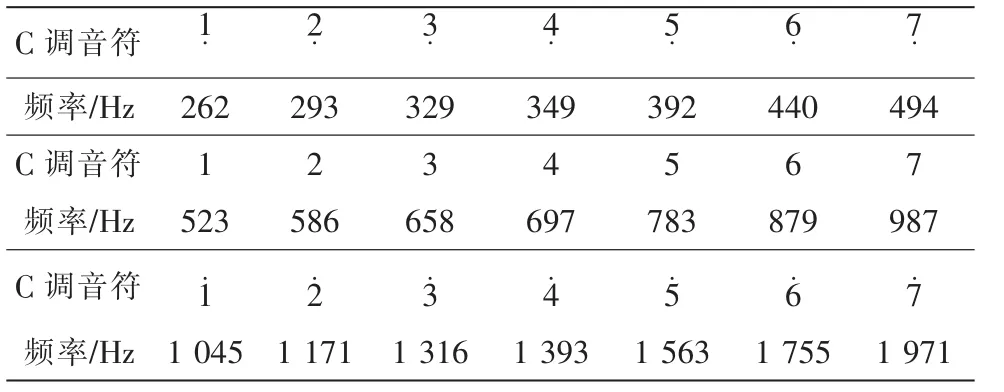
表2 C调各音符频率值对照表Tab.2 The frequency of each C tone note comparison table

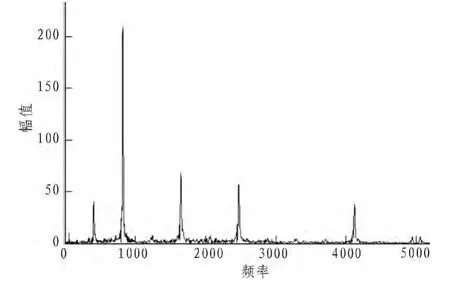
图1时长125 ms的音频快速傅里叶变换频谱图Fig.1 The frequency spectrogram of 125 ms audio FFT

对应Matlab程序如下：

fs=16000； %取样频率16 000 Hz

duration=8； %录音时间8 s

pause；

x=wavrecord（duration*fs，fs）； %进行录音，x 为音频信号

y=[]； %建立一个名为y的空数组，用于存放基波频率值

for i=1:2000:（length（x）-1999） %对信号进行分段

y=[y，2*min（find（abs（fft（x（i:i+1999，:）））==max（abs（fft（x（i:i+1999，:））））））]；

end %使用 abs（fft（））对信号分段进行 fft变换并取幅值，用max（）和find（）函数找出每段最大谱线及其对应的频点，对应频点乘以2即为每段基波频率，将结果存于y中

取两个相邻音符频率的平均值为分界，若频率低于平均值则显示为相邻两个音符中，音调较低的音符，反之则显示为二者中较高的音符。如音符“3”、“4”对应频率分别为329 Hz和349 Hz，平均值为339 Hz，则频率在329~339 Hz之间的皆显示为“3”，在339~349Hz之间的皆显示为“4”。本次实验研究的频率段为250~1990 Hz，超出该频段对应的音符皆为休止符“0”。

音的长短显示：待处理音频，每125 ms进行一次快速傅里叶变换。一般四分音符持续时间为400~500 ms，这里设定为500 ms[5]。八分音符持续时间为四分音符的一半，而十六分音符持续时间又为八分音符的一半。所以每次快速傅里叶变换之后提取的音符应为十六分音符。本次设计以四分音符为一拍，每小节四拍，每小节之间用小节线“|”隔开。若两相邻音符相同，则合并为一个持续时间是其二倍的上一节音符。如“11”合并为“1”。如表3所示为音符“1”的各时长：

表3 音符“1”的各时长表示形式Tab.3 Each length of time displaying of note “1”

由于Matlab命令窗口中无法显示某些音符格式，对此本次设计做了一些调整，以音符“1”为例，如表4所示。

表4 格式对照表Tab.4 Format table

图2和图3所示为对一段8 s音频检测之后所得到的各分段基音频率及最终的音符显示。

图2一段8 s音频经Matlab处理之后所得各分段基因频率（截图）Fig.2 The fundamental frequency of each segment after a 8 s audio processed by the Matlab （screenshot）

上述结果很好地区分显示了各音符的音调高低和时长，按每四拍一个小节准确划分成4个小节，取得了预期效果。

我们正在研究翻译工具，将图3所示数据翻译成图4所示的音乐简谱：

图4 Matlab数据翻译的音乐简谱Fig.4 Numbered musical notation translated by the Matlab

3 结束语

本次设计比较准确的提取出了被测音频的基音频率，并将其转化为对应音符显示，其重点在于基音频率的提取。本次设计只能提取单独一种乐器发音时的基波频率，对多种乐器同时发出的混合音则失效，这是将来努力研究、改进的方向。本次设计在一些地方进行了简化处理，比如规定采样时间为一固定时间，文中音符全为C调下的音符，每四拍为一小节。这样做使得程序更加简洁，软件运行起来也更加流畅。Matlab中显示的数据只有专业人事可以阅读，对于音乐爱好者有难度，还需要研制一个简谱翻译工具，这是我们下一步的又一个研究目标。

[1]杨行峻，迟惠生.语音信号数字处理[M].北京：电子工业出版社，1995.

[2]张红，宋俊寿，黄泰翼.一种新的峰值提取方法及其在语音基频提取中的应用[J].铁道学报，1998（6）:68-73.ZHANG Hong，SONG Jun-shou，HUANG Tai-yi.A novel peak picking algorithm and its application in extraction of fundamental frequency of speech signal[J].Journal of the China Railway Society，1998（6）:68-73.

[3]白云.首调唱名法与简谱的传入及其在我国视唱练耳学科发展中的意义[J].黄河之声，2010（21）:74-75.BAI Yun.The introduction of tonic sol fa and numbered musical notation and its significance in the development of the solfeggio subject in China[J].Yellow River of the Song，2010（21）:74-75.

[4]李重光.基本乐理通用教材[M].高等教育出版社，2004.

[5]张盼盼.Matlab的音乐合成器应用[J].企业导报，2011（11）:297-298.ZHANG Pan-pan.Application of matlab music synthesizer[J].Cuide to Business，2011（11）:297-298.

[6]刘丹，朱汉城.音乐特征识别的研究综述[J].计算机工程与应用，2002（24）:74-77.LIU Dan，ZHU Han-cheng.A review on the research of music features recognition[J].Computer Engineering and Applications，2002（24）:74-77.

[7]于拾全，景新幸，刘志国.乐器音高检测方法的比较和精度分析[J].电声技术，2006（7）:4-7.YU Shi-quan，JING Xin-xing，LIU Zhi-guo.The study and realization of electronic tuning device[J].Audio Engineering，2006（7）:4-7.

[8]许锦生.电子乐谱的设计与若干关键技术的实现[D].长沙：国防科技大学，2012.

[9]叶霖，李雄飞，刘丽娟，等.一种有效识别 MIDI文件中主旋律音轨的方法[J].计算机应用与软件，2010（1）:48-50.YE YE Lin，LI Xiong-fei，LIU Li-juan，et al.An effective method for identifying the mesound track in midifiles[J].Computer Applications and Software，2010（1）:48-50.