一种改进的相位噪声抑制方法
2015-01-24王赓浡战勇杰陈茹梅
王赓浡,战勇杰,陈 昕,陈茹梅
(航天恒星科技有限公司 北京 100161)
随着卫星数传技术的不断发展,卫星需要同时传输的数据量级在不断地提高,已经由Mbps级向Gbps级发展,与此同时,采用的调制解调方式也从BPSK、QPSK升级为8PSK,中继卫星可能会发展16QAM甚至更高阶数的32QAM。相比低阶调制解调方式,影响高阶解调性能的因素增多,其中,相位噪声是影响高阶解调性能的主要因素之一。相位噪声通常存在于接收机的本振源和其他频率合成设备之中,在高阶解调中相位噪声的影响表现尤为明显。针对相噪的影响,研究者做了很多研究,文献[1-2]提出了基于自适应算法的FIRALE算法对相位噪声的影响进行抑制。基本算法能够对相位噪声进行抑制和补偿,但补偿效果有限,在噪声出现较大波动时补偿能力会下降[3]。
本文给出一种改进的相位抖动补偿方法,与之前的相位噪声抑制的算法相比,主要的改进在于引入相位噪声的方差统计和预测部分信息来提升对相位噪声的抑制能力。并通过matlab仿真证明了改进算法的优越性。最后总结本文结论。
1 基本抑制算法
受相位噪声干扰后,经过解调的基带信号s(t)的表达式如式(1):

式中φ(t)为相位噪声造成的信号相位抖动的角度,A为信号幅度,n(t)为白噪声。基本算法和本文的算法主要都是针对于 φ(t)的抑制和补偿。
文献[1-2]中提出了一种基于LMS算法的噪声影响抑制算法,LMS算法的基本原理:
LMS输出信号:

LMS误差信号:

LMS权重迭代:

其中 w(k)=[w0(k),w1(k),…wL-1(k),],φ(k)=[φ0(k),φ1(k),…φL-1(k),]分别是相应权重系数和相位噪声的 L 行的列向量。在以上3个式子当中:φ(k)为自适应滤波的输入信号;θ(k)为自适应滤波的输出信号,e(k)为误差值,wi(k)为权重系数,L为自适应滤波器的阶数,μ为收敛步长。步长是表示迭代快慢的物理量,在不同幅度的相位抖动下,同一个步长μ补偿效果是不同的。上文所述的基本算法结构如图1所示。

图1 基本算法结构图Fig.1 Structure of basic algorithm
如图1所示,基本补偿算法的运算过程为:接收信号经过硬判决得到信号,实际相位与判决后相位之差设为φ(k),k)为 LMS 算法的输入信号,输入信号 φ(k)与系数 w(k)相乘得处理后的输出信号 θ(k),然后计算得误差信号 e(k),根据经验确定补偿的步长μ,根据MMSE准则计算出相应的更新系数W(k+1),然后对下一个噪声信号进行补偿。在整个算法处理过程之中,系数更新过程是作为算法处理的核心步骤:W(k+1)=W(k)+2μ*e(k)*φ(k)。 根据以上公式算法更新系数值W(k+1),获得相应的相位抖动补偿值,不同的步长值补偿值也不同。
相位噪声是瞬时变化的噪声,其中一部分相位噪声是稳态随时间变化的,另一部分是在通信过程中瞬时变化的,基本的算法在相位噪声瞬时变化剧烈的时候,并不能很好的补偿由相位噪声造成的干扰,会造成算法性能的下降。进一步噪声变化剧烈的情况下还会造成算法收敛失败,误差系数e(k)不能收敛在一定的范围内时,甚至会造成经算法补偿后的信号出现较大的偏差[4]。
2 改进算法
针对在相位噪声的瞬时变化剧烈时,基本算法的性能出现下降的现象[5-6],本文给出了一种改进的相位噪声算法,改进算法能够在变化程度不同的相位噪声中保持较好的性能。改进后算法的结构图如图2所示。
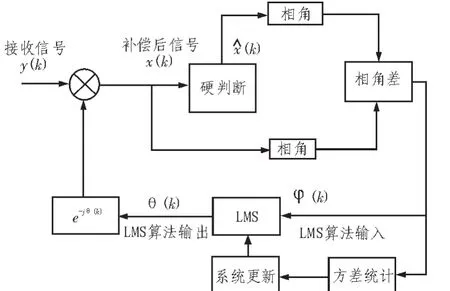
图2 改进算法结构图Fig.2 Structure of improved algorithm
根据图2改进算法的主要工作流程分为3步,首先对相位噪声进行定长度的提取;然后通过内插算法预测出相应的相位噪声数据,计算相应的相位噪声方差,根据相应的数据方差确定相应的LMS算法步进值;最后得到的相位噪声数据经过算法的延迟、收敛、补偿的相应步骤,进行相位噪声的补偿,输出补偿后的数据。改进算法的工作原理如下:
基本的LMS算法中的权重系数更新的公式(5):

在公式中主要的参数为步长μ,步长μ是表示迭代快慢的物理量,步长μ越小,算法收敛时间越长,算法精度越低,但算法应对变化剧烈的相位噪声时稳定。步长μ越大,算法收敛时间越短,算法精度越高,但在相位噪声变化剧烈的情况下算法性能下降,并且算法易收敛失败[7]。本次设计的改进算法在对相位噪声数据进行预测和统计之后,处理噪声数据获得相应的噪声方差,并以方差为参数改变步长μ的大小,适应变化程度不同的相位噪声。
利用维纳-何普方程对相位噪声进行预测,系统中接收到的信号可以简化成如公式(6):

公式中 rk为接收到的信号,pk为接收的数据信号,ejφ为相位噪声造成的相位抖动,qk为加性白噪声。本次设计利用接收数据pk前的L位数据来内插出预测的相位噪声数据,假设 xk=ejφ+qk/pk,相应的接收到前 L位的相位噪声数据如式(7):

根据得到的相位噪声的数据,由维纳-何普方程计算和预测相应的相位噪声数据,维纳-何普方程如式(8):

其中Wk为滤波器系数,Xk为相应的相位噪声检测数据。Wk滤波器系数根据式(9)计算:

其中R为前L位相位噪声信号的观测的相位噪声数据Xk的自相关矩阵,R可以根据接收的数据帧头信号的噪声观测数据计算,可以通过预先测量和熟练数据来预置。p为噪声的观测数据和噪声的旋转数据的和互相关向量。互相关向量p可以通过预先训练设置,也可以根据实际信号测量获得。
本次设计根据不同的方差值设定阈值,即根据相位噪声的方差值设定不同的步进值μ。本次设计中采用的两种不同的步进值μ(0.1和0.5)。当相位噪声的方差值在大于0.02的区间时,采用较小的步进值μ(μ=0.1)使算法收敛,当相位噪声的方差值在0到0.02之间时采用较大的步进值μ提高算法性能,使通信系统获得较高的解调性能和较低的误码率。
3 仿真验证
仿真系统采用AWGN信道模型,相位噪声模型采用经验谱噪声模型产生相位噪声[8]。采用16QAM调制解调方式。根据上文所述,加入的相位噪声方差为0.002到0.05随机变化,模拟相位噪声数据出现剧烈变化的情况[9-10]。图3的星座图依次为加噪声后、基本算法处理后结果、本文算法处理后结果。在变化的相位噪声的影响下,基本算法对于噪声有补偿效果,可以使星座点收敛。本文设计的算法对于噪声的补偿效果更好,对于星座点的收敛效果更好。
从误码率曲线对比两种算法对于相位噪声的性能,在变化的相位噪声下,基本的算法处理后和改进后的算法处理后的误码率对比如图4所示。

图3 对比星座图Fig.3 Contrast constellation
从图4可以看出改进算法的补偿效果更好,在10-4的误码率情况下,相比基本算法信噪比性能提高了1.8 dB左右。能够更好的对相位噪声带来的干扰进行抑制和补偿。
综上所述,从基本算法的补偿性能和改进算法的补偿性能对比可以得出在相位噪声变化剧烈,基本算法的补偿效果不是很好,而相应的改进算法补偿效果相比基本算法有很大改进,星座图收敛效果更好,且在10-4的情况下,信噪比性能提升1.8 dB。
4 结 论

图4 改进算法的误码率曲线Fig.4 Ber performance of 16QAMbetween basic algorithm and improved algorithm
文中提出的改进算法主要是针对相位噪声剧烈变化,基本算法性能出现下降的情况提出的。改进算法对相位噪声进行预测与估计,计算估计的相应的相位噪声的方差,并针对不同的方差值选择不同的步进权值μ进行噪声消除。通过星座图,误码率曲线对比证明了改进算法能够更好地适应实际应用情况,即无论在相位噪声剧烈变化的情况下,还是在相位噪声平稳变化的情况下,均能达到较好的算法补偿效果。
[1]陈赟,曾晓洋,陈琛,等.一种低复杂度的消除相位噪声的方法[J].中国图像图形学报,2009,14(10):2114-2115.CHEN Bin,ZENG Xiao-yang,CHEN Chen,et al.A lowcomplexity phase noise cancellation scheme for OFDMsystem[J].Journal of Image and Graphics,2009,14(10):2114-2115.
[2]Sugar G L,Tretter S A.Convergence properties of optimal adaptive carrier phase jitter predictors for sinusoidal jitter[J].IEEE Trans on Communications,1995,43(1):225-228.
[3]Fan Hu,Lidong Zhu.Performance analysis of MPSK demodulation with different phase noise spectral shape[C]//International Conference on Communications,Circuits and Systems,2009:77-80.
[4]张贤达.非平稳信号分析与处理[M].北京:国防工业出版社,2001.
[5]张安莉,陈丹.一种变步长的适应滤波算法在信号消噪中的应用[J].西安工业大学学报,2010,30(1):71-74.ZHANG An-li,CHEN Dan.A variable step-size adaptive filter used in noise reduction[J].Journal of Xi’an Technological University,2010,30(1):71-74.
[6]曹斌芳,何怡刚,李建奇.3种改进型LMS算法在噪声抵消中的仿真比较[J].电声技术,2007,31(9):66-69.CAO Bin-fang,HE Yi-gang,LI Jian-qi.Simulating comparison of modified LMSalgorithmsin noise cancellation application[J].Audio Engineering,2007,31(9):66-69.
[7]HWANG JK,LIYP.Variable step-size LMSalgorithm with a gradient-based weighted average[J].Signal Processing Letters,IEEE,2009,16(12):1043-1046.
[8]Wu J.APSK Optimization in the presence of phase noise[C]//Image and signal Processing,2009:1-5.
[9]Simon V,Senst A,Speth M,et al.Phase.Noise Estimation via Adapted Interpolation[J].IEEE GLOBECOM,2001,6(2):3297-3301.
[10]Suyama S,Onodera J,Suzuki H,et al.Decision-directed phase noise compensation for millimeter-wave single carrier systems with iterative frequency domain equalization [J].International J.Micro and Wireless Tech,2010,2(3-4):399-408.
