物理教学中突出过程、感悟方法例谈

朱亚

物理教学的根本目的就是全面提高学生素质，而学生素质的提高应该落实在物理教学过程的方方面面、点点滴滴之中.追寻科学细致的教学过程，防止重结论轻过程的不良倾向，铺就了物理教学的成功之路.

一、突出实验探究过程

实验是物理学建立与发展的基石，是学生建构物理知识、提高科学素养的重要途径.实验设计的目的与原理，实验器材的选择与组合，实验步骤的制定与实施，实验数据的测量与处理，实验现象的观察与描述，实验结果的分析与评价，构成了实验教学的完整过程和全部内容.当下，实验教学没有得到应有的重视，只在黑板上讲实验，只用多媒体模拟实验，不让学生亲自动手实验的教学现象严重存在.

（一）经历实验过程，感悟实验方法技巧，树立严谨的科学作风

学生只有亲历实验过程，才会深切感悟其中的一些思想方法，学会一些操作技巧，形成一定的实验操作技能，才会真正体会“细节决定成败”的含义.

在用油膜法估测分子大小的实验中，油酸酒精溶液如何配制呢？实验中，由于使用的盛水盘不可能很大，盘中水的表面积约为0.1m2.如果用滴管（或注射器）将一滴纯油酸滴入水中，理论上可以估算出形成的单分子油膜的面积将远大于盛水盘中水的面积.因此，必须先将油酸进行稀释，制成油酸酒精溶液，再滴一滴该溶液于盛水盘中进行实验.实验表明，油酸与油酸酒精溶液的体积比在1∶400左右比较恰当.那么，如何配制该溶液呢？如果向1mL油酸中加入酒精，均匀混合后直到总量达到400mL，即可制成1∶400的油酸酒精溶液.但这样做却存在着两个问题，第一是取的油酸体积较小，测量的相对误差较大;第二是一个班级（甚至一个年级）一次实验用去的油酸酒精溶液量太小，而配制的溶液较多，大部分浪费了.为了克服上述不足，可以采用二次配制法：第一次向5mL油酸中加入酒精，均匀混合后直到总量达到100mL，制成1∶20的油酸酒精溶液，再取该溶液5mL并向其中加入酒精，均匀混合后直到总量达到100mL，即可制成体积比为1∶400的油酸酒精溶液.

再如撒痱子粉的方法.实验中，为了便于看清单分子油膜的边缘，先要在水面上均匀地撒一层薄薄的痱子粉，所撒痱子粉是否符合要求将直接关系到实验的成败.那么，如何才能便于控制地、随心所欲地在水面上撒上符合要求的痱子粉呢？将痱子粉放入广口瓶中，用3层纱布包裹瓶口，将瓶口向下对着水面，拍打瓶底即可（要根据实际情况，调整拍打瓶子的力度）.

（二）经历实验过程，唤醒理性探究欲望，养成学以致用的好习惯

在实验中，学生会观察到一些新奇的现象，教师要因势利导，让学生产生强烈的从理论上解释现象成因的迫切需求，巩固所学物理知识，提高应用能力，逐步树立理论指导实践、实践检验理论的辩证思想.

如图1所示，在描绘小灯泡伏安特性的实验中，供选择的滑动变阻器R有两个，全阻值分别是R1=10Ω，R2=200Ω.学生通过实验比较发现，用R2时小灯泡上电压电流调节很不方便，引发了从理论上探讨实验现象产生原因的兴趣.经过研究，有的学生推导出小灯泡分得电压U随滑动变阻器触头从左端向右滑过的阻值Rx的表达式，有的学生手工绘制了U—Rx图象，有的学生还用软件绘制了U—Rx随R变化的动态图象.

（三）经历实验过程，发挥创造潜能，享受成功乐趣

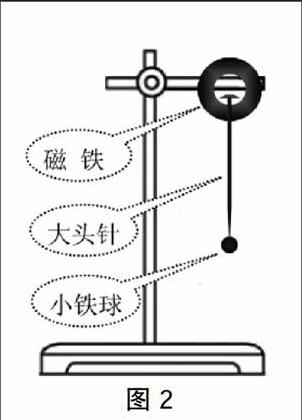
观察泊松亮斑，要求学生自行选择器材，安装装置，进行实验.学生经过深入思考、相互讨论和反复实验比较，不断优化实验设计，创造性地提出了自己的实验方案.方案一：如图2所示，在铁架台上吸一块小磁铁，小磁铁上吸一枚大头针，让大头针处在竖直方向上，且有一部分在磁铁下方，大头针被磁化后能将小铁珠吸在下端，小铁珠象被悬挂在空中一样，让激光射到不透光的小铁珠上，在屏上可以清晰地观察到泊松亮斑.方案二：在透明的胶片上，用笔描绘半径不同的一组圆形小黑点，也可以用打印机在胶片上打上小黑点（这样形成的小黑点比较规则美观），将胶片夹在铁架台上，让激光射到小黑点上，在后面的屏上可以清楚地观察到泊松亮斑.

在这样的实验设计过程中，学生会遇到较多的疑难和困惑，需要用智慧和创造来应对.每当他们最终完成实验获得成功时，内心喜悦激动之情常溢于言表.这样的实验，不仅能激发学生学习的潜能，还能增强他们学习的兴趣和走向成功的信心.

（四）经历实验过程，增强问题意识，提高解决问题能力

在探究弹簧弹力与弹簧伸长量关系时，学生必然要面对并思考下列问题：①弹簧的形变量如何测量？②如何测量弹簧产生的弹力大小？③设计怎样的表格来记录数据？④实验数据如何处理？经过分析讨论，用如图3所示的实验装置.合理的表格设计如表1.运用图象法处理实验数据，能直观地反映出弹簧弹力与弹簧伸长量成正比的关系.

表1

从问题的提出到最终解决，学生要经历一系列的研究过程，有分析综合，有假设推理，有反思调节，有优化筛选，等等.学生的知识在实验中得到巩固，学生的能力在实验过程中得到提高，学生的情感、态度与价值观在实验中得到发展.

二、突出概念和规律的理性建立过程

物理学是一门带有方法论性质的学科，理解概念、掌握规律是物理学习的重要内容.在物理概念和规律的建立过程中潜藏着丰富的思想方法，蕴含着重要的科学方法教育价值.下面通过两个具体例子，仅就渗透的方法教育和能力培养方面进行分析说明，其实这两方面是融为一体的.

（一）在概念和规律的建立过程中渗透科学方法教育

以“电容器电容”教学为例.为了使学生清晰地建构电容的概念，理解电容的物理意义——反映电容器自身特性而与其是否带电、带电多少无关.在用■定义电容前，需要得出电容器两板间电压U与其带电量Q成正比的结论.这用实验的方法很难做到，可以引导学生用微元法进行理论分析.将电容器两极板上的电荷分割为若干小部分，以至在计算每小部分在电容器两板间某点P产生的电场强度时都可以看成点电荷，设各部分电荷在P点产生的合场强为E=k■，两板间电压U=Ed.现让电容器带电量变为原来的n倍，极板上分割的部分不变，则每一部分带电量均为原来的n倍，根据点电荷电场强度的计算公式可知，每一部分在P点产生的场强都为原来的n倍，合成后P点合场强必为原来的n倍，由U=Ed可知，两板间电压必为原来的n倍，因此电容器两板间电压U与其带电量Q成正比.所以■与电容器带电多少无关，对不同电容器■又会不同，因此■一定是描述电容器自身特性的物理量，将它定义为电容器的电容C=■.从方法上看采用的是比值定义法，经过定义前的详细分析过程，能让学生比较深刻地感受比值法定义物理量的特点及其科学性.endprint

为了让学生进一步理解电容是反映电容器容纳电荷本领的物理量，可从以下两个方面着手分析.第一，从电容的数值意义上分析，由定义式C=■得，电容在数值上等于两板间电压为1V时电容器需要带的电荷量，比较不同的电容器，在两板间电压均为1V这个同等条件下，电容器所带的电荷量越多，其电容就越大，可见，电容是反映电容器容纳电荷本领的物理量.由电容器的定义式进行简单的数学变换易得C=■，因此电容在数值上又等于两板间电压增加1V时电容器增加的电荷量，可见，电容是反映电容器容纳电荷本领的物理量.第二，用类比法帮助理解.将电容器和水容器进行类比，电容器带的电荷量—水容器装的水量（水的体积），电容器两板间的电势差—水容器上下两个液面的高度差（即水深度），电容器的电容—水容器的横截面积，要使水容器中水深相同，横截面积大的水容器装的水多，同理，在电势差相同时，电容大的电容器带的电量就多，可见，电容是反映电容器容纳电荷本领的物理量.

研究影响平行板电容器电容的因素时，首先依据C=■，保持Q不变，改变两板间距离d等相关因素，通过U的变化情况，建立C与d等相关因素的关系，这里用了转换思想方法.其次，用如图4所示的实验研究过程，定性分析平行板电容器电容的决定因素时，运用了控制变量法.还可以运用控制变量法，结合静电场知识，借助电场线，直观形象地进行推理分析，定量得出C∝■规律.

（二）在概念和规律的建立过程中贯穿思维能力培养

以理想变压器电压变比公式建立■=■为例.该公式通常是在实验测量的基础上，通过分析实验数据总结出来的.教学中再给出如下推导，让学生进行是非分析和价值评价.如图5所示，理想变压器的原、副线圈匝数分别为n1、n2，原线圈加交流电压U1，副线圈产生电压为U2，则根据法拉第电磁感应定律得

E1=n1■，       E2=n2■.

对理想变压器，有U1=E1，U2=E2，

所以■=■=■.

上面的推导似乎很有道理，无懈可击.其实隐藏着问题，因为根据法拉第电磁感应定律得到的E1、E2是感应电动势的平均值，而U1、 U2指的是原、副线圈两端电压的有效值，所以上面的推导有问题;但如果令Δt→0可得瞬时值之比，对于正弦交流电，仅从数值上而不是意义上分析，有效值一定会等于某一时刻的瞬时值，因此附加这样的分析说明后，上面的推导又是正确的.教学中，组织引导学生对规律形成中似是而非的有关问题进行讨论，有利于提高学生思维的深刻性、批判性等思维品质.

三、突出问题分析解决过程

学贵在思，思源于疑，有疑问才有认知需求，才能产生积极思维，这表明提出问题十分重要.其实，分析解决问题同样重要，在问题的分析解决过程中，突出分析方法，对培养学生思维的逻辑性、科学性，提高学生的思维能力意义重大.下面举两个例子说明.

（一）经历典型问题分析解决过程，学习分析方法

如图6所示，电场线是曲线，在电场线上某点由静止释放一个带正电的点电荷，设电荷只受电场力的作用，试证明电荷运动轨迹与电场线不重合.

这是学习“静电场”时极其常见的问题，几乎每本高中物理资料讲到“静电场”一章时都会涉及该问题，又是师生讨论时不易透彻地把道理说清楚的问题，究其原因，主要是分析方法不恰当，若从正向推理论证，就是说不清楚.引导学生用反证法：如图6所示，假设电荷沿电场线做曲线运动，在运动中的任一状态，受力的方向与电场强度方向相同，沿电场线在该点的切线方向，又因为速度方向沿轨迹在该点的切线方向，所以受力方向与速度方向就沿同一方向，根据力和运动的关系可知，物体将做直线运动，这个结论与假设的电荷沿电场线做曲线运动矛盾，因此假设不正确，所以电荷一定不沿电场线运动.以上分析推理严密，论证有力，彰显了反证法强大的逻辑力量，突出了方法举足轻重的作用.

（二）经历典型问题分析解决过程，提升思维品质

如图7所示的电路中，有一个理想变压器，原线圈匝数为n1，串联一只小灯泡A，再并联一只电压表V1后接在稳定的交流电源上;副线圈匝数为n2，串联灯泡B和滑动变阻器R，B灯上并联电压表V2.现在向下移动滑动变阻器R的滑动触头P，下列判断正确的是

A.V1读数将变大，V2读数将变小

B.V1读数将变小，V2读数将变大

C.灯泡A和B上消耗的功率都变小

D.灯泡A及B上消耗的功率都变大

分析：设电源电压为U，原、副线圈两端电压分别为U1、U2，电流分别为I1、I2，灯两端电压分别为UA、UB，推理解答的流程图如下：

由于I1、I2都减小，所以灯泡A和B上消耗的功率都变小，选项AC正确.

质疑：上式推理过程中，标注①处是将U2当作不变处理的.而循此推下去到标注②处又推得U2增大.如果U2增大，则由R增大在标注①处将推不出I2减小.因此上述推理过程有问题，所得结论值得怀疑，怎么办？

释疑：在向下移动滑动变阻器R的滑动触头P使R增大时，引起I2的变化情况无非有三种，即增大、不变和减小.假设I2增大，则有如下推理，会得出矛盾结果：

因此，I2不可能增大，同理可以证明I2不可能不变.排除掉I2增大、不变两种情况，I2就只能减小.可见，要逻辑严谨地解决本题，必须采用排除法和假设推理法.在问题分析解决过程中，有意识地将学生引进一时难以自拔的疑问中，让其孜孜以求、“苦苦挣扎”，对培养其逻辑思辨性，提高思维能力有很大价值.endprint