蒸汽发生器传热管流致振动线性分析程序的研发
2015-01-23王德元何世贤
□吕 红 王德元 何世贤 蒋 娜
一、引言
蒸汽发生器传热管的完整性对于蒸汽发生器乃至整个核电站的安全运行至关重要。二次侧流体的横向冲刷引起的传热管振动是导致管壁磨损、破裂、疲劳失效的主要原因之一。横向流作用下流体诱发振动的机理主要有:流弹不稳定性、湍流激振和旋涡脱落等。国外各大核电公司都有自己专用的蒸汽发生器传热管流致振动分析程序,如美国西屋公司的“FLOVIB”、加拿大巴威公司的“LINFIV”及法国阿海珐公司的“GERBOISE”等。近年来,国内也有相关研究者采用商业软件针对核电站蒸汽发生器传热管流致振动进行了线性分析计算,然而,国内依然尚无专用的分析程序。因此,我国大部分蒸汽发生器设计和性能分析都采用国外专用软件进行传热管流致振动分析计算。国外专用软件价格昂贵,有些软件无法获得程序的源代码,且适用范围不广泛,从而在较大程度上限制了应用范围。
本文根据ASME 规范,基于流弹不稳定性和湍流激振的成熟理论和经验关系式,采用面向对象思想,自主开发蒸汽发生器传热管流致振动的线性分析程序。假设传热管与支撑板以及传热管与防振条之间不存在间隙,即所有支撑均为有效支撑,计算某型号蒸汽发生器传热管的流弹不稳定率和湍流响应值,并与国外专用软件的分析结果进行了对比。
二、数学模型
(一)传热管模态分析。传热管模态分析时,管内一次侧流体和管外二次测流体对管子的影响作为附加质量考虑,传热管的等效质量为:

其中,ρt是传热管密度;ρp是一次侧流体密度;ρs是二次侧流体密度;C 是流固耦合系数;Do和Di分别是传热管的外径和内径。
(二)流弹不稳定性。根据ASME 规范,当有效激励速度与临界速度之比小于1 时不会出现传热管流弹失稳现象。核工业中为保守起见,一般把比值0.75 作为判断传热管是否发生流弹失稳的标准。本文采用Connors 模型计算流弹不稳定性临界速度:

其中,β 是Connors系数;fn是固有频率;ζn是阻尼比;m0是传热管单位长度的平均总质量;ρ0是二次侧流体的平均密度。UEn是第n 阶模态的有效激励速度,当横向流的速度和密度不是常数时,其计算关系式如下:
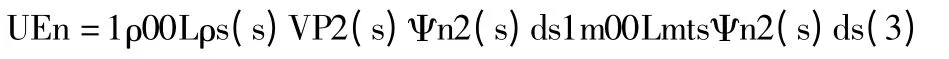
其中,ρs(s)是二次侧流体密度,L 是传热管长度,s 是传热管的曲线横坐标;Ψ 是模态振型,由模态分析得到:Vp是管间横向速度。
(三)湍流激振。对于蒸汽发生器传热管而言,轴向流引起的湍流激励和横向流相比可以忽略不计,故本文只考虑横向流引起的湍流激励。湍流激励响应的半经验计算关系式为:

其中,σn(s)是第n 阶模态的均方根位移;¯v 是二次侧平均管间速度;k 是自由度;L0和D0是传热管参考长度和参考外径;αn是模态相关因子。
沿着管子总的均方根位移通过模态叠加获得:

其中,N 是模态阶数。
三、程序设计
蒸汽发生器传热管流致振动线性分析程序主要包括三个功能,分别是:模态分析、流弹不稳定性分析和湍流激振响应计算,具体功能结构图如图1所示。
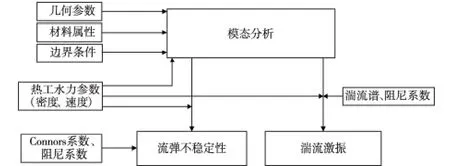
图1 程序功能结构图

图2 程序总体架构设计图
根据上述蒸汽发生器传热管流致振动线性分析程序的数学模型以及功能结构图,对程序的总体架构进行设计,如图2所示。程序共创建了5个数据类,3个模型分析计算类及1个抽象类。其中,模态分析计算类的数据属性依赖于边界条件、几何参数、材料属性和热工水力参数,计算结果返回模态参数;基础模型属于抽象类,其数据属性依赖于模态参数和热工水力参数;流弹不稳定性和湍流激振是由基础模型派生。自主开发程序的核心计算代码采用C + + 编写,运行环境为Linux 操作系统。

图3 传热管的几何结构示意图

图4 一次侧流体密度

图5 二次侧流体密度

图6 二次侧流体的横向速度
四、算例验证
为了验证自主开发程序的正确性,本文对某型号蒸汽发生器某根传热管进行流致振动分析,将计算结果与国外专用软件的计算结果进行对比。传热管的详细设计参数为:管外径19.05m;管壁厚1.09 ×1013m;传热管密度8091kg/m3;杨氏模量Pa;泊松比0.3;弯管处的弯曲半径260.585 ×1013m;与该传热管接触的防振条数目为1;支撑板间距为1.094m,共9 块支撑板;传热管间距为m;管板到第一块支撑板的距离为1.094 m;弯管中心到第9 块支撑板的距离为0.088m;传热管直管段总长度为9.934m。蒸汽发生器传热管的几何结构示意图如图3所示。传热管的一次侧流体密度、二次侧流体密度和二次侧流体横向速度分别如图4、图5 和图6所示。
从表1 和表2 中可以看出,本文对流弹不稳定率和湍流激振响应的计算结果与国外专用软件相应的计算结果非常吻合,最大相对误差不超过0.2%,足以说明本文的计算结果足够准确可靠,完全可以替代国外软件来进行蒸汽发生器传热管流致振动的线性分析计算,可以在不涉及知识产权的前提下对管束的流弹不稳定性和湍流激振进行评估,为蒸汽发生器的设计提供指导。

表1 流弹不稳定率的计算结果对比
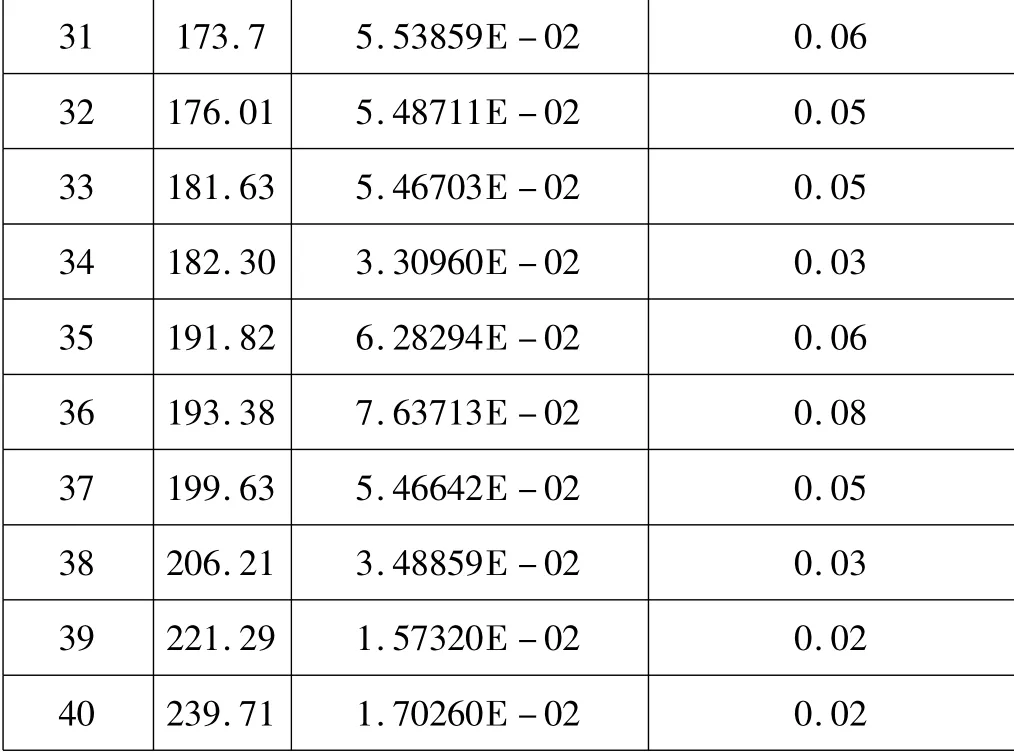
31 173.7 5.53859E-02 0.06 32 176.01 5.48711E-02 0.05 33 181.63 5.46703E-02 0.05 34 182.30 3.30960E-02 0.03 35 191.82 6.28294E-02 0.06 36 193.38 7.63713E-02 0.08 37 199.63 5.46642E-02 0.05 38 206.21 3.48859E-02 0.03 39 221.29 1.57320E-02 0.02 40 239.71 1.70260E-02 0.02

表2 湍流激振响应的计算结果对比
五、结语
根据蒸汽发生器传热管流致振动线性分析的数学模型,采用模态叠加法对流致振动响应进行分析计算。采用面向对象思想对自主开发程序进行总体架构设计,核心计算代码采用C ++编写,使得程序具有可阅读性、可扩展性和可维护性。通过程序计算结果与国外专用计算软件进行比较,表明本文总结的蒸汽发生器传热管流致振动线性分析的数学模型和计算方法具有可靠性,该程序适用于对蒸汽发生器传热管的流弹不稳定性和湍流激振进行评估。目前,该自主开发的线性分析程序是一个测试版本,需要进一步的完善和全方位的检验,且非线性分析程序正在研发中。
[1]Au-Yang M K. Flow-induced vibration of power and process plant components[M].New York:AMSE Press,2001
[2]丁训慎.蒸汽发生器传热管的微振磨损及其防护[J]. 核安全,2006
[3]丁训慎.核电厂蒸汽发生器设计中的安全问题[J].核安全,2005
[4]蒋庆磊,乐适,王永,等.蒸汽发生器传热管面内流体弹性失稳分析[J].核安全,2014
[5]韩同行,左超平,秦加明,等.蒸汽发生器传热管流弹失稳计算[J].设计计算,2014
[6]朱勇,秦加明,任红兵,等. 基于ANSYS 的蒸汽发生器传热管流致振动分析程序[J].核动力工程,2014
[7]F.AXISA,J.ANTUNES,B.VILLARD and M.WULLSLEGER.Random excitation of heat exchanger tubes by cross-flow 1988 International. symposium on flow -induced vibration and noise[A].ASME Winter Annual Meeting[C].1988,11,27~12,2
[8]E. DELANGRE,B. BEAUFILS,J. ANTUNES. The numerical prediction of vibrations in tube bundles induced by cross -flow turbulence. Vth International Conference on flow - induced vibrations[J]. Brighton,1991,5
