平面度误差评定的几种方法

2015-01-23吴呼玲

产业与科技论坛 2015年22期

□吴呼玲

目前，对平面度误差评定常用的方法有:对角线法，任意三点法，最小包容区域法三种。对角线法是学生在平面度误差检测中常用的方法;最小包容区域法是课堂上教师讲授的主要评定平面度的方法;任意三点法是不常用的方法。在实际的教学中，课堂的理论教学与实际评定的方法不吻合。本文提出几种不同的平面度误差处理方法，以及处理结果。

一、平面度误差的评定方法

(一)对角线法评定平面度误差。对角线法评定平面度误差的判断依据就是将被检测的物质表面的一条对角线作为被测表面，并且将与另一条对角线平行的作为评定的基准面，这样就会得出对平面度误差值的确定，即以平行基准面其距离最小的平面间距离。

(二)三远点法评定平面度误差。三远点法:是以通过实际被测表面上相距最远，而且这些评定基面都不能在一条直线上，这样一来平行与基面，并且距离最小的平面间就是平面度误差值。

(三)最小区域法评定平面度误差［1］。最小区域法就是以实际被测表面区域的宽度作为误差值，该方法是目前应用比较广泛的一种方法。

1．三角形准则。由两平行平面包容被测面时，两平行平面与被测面接触点分别为3个等值最高(低)点与1个最低(高)点，且最低(高)点的投影落在由3个等值最高(低)点所组成的三角形之内，如图1所示。

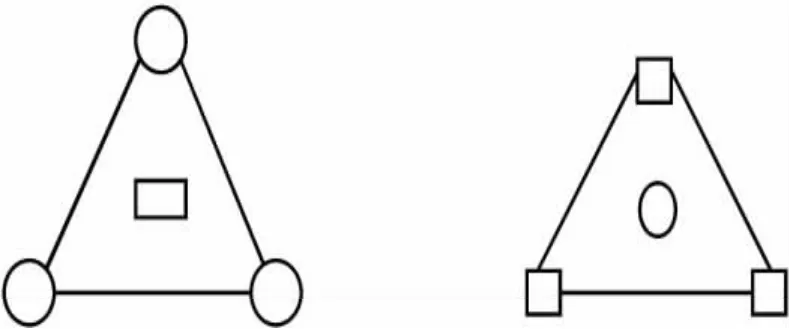
图1 三角形准则

2．交叉准则。由两平行平面包容被测面时，两平行平面与被测面接触点分别为两个等值最高点与两个等值最低点，且最高点连线的投影与最低点连线相互交叉，如图2所示。

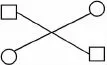
图2 交叉准则

图3 直线准则

3．直线准则。由两平行平面包容被测面时，两平行平面与被测面接触点分别为两个等值最高(低)点与一个最低(高)点，且一个最低(高)点的投影位于两等值最高(低)点的连线上，如图3所示。

二、三种方法评定平面度误差的数据处理方法

在某基准平面上，用千分表测量一块400(mm)×400(mm)平板的平面度误差，测得数据如图所示，求出其平面度误差。

平面度误差评定方法的数据处理采用旋转变换理论［2］，如表1所示。

表1 旋转变换理论

(一)用对角线法评定平面度误差时的数据处理。对角线法评定平面度误差的方法是，将通过被测平面的一条对角线且平行另一条对角线作为基准平面，以此基准面为基准，平面度误差为被测实际表面偏离基准平面的最大偏离量，如表1所示，即公式(1):

求解得:P= -6;Q=2

求解得:p= -5;Q= -1

求解得:p= +2;Q= +5

将实际被测表面旋转到与基准平面平行后，各点测得数据如表2所示。以包容被测平面上0～0对角线，且平行于(-6)～(-6)对角线作为基准平面，实际被测表面偏离基准平面的最大值为+16，最小值为-19。因此，该平面的平面度误差为实际被测表面偏离基准平面的最大值与最小值之差，即+16 -(-19)=35μm。

(二)三远点法评定平面度误差时的数据处理。三远点法是在被测平面上选取最远且不在同一直线上的三点作为基准平面，以此基准面为基准，平面度误差为被测实际表面偏离基准平面的最大偏离量。如表1 可见，即公式(2)。

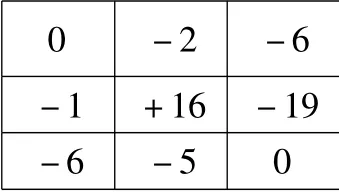
表2 对角线法各测点数据图

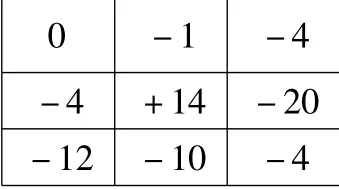
表3 三远点法各测点数据图

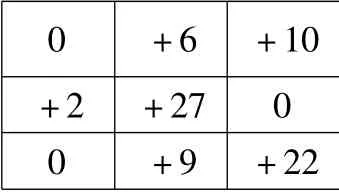
表4 最小区域法各测点数据

将实际被测表面旋转到与基准平面平行后，各点测得数据如表3所示。以-4，-4，-4 三点作为基准平面，实际被测表面偏离基准平面的最大值为+14，最小值为-20。因此，该平面的平面度误差为实际被测表面偏离基准平面的最大值与最小值之差，即+14 -(-20)=34μm。

(三)最小区域法评定平面度误差时的数据处理。最小包容区域法是仔细观察所测数据的分布情况，分析数据分布符合最小区域法中的三角形准则、交叉准则和直线准则中的哪一种。然后选择基准平面，平面度误差为被测实际表面偏离基准平面的最大偏离量。如表3所示，该测量数据符合三角形准则，其中+20 为最高点，-10，-9 和0 为最低点，组成三个低点形成的三角形中包容一个高点的情况。如表1 可见，即公式(3)。

将实际被测表面旋转到与基准平面平行后，各点测得数据如表4所示。以0，0，0 三点作为基准平面，实际被测表面偏离基准平面的最大值为+20，最小值为0。因此，该平面的平面度误差为实际被测表面偏离基准平面的最大值与最小值之差，即+20 -0 =20μm。