竖直壁面贴附式送风模式气流组织特性研究

尹海国，李安桂

（西安建筑科技大学环境与市政工程学院，陕西 西安 710055）

建筑通风空调系统中，目前主要的送风模式有混合通风和置换通风两种[1]．相比较来说，置换通风具有送风效率高、室内空气品质优、人员舒适性强的优点[2-3]．但是，传统置换通风散流器大多位于房间下部，送风直接进入工作区，为了避免产生吹风感，送风速度往往受到限制，因此只能承担40-50 W/m2左右的室内负荷[4]，作用能力有限．并且系统布置时往往需要升高楼板高度(可达30 cm以上，布置下送管道)，占用建筑下部有效空间．

为解决上述两种传统送风模式存在的问题，专家学者们提出了一系列新型的送风模式．例如，2000年Karimipanah等人[5]提出基于半圆形或矩形送风口的竖直壁面贴附式冲击射流通风（Down-to-floor Impinging Ventilation, DIV）；2002年，Melikov等人[6]针对局部环境控制提出的个性化通风(Personalized Ventilation, PV)；2008年，林章等人[7]基于节能考虑提出高温空调层式通风(Stratum Ventilation, SV)；2014年，曹广宇等人[8]针对工作区区域环境分隔与控制提出的工作区保护通风(Protected Occupied zone Ventilation, POV)等．

本文提出的竖直壁面贴附式送风模式[9]也属于新型送风模式的一种，但与上述送风模式在作用原理上存在一定不同，它兼具混合通风和置换通风的特性．同时，竖直壁面贴附式送风模式既有混合通风送风口容易布置、不占用工作区有效空间之优点，又具备置换式通风室内空气品质高、能源消耗较小之优点，能够在一定程度上解决现有送风模式存在的弊端[10]．

1 竖直壁面贴附式送风理论模型

竖直壁面贴附式送风模式理论基础基于壁面贴附送风和冲击式射流，但与实际工程中主要应用的顶板水平贴附送风不同，竖直壁面贴附式送风是沿竖直壁面的空气流动，流动方向与重力方向一致，因此送风轴线速度衰减相对较慢，进而影响冲击转向后水平向的气流组织特性．而与主要采用圆孔或矩形风口的传统冲击射流不同，本文研究的竖直壁面贴附式送风采用长宽比较大的条缝风口，并且考虑到风口安装要求，条缝风口中心距贴附侧墙有一定的距离 s，因此送风在沿侧墙向下运动冲击角落之前首先要偏转并与墙壁形成贴附，这些改变可能会对气流组织特性产生影响．

图1(a)是竖直壁面贴附式送风模式气流组织理论模型示意图．由图可知，该送风模式气流组织可以划分为竖直向贴附区，射流冲击偏转区和水平向空气湖区3个部分．由于送风口与竖直墙壁间存在一定距离，而在康达效应的作用，竖直向贴附区内将会存在一定的偏转段．该气流组织模型得到了全尺寸可视化实验验证．从图1(b)中清晰地看出，射流主体能够向侧墙偏转，依次与竖直壁面和地板形成贴附流动，并在人员工作区形成空气湖状速度分布．同时由于贴附壁面的存在，送风主体进入工作区前并未与室内空气产生较多的混合．这表明竖直壁面贴附式送风模式在某种程度上确实具备了置换送风的一些优点．

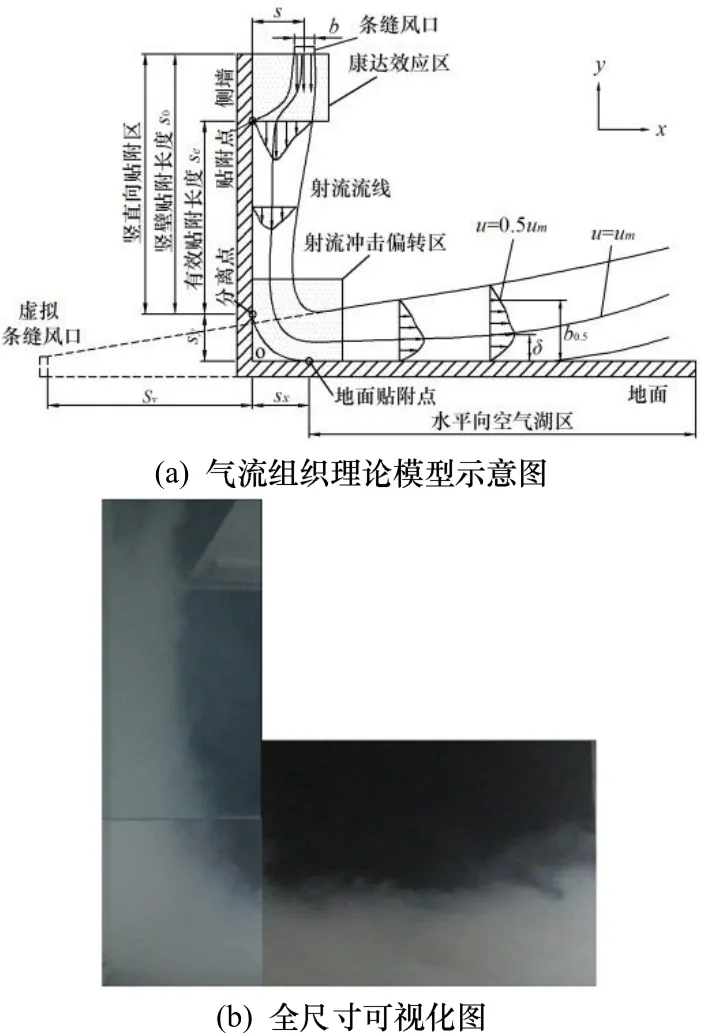
图1 竖直壁面贴附式送风模式图Fig. 1 The air distribution model of attached air curtain ventilation

2 竖直壁面贴附式送风全尺寸实验

基于竖直壁面贴附式送风理论模型，建立了1:1全尺寸实验装置．通过竖直向贴附区和水平向空气湖区速度场的三维定量测试数据，来获得竖直壁面贴附式送风模式轴线速度、沿风口长度方向平均速度和送风主体断面速度分布的特性，以及送风沿运动方向厚度的扩展特性，为这种新型气流组织的设计及工程应用提供数据基础．

2.1 全尺寸实验装置及测点布置

图2为全尺寸实验装置及测点布置示意图，实验室尺寸为 5.4×7.0×3.16 m3(长×宽×高)，条缝风口均匀送风用静压箱装置[11]尺寸为2.5×0.5×0.5 m3(长×宽×高)．条缝风口距贴附墙面垂直距离s为0.1 m、距地面垂直距离h为2.6 m，条缝出风口断面长度l为2.0 m、宽度b为0.05 m．送风采用离心式风机，额定风量1 000 m3/h，送风量由节流阀控制，实验送风速度取1.0、1.5和2.0 m/s．

竖直向贴附区y方向轴线速度测试采用非均匀布点，共11个测点、测量范围2.45 ～ 0.25 m；z方向平均速度测试采用均匀布点，共 10个、测量范围−1.9 ～ 1.9 m；x方向断面速度测试采用均匀布点，共10个、测量范围0.04 ～ 0.40 m．水平向空气湖区x方向轴线速度测试采用非均匀布点，共12个测点、测量范围0.35 ～ 4.4 m；z方向平均速度测试采用均匀布点，共10个、测量范围-1.9 ～ 1.9 m；y方向断面速度测试采用均匀布点，共10个、测量范围0.04～ 0.40 m．

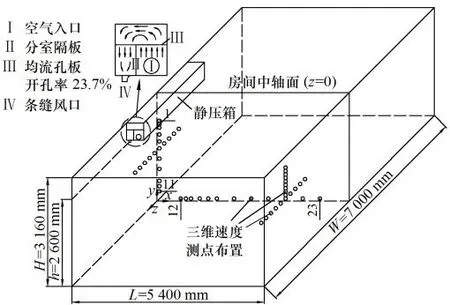
图2 竖直壁面贴附式送风全尺寸实验装置及三维速度测点布置Fig. 2 Full scale experimental model and measurement points distribution of attached air curtain ventilation

2.2 测试仪器及精度

速度场三维测试选用SWA03/31风速探头配合Swema多点测试采集系统(最多可控制16个测点同时测量)，以实现速度场的多点实时无扰动监测．对于每个测点的速度测试，采样频率设置为5 Hz，采样周期设置为180 s，以消除送风脉动性对测试结果准确性的影响[12]．速度场三维测试所用测试仪器及精度见表1，测量时所用SWA 03/31风速探头刚经过厂家标定，标定结果显示，用于速度场三维测试的 SWA 03探头在本文速度测试范围内(0.07～2.0 m/s)最高误差为0.012 m/s，用于送风系统送风量测试的 SWA 31探头在本文速度测试范围内(2.5～5.0 m/s)最高误差为0.1 m/s，仪器精度符合测试要求．

表1 实验测试仪器及精度表Tab. 1 Experimental equipments and instrument precision

3 实验结果及对比分析

3.1 轴线速度衰减

图3为测试得到的竖直向贴附区和水平向空气湖区轴线速度分布，及与类似送风模式已有研究结论的对比情况．轴线速度对比对象分别是基于水平壁面贴附送风的Rajaratnam[13]计算式、ASHRAE[14]计算式，基于多股喷嘴汇合式竖直壁面贴附送风的Cho等人[15]计算式，基于矩形风口竖直壁面贴附冲击式送风的 Karimipanah等人[16]计算式，和采用Cao[17]虚拟原点理论推导得到的条缝风口竖直壁面贴附式送风计算式(虚拟原点理论见图1a)．

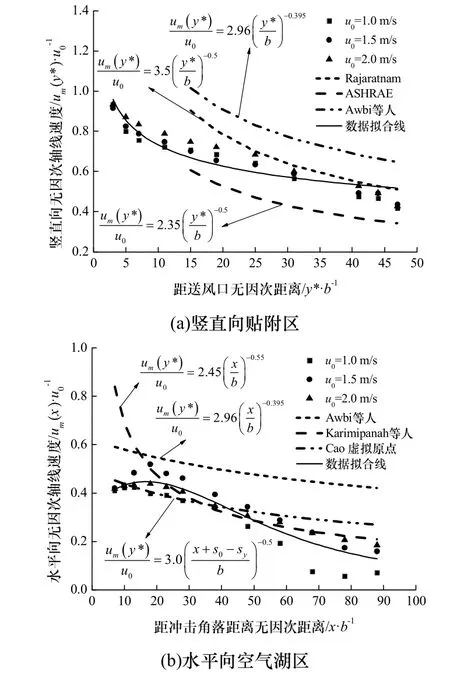
图3 不同送风速度下无因次轴线速度分布及对比图Fig. 3 Non-dimensional maximum velocity decay and comparison under different air supply velocities

由图3a可知，竖直向贴附区，送风速度变化对竖直向贴附区轴线速度分布影响不大，轴线速度均随流动距离的增加而呈现一致的衰减规律．与其他人员的研究结论相比，Rajaratnam计算式能够较为准确的预测本文送风模式竖直向贴附区充分发展段的轴线速度，但对应测点处计算值偏高．ASHRAE计算式对应测点处计算值偏低，但在衰减规律方面与实验数据一致，因此综合考虑两个既有的计算式，本文送风模式竖直向贴附区轴线速度计算式可以表述为式(1)的修正形式．Cho等人轴线速度计算式总体衰减规律与全尺寸实验数据一致，但对应取值点处轴线速度数值较高，这是因为圆形喷嘴相对于矩形和线形送风口来说，速度衰减相对较慢，因此对于竖直壁面贴附式送风模式，为了提高送风主体的延伸扩散能力，可以考虑将条缝风口改为平行布置的喷嘴组合，但同时要考虑吹风感的有效消除．

式中：um(y*)为距送风口距离为 y*时的轴线速度，y*为房间高度h和y*对应高度y的差值(y*=h-y)，u0为送风速度，b为条缝风口宽度．

图3b表明，水平向空气湖区轴线速度分布与竖直区类似，送风速度对轴线速度分布影响不大．不同送风速度下，射流主体冲击角落偏转后，沿运动方向约1 m长度范围内(x/b≤20)轴线速度数值均有一定的增加，而后随流动距离的增加又逐渐衰减．测试数据与计算式对比，Cho、Karimipanah等人提出的计算式及Cao虚拟原点理论推导得到的半经验公式均不能预测加速段的存在，但基于Giddings方程的式(2)能够非常精准的预测这一现象．如果不考虑加速段的影响，基于 Karimipanah等人矩形风口改进的用于条缝风口水平向轴线速度的计算式与全尺寸实验数据吻合较好，可用于竖直壁面贴附式送风模式水平区轴线速度的预测．

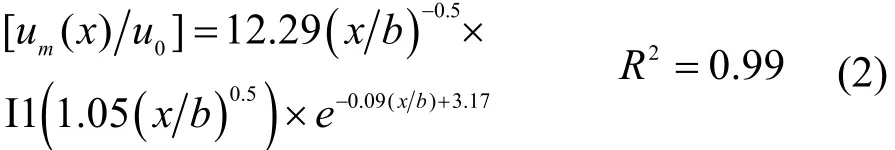
式中：um(x)为送风主体转弯后距冲击角落距离为 x时的轴线速度，I1()为一阶修正的贝塞尔函数．

同时由图3可知，与传统置换通风相比，竖直壁面贴附式送风主体进入工作前速度衰减了一半以上，但在贴附壁面的“挟持作用”下，送风并未与工作区之外的空气有较多混合，因此进入工作区的空气保持了送风主体的绝大部分冷/热量和新鲜度．轴线速度的衰减主要是因为送风主体面积的扩大，相当于在房间左下角落处形成了一个虚拟的扩张式送风口，在将足够的能量送入工作区的同时，由于送风断面的增加，降低了工作区的平均风速，避免了吹风感的产生，一定程度上解决了置换通风存在的弊病．

3.2 沿风口长度方向平均速度分布

Főrthman[18]指出送风口长宽比大于20:1时，三维送风可以忽略侧墙的影响而简化为二维送风，本文将对长宽比为40:1的条缝风口进行全尺寸实验，以验证和分析条缝风口竖直壁面贴附式送风的二维特性．

由图4可知，沿送风流动方向不同位置处，风口长度方向 10个测点的平均速度分布规律与轴线速度一致，两种速度对应取值点数值大小近似相等．因此条缝风口形成的三维竖直壁面贴附式送风模式具有较好的二维特性，研究时可以忽略风口长度这一维度的影响．

3.3 送风主体断面速度分布

为分析条缝风口距贴附墙面存在一定距离 s时，本文送风模式是否能够近似为全程贴附送风，同时验证 Verhoff[19]和 Schwarz等人[20]提出的用于水平向送风主体断面速度分布计算式在本文送风模式下的适用性，采用全尺寸实验数据与现有计算式进行对比分析如下图5．

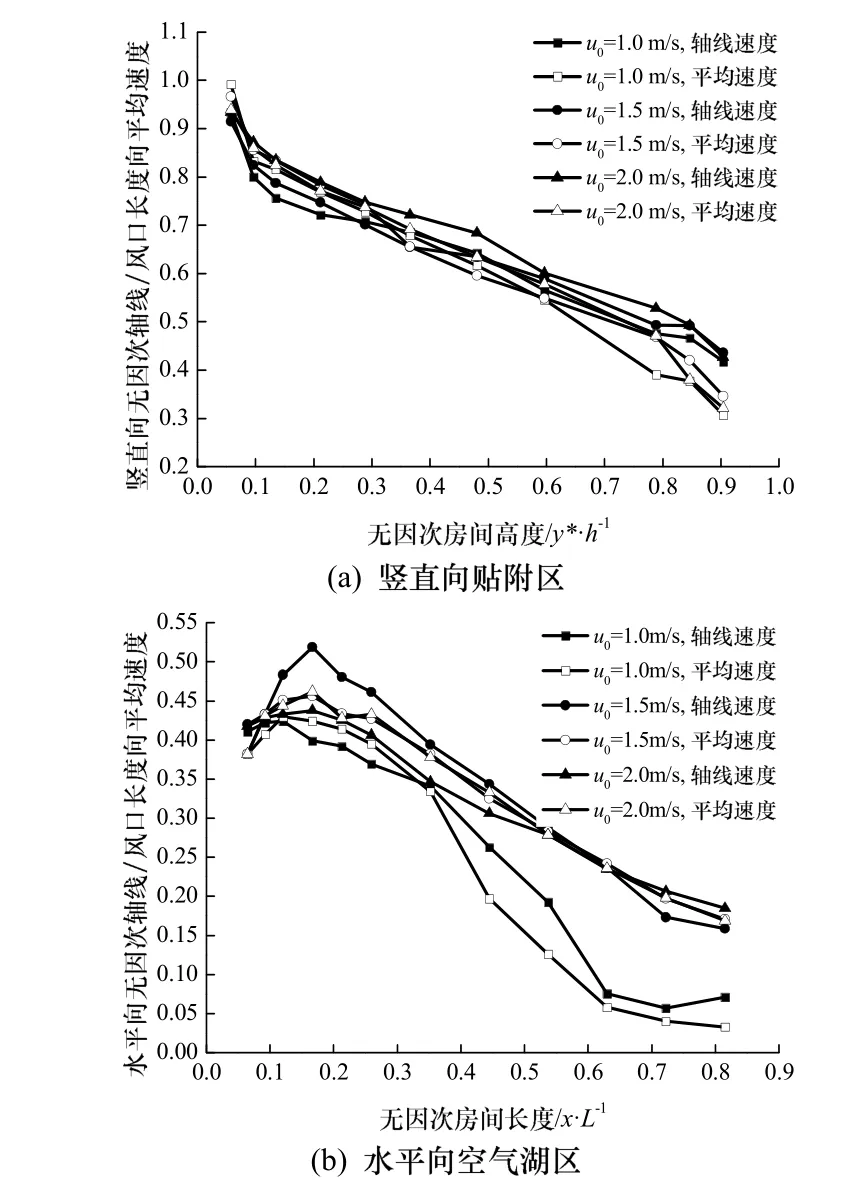
图4 不同送风速度下无因次轴线/平均速度分布对比图Fig. 4 Comparison of non-dimensional maximum velocity and average velocity under different air supply velocities

图5 不同送风速度下无因次断面速度分布图Fig. 5 Non-dimensional velocity profiles distribution under different air supply velocities

由图5a可知，竖直向贴附区，沿送风运动方向不同断面速度分布具有相似性，送风能够在较短距离内即与竖直壁面形成贴附，y=2.45 m处断面速度分布已经具有了与主体段一致的相似性，因此虽然条缝风口中心与贴附墙面间存在 0.1 m的垂直距离，但送风能够忽略这一影响，近似按照全程贴附送风来研究．图 5b表示的水平向空气湖区与竖直区类似，全尺寸实验测试数据与Verhoff和Schwarz等人计算式吻合较好．相比来说，竖直向贴附区Schwarz计算式在断面速度分布计算方面精度较高，而水平向空气湖区则是Verhoff计算式较高．

3.4 送风沿运动方向厚度扩展

图6是全尺寸实验测试得到的送风沿运动方向厚度扩展及与Rajaratnam[13]给出的水平壁面贴附送风、Beltaos[21]给出的冲击射流竖直区和水平区计算式的对比．

由图6可知，竖直向贴附区，不同风速下实验得到的厚度扩展规律及对应取值点数值大致类似，沿送风主体运动方向厚度b0.5线性增大，数据可以拟合得到式(3)的厚度扩展计算式，扩展率为0.093．与Rajaratnam水平壁面贴附射流0.068的扩展率相比，竖直壁面贴附式送风沿运动方向厚度扩展率较大，约为水平射流的1.37倍，这主要是因为水平壁面贴附送风厚度扩展方向与重力加速度方向相反；实验数据与 Beltaos冲击射流竖直向扩展率近似一致，两者相差仅 7%，因此竖直壁面贴附式送风可作为冲击射流的一半来考虑．

水平向不同风速下，实验得到的送风主体厚度扩展仍呈现一定的线性分布规律，但由于送风冲击角落后加速段的存在，主体厚度呈现先收缩后扩展的分布形态，收缩段和扩展段的数据分别拟合得到式(4)的厚度收缩计算式和式(5)的厚度扩展计算式．扩展段扩展率为0.082，与Rajaratnam水平壁面贴附射流扩展率相比，射流冲击角落转向后扩展率增大了约1.21倍；而与Beltaos冲击射流水平向扩展率近似一致，两者相差仍为 7%．所以竖直壁面贴附式送风可以近似按冲击射流理论来描述．

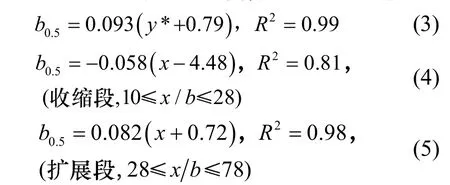
式中：b0.5为送风主体特性半厚度，是流速等于0.5um所在位置距轴线的距离．

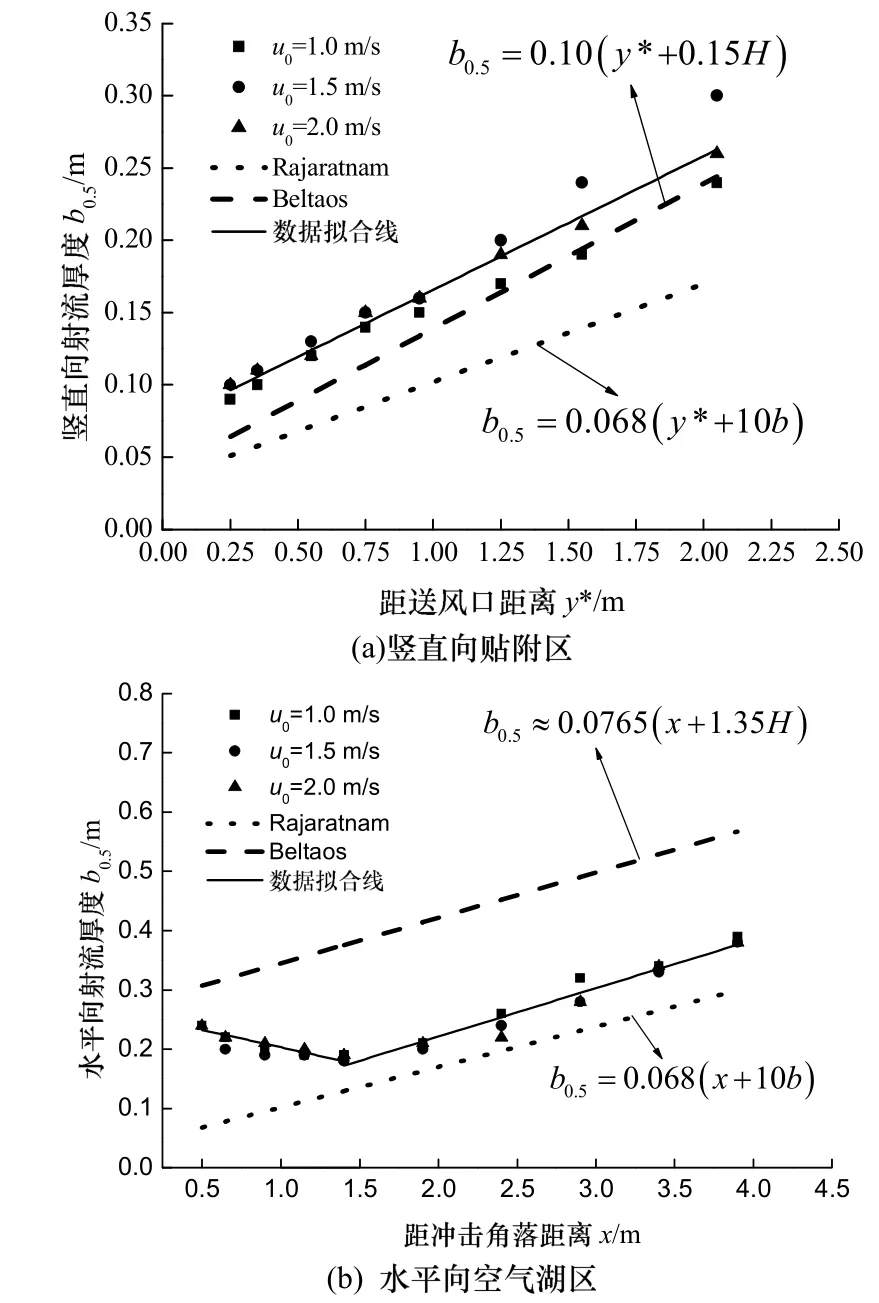
图6 不同送风速度下送风主体厚度扩展图Fig. 6 Extending in thickness of air supply body under different air supply velocities

4 结语

采用全尺寸实验的方法对竖直壁面贴附式送风这一新型模式的气流组织特性进行了全面研究，并与国内外已有研究结论进行了对比分析，研究表明：

(1) 竖直壁面贴附式送风能够在工作区形成类似于置换通风的空气湖状速度分布，并能有效解决置换通风制冷能力低、占用工作区下部有效空间等弊病．

(2) 基于国内外射流领域已有理论及经验公式，得到了竖直向贴附区和水平向空气湖区送风轴线速度衰减、送风主体断面速度分布和送风沿运动方向厚度扩展的计算式．

(3) 采用长宽比40:1的条缝风口的竖直壁面贴附式送风具体一定的二维特性，对送风主体特性研究时沿条缝风口长度方向取任意截面均可．

(4) 条缝风口中心距贴附墙面距离小于 0.1 m时，并不会对气流组织特性产生影响，送风可以按照全程贴附送风模式来研究．并且此时可以基于镜面原理，将竖直壁面贴附式送风当做冲击射流的一半来考虑．

References

[1] ASHRAE. 2001 ASHRAE Handbook: Fundamentals[M].Atlanta: American Society of Heating, Refrigeration and Air-Conditioning Engineers, Inc., 2001: 26.2-26.3.

[2] 马仁民. 置换通风的通风效率及其微热环境评价[J].暖通空调, 1997, 27(4): 1-6.MA Renmin. Displacement ventilation effectiveness and evaluation of the micro thermal environment[J]. Heating Ventilating & Air Conditioning, 1997, 27(4): 1-6.

[3] 李强民. 置换通风原理、设计及应用[J]. 暖通空调,2000, 30(5): 41-46.LI Qiangmin. Displacement ventilation: principles, design and applications[J]. Heating Ventilating & Air Conditioning, 2000, 30(5): 41-46.

[4] HAMILTON S, ROTH K W, BRODRICK J. Displacement ventilation[J]. ASHRAE Journal, 2004, 46(9):56-58.

[5] KARIMIPANAH T, SANDBERG M, AWBI H B. A comparative study of different air distribution systems in a classroom[C]//Proceedings of the ROOMVENT 2000,Reading, UK, 2000, Vol. II: 1013-1018.

[6] MELIKOV A K, RADIM C, MILAN M. Personalized ventilation: evaluation of different air terminal devices[J].Energy and Building, 2002, 34(8): 829-836.

[7] 林章, 周天泰, 曾志宽. 层式通风—高温空调下的出路[J]. 化工学报, 2008, 59(S2): 235-241.LIN Zhang, CHOW T T, TSANG C. Ventilation system for higher room temperature setting[J]. Journal of Chemical Industry and Engineering, 2008, 59(S2): 235-241.

[8] CAO G Y, SIRÉN K, KILPELÄINEN S. Modelling and experimental study of performance of the protected occupied zone ventilation[J]. Energy and Building, 2014,68(Part A): 515-531.

[9] 李安桂, 邱少辉, 王国栋. 竖壁贴附射流空气湖模式通风系统:中国, 200810017349.0 [P]. 2008-01-21.LI Angui, QIU Shaohui, WANG Guodong. A downward directed vertical wall jet ventilation system based on air lake model: China, 200810017349.0 [P]. 2008-01-21.

[10] LI Angui, YIN Haiguo, ZHANG Wangda. A novel air distribution method-Principles of air curtain ventilation[J].International Journal of Ventilation, 2012,10(4): 383-390.

[11] 李安桂, 尹海国, 陶鹏飞. 一种出风均匀且风口可调式静压箱[P]. 中国, 201010549210.8, 2012.07.25.LI Angui, YIN Haiguo TAO Pengfei. A plenum chamber with uniform air supply and adjustable air outlet[P]. P.R.China, 201010549210.8, 2012.07.25.

[12] THORSHAUGE J. Air-velocity fluctuations in the occupied zone of ventilated spaces[J], ASHRAE Transactions,1982, 88(2): 753-764.

[13] RAJARATNAM N. Turbulent Jets[M]. Amsterdam:Elsevier, 1976: 211-213.

[14] ASHRAE. 1993 ASHRAE Handbook: Fundamentals[M].Atlanta: American Society of Heating, Refrigeration and Air-Conditioning Engineers, Inc., 1993.

[15] CHO Y J, AWBI H B, KARIMIPANAH T. Theoretical and experimental investigation of wall confluent jets ventilation and comparison with wall displacement ventilation[J]. Building and Environment, 2008, 43(6):1091-1100.

[16] KARIMIPANAH T, AWBI H B. Theoretical and experimental investigation of impinging jet ventilation and comparison with wall displacement ventilation[J]. Building and Environment, 2002, 37(12): 1329-1342.

[17] CAO G. Modelling the attached plane jet in a room[D].PhD thesis, Finland: Helsinki University of Technology,2009.

[18] FŐRTHMANN E. Turbulent jet expansion[R]. Washington, D.C.: National Aeronautics and Space Administration, 1934: No. TM-789.

[19] VERHOFF A. The two-dimensional turbulent wall jet without an external free stream[R]. Princeton: Princeton University, 1963: No. 626.

[20] SCHWARZ W H, COSART W P. The two-dimensional turbulent wall jet[J]. Journal of Fluid Mechanics, 1961,10(4): 481-495.

[21] BELTAOS S, RAJARATNAM N. Plane turbulent impinging jets[J]. Journal of Hydraulic Research, 1973,11(1): 29-59.