基于模糊可靠性的盘式制动系统故障树的分析

陈志伟，王雷刚，陈 佑

（中国矿业大学（北京） 机电与信息工程学院，北京 100083）

0 引言

矿井提升是被喻为矿井的咽喉，其安全性可靠性直接影响着矿山生产人员的生命安全和矿井生产能力。而矿井提升机的制动系统是其安全运行的重要保障。提升机制动系统的作用是： ①正常工作制动；②正常停车制动；③安全制动；④调绳制动[1]。国家对矿井提升及其制动系统的安全问题极为重视，《煤矿安全规程》和《煤矿机电设备完好标准》都对其安全做出了明确规定。

安全可靠的制动系统不仅可以减少提升设备的维修量，降低维修成本，延长设备使用寿命，更重要的是能够防止和杜绝设备故障、事故的发生。制动器的可靠性是矿井提升机的日常使用、维护、管理的重要内容[2]。

1 盘式制动系统的可靠性概述

可靠性的定义是，产品在规定的条件下和规定的时间内完成规定功能的能力。可靠性理论的研究核心主要是对象、规定条件、规定时间、规定功能和概率这五个因素。其中概率是可靠性研究的关键，把可靠性用概率这一具体的数学形式表示，是可靠性技术发展的出发点，也是可靠性数量化的标志[3]。本文即是围绕以上几个因素在规定的条件下，讨论矿井提升机的制动系统在不同时期能完成其规定功能的概率。

可靠性特征量是对系统可靠性进行定量化的最为有力的数学工具和分析基础。可靠性特征量的真实值在理论上是唯一的，但在实际中是很难求得的。我们通常会用一个基于数理统计的特征量估计值来估算其真值。特征量估计值的得出是盘式制动系统可靠性分析的难点，因为在实际生产中盘式制动系统的失效数据采样比较困难：每一台矿井提升机的工作环境都各不相同，所以各个盘式制动系统之间没有横向的数据可以借用，对其可靠性特征量的提取只能依托漫长的时间轴在其本身的纵向数据中获得。

可靠度多个可靠性特征量中最重要的。盘式制动系统属于可修复产品，它的可靠度估计值是： 故障间隔工作时间达到或超过规定时间的次数与观察时间内正常工作的总次数的比值。

2 盘式制动器的工作原理及其故障树

目前，国内外提升机大多采用盘式制动系统。盘式制动器结构紧凑重量轻，并且动作灵敏安全性好。《煤矿安全规程》 对盘式制动提出了严格的要求： ①对于立井或倾角大于30°的斜井最大制动力矩不得小于提升或下放最大静负荷力的3 倍；②对于双滚筒提升机，为了使离合器打开时能制住游动滚筒，制动器在一个滚筒上的制动力矩，不得小于该滚筒悬挂提升容器和钢丝绳重力所产生的力矩的1.2 倍；③安全制动必须能自动、迅速和可靠地实现，制动器的空动时间不得超过0.3 秒[4]。

盘式制动器的工作原理如图1 所示。当液压缸内油压为pA最小时，制动盘受最大正压力FN的作用，呈全制动状态；当油压pA升高时，液压油产生的推力F1增大，弹簧力F2将部分地被克服，对制动盘的作用力减小，从而减小制动力矩；当工作油压升高，使F1＞F2时，则完全解除制动，FN=0[1]。

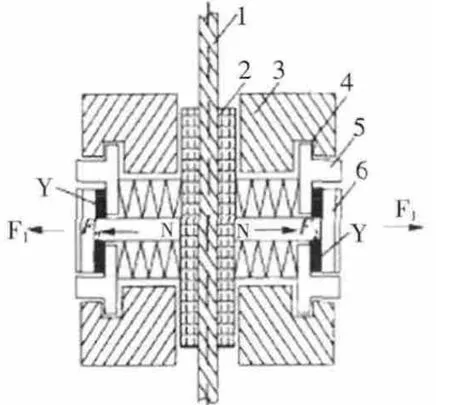
图1 盘式制动器工作原理图Fig.1 Schematic of mining hoister braking system

作为选择和校核计算，盘式制动器的两个最重要的工作参数是制动器所需产生的正压力和工作油压。根据制动力矩条件“所产生的力矩与实际提升最大静荷重旋转力矩之比K 值不得小于3”可得：

式中： MZ—制动力矩；Q—一次提升货载质量；n1—主绳根数；p—每根主绳单位长度重力；n2—尾绳根数；q—每根尾绳单位长度的重力；H—提升高度；R—提升机卷筒半径。这些参数都是由矿井及矿井提升机的实际情况所确定的，其中MZ—盘式制动器制动力矩的下限。制动状态下，每个闸瓦对制动盘的正压力FN需要满足的条件是：

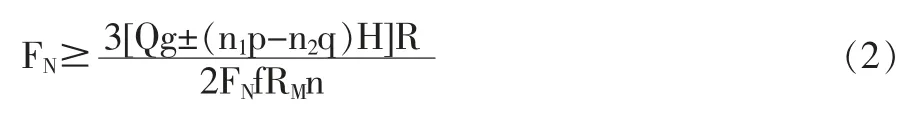
式中： FN—作用于制动盘上的正压力；f—闸瓦与制动盘之间的摩擦因数；RM—制动盘平均摩擦半径；n—制动器副数。以上是对正压力的推导，在松闸时液压油对活塞的压力及压强可以推出为：

式中： F1—制动油缸中液压油产生的压力；K—一片碟形弹簧的刚度n' 代表碟形弹簧的片数；pC—制动器所需油压和背压之差；D 和d 分别代表液压缸直径和活塞杆直径。所以实际工作压力可以表示为p=pC+p背，其中p背是液压系统在制动状态存在的背压。

由以上推导可知，影响盘式制动系统的参数有弹簧正压力、闸瓦间隙、制动油压强、制动盘的偏摆、制动器的空动时间以及闸瓦的温度和制动油的温度等。现在建立故障树如图2 所示。

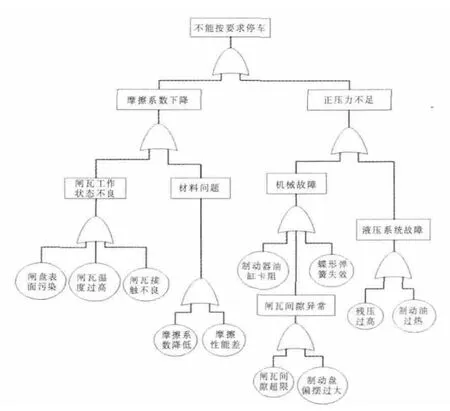
图2 盘式制动系统制动失效的故障树Fig.2 Fault tree of mining hoister braking system

3 对盘式制动系统故障树的分析

系统的可靠性分为固有可靠性和和使用可靠性。使用可靠性取决于产品的使用条件和维护条件。盘式制动系统的维护任务主要是对其制动盘的维护： 制动盘两侧的洁净程度；在制动时制动闸瓦同制动盘的接触面积；制动盘表面的磨损程度。固有可靠性是产品内在的可靠性，需要通过分析求得。盘式制动器在总体上属于串联系统，串联系统对可靠性的要求相对较高。串联系统的每一个环节出现问题，都会导致系统的失效。基于经典可靠性理论的故障树分析将故障树顶事件和底事件的可靠度视为一个准确固定的数值，这其实不符合实际情况的。其原因是精确的概率化需要依托大量的数据供统计，而在盘式制动系统中，故障发生的频率很低，无法获取大量的数据，并且在复杂的人机系统中，由于人的因素成系统建模的不精确，不宜用纯概率的方法。

没有充足的样本采样来完成分析是对盘式制动系统可靠性分析的瓶颈。并且对于矿井提升机制动系统，我们是不希望有大量失效数据产生的，因为这意味着事故，意味着经济损失甚至人员伤亡。这就形成了一个自相矛盾的悖论。为解决这一矛盾，本文引入模糊可靠性和模糊故障树的分析方法，利用相对不充分的数据，依托模糊数学理论来描述提升机制动系统的失效情况。采用模糊数来描述事件发生的概率，既能结合工程技术人员的实际经验和判断来构造模糊数的隶属函数，从而较为准确地描述出故障事件的概率，同时能在一定程度上允许由描述的误差，因此它具有较大的灵活性和适应性[5]。

假设盘式制动系统故障树的各底事件发生的模糊概率已知，则根据模糊数学理论中的扩张原理可得到 “制动力不足” 这一顶事件发生的模糊概率的隶属函数，如果Φ-1（ν）≠φ，则：

如果Φ-1（ν）=φ，则： Φ（A1，A2，A3，…，A9）（ν）=0。其中，Φ（A1，A2，A3，…，A9）（ν）为发生制动力不足事件的模糊概率的隶属函数，Φ（x）为故障树的结构函数，Ai（ui）为第i 个事件发生的模糊概率的隶属函数。其中A1，A2，A3，…，A9分别表示故障树中的九个底事件： 闸盘表面污染、闸瓦温度过高、闸瓦接触不良、油缸卡阻、闸瓦间隙超限、制动盘偏摆过大、碟形弹簧失效、残压过高和制动油过热。“∨” 和 “∧” 分别为取最大和取最小运算。

然后我们需要得出底事件的模糊概率的隶属函数。设论域U 为实数域R，记A（u）为u 对A 的隶属度，则A（u）亦为A 的隶属函数。模糊数的隶属函数可以有多种形式，最简单的是线性分布隶属函数。如图3 中线性函数所示，其代数运算较为容易。该隶属函数用公式表示为：

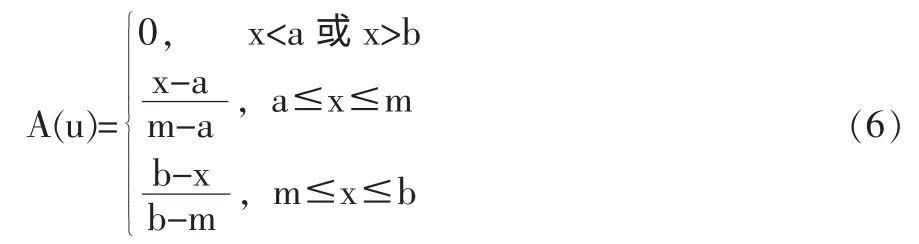
实际数据结合该公式即可求出模糊可靠度，进而求出顶事件的模糊概率，完成提升机盘式制动系统的可靠性分析。

图3 线性模糊数Fig.3 Linear fuzzy function

4 结束语

盘式制动系统是矿井提升机安全生产的基础，其可靠性直接关乎生命安全和生产效率。所以加强对提升机制动系统安全性研究是防止事故发生的重要举措，并且对盘式制动系统的维护保养一定要加以重视。

本文提出了盘式制动系统的模糊故障树，运用模糊数解决了对盘式制动系统进行可靠性分析时没有充足的采样样本来这一瓶颈。

[1] 李炳文，万丽蓉，等.矿山机械[M].徐州:中国矿业大学出版社，2010.

[2] 李生军.矿井提升机液压制动系统可靠性分析与探讨[J].中国矿山工程，2013，4.

[3] 程五一，等.系统可靠性理论[M].北京:中国建筑工业出版社，2010.

[4] 程居山，王昌田，等.矿山机械[M].徐州:中国矿业大学出版社，2005.

[5] 宋保维，毛昭勇，李正，等.系统可靠性设计与分析[M].西安：西北工业大学出版社，2008.