在建模活动过程中促进学生数学语言的转换

李海东

斯托利亚尔认为，“数学教学就是数学语言的教学”[2]，学生如果能熟练进行数学语言的转换，就能提高分析问题和解决问题的能力。教师如果能把数学建模和数学语言的转换有机融合，课堂教学就能事半功倍。数学语言包括符号语言、文字语言和图形语言三种。文字语言是“数学化”的自然语言，能准确表达数学对象及其相互关系、能充分揭示数学知识的本质；符号语言是思维的高度浓缩，能非常精炼和准确地表达数学知识的内涵；图形语言不但是学生形象思维的有效载体，而且是学生形象思维的结果，还是学生进行抽象思维的工具，能准确表达知识的数学特征。虽然它们的表现形式不同，但表示相同数学知识的本质属性一致，彼此之间可以相互转换。现以“平行四边形面积”教学为例，谈谈如何引导学生在建模活动过程中进行数学语言的转换。

一、 经历模型准备过程，把图形语言转换为文字语言

模型准备就是教师通过展示现实生活中的数学原型，创设情境，引导学生从情境中抽象出数学问题，促进学生进行数学思考，为学生建立数学模型做好准备工作。模型准备能激发学生的学习兴趣、唤醒学生的探究欲望。模型准备需要根据学生的最近发展区设计：可以由教师直接提出问题，也可以由教师通过讲故事的形式引导学生提出问题，还可以由教师出示图形引导学生提出问题。学生在模型准备过程中抽象数学问题时，往往需要进行语言转换：或者是文字语言之间的相互转换，或者是图形语言转换为文字语言。

课始，笔者用课件出示一个长方形花坛和一个平行四边形花坛图（图1）：

让学生比较哪个花坛大些？学生根据直觉无法判断，认为要根据它们的面积才能比较。笔者给花坛图标上数据后，学生很快用长×宽求出长方形的面积，但不会求平行四边形面积。于是，笔者先引导学生回忆平行四边形的特征和面积的意义，接着让学生表示图2中平行四边形的面积，最后引导学生说说图中3个数据分别表示的意义，认识平行四边形的底（6厘米）、高（4厘米）以及与底相邻的边（图中5厘米长的线段），帮助学生完成模型准备的过程。

在模型准备过程中，引导学生把图形语言转换成文字语言，不但能激发他们的探究兴趣，而且能为他们探究新知、建构数学模型奠定基础。

二、 经历模型验证过程，把文字语言转换为图形语言

模型验证就是学生根据已有认知发展水平和知识经验基础，结合自己的观察和思考提出猜想或假设，但假设可能是正确的，也可能是错误的，需要设计出一些有效的方法对学生提出的假设进行判断，为后续研究确定正确的方向。学生在验证过程中，需要有目的地进行操作、交流或质疑等活动。在这个过程中，学生不可避免地需要借助语言转换肯定或否定自己的假设。操作验证就是把假设的文字语言转换为图形语言。

学生根据长方形和正方形面积公式猜测图2中平行四边形的面积时，有的学生认为是5×6=30平方厘米，有的学生认为是5×4=20平方厘米，还有的学生认为是6×4=24平方厘米。这三种假设是否正确呢？学生经过思考，认为同一个平行四边形面积不可能有三种不同的结果。也就是说，可能有一种答案正确，也可能三种答案都不对。怎么验证呢？学生合作用边长1厘米的小正方形进行操作：

图3 图4

发现图3中铺上5×4=20个小正方形时，不能铺满整个平行四边形，也就是说平行四边形的面积比20平方厘米大，因此5×4=20平方厘米是错误的；继续铺小正方形，图4中铺上7×4=28个小正方形时，超出了平行四边形，也就是说平行四边形的面积小于28平方厘米，因此5×6=30平方厘米是错误的。剩下的假设——6×4=24平方厘米是否正确呢？笔者借助课件演示，把图5转化成图6，学生发现平行四边形的面积真的是6×4=24平方厘米。

图5 图6

用边长1厘米的小正方形验证假设是否正确，就是学生把文字语言转换成图形语言的过程，不但直观，而且具有很强的说服力，凸显了图形语言的优势。借助图形语言，学生不断验证猜想、否定猜想，并最终发现正确的猜想。学生在验证假设的过程中不断把文字语言转换为图形语言，同时初步感悟了数学模型。

三、 经历模型确立过程，把图形语言转换为符号语言

数学建模的目的不只是为了获得结论，更是为了促进学生在确立数学模型的过程中内化知识、升华思想。确立数学模型时，我们要引导学生根据自己的实践，结合所观察的现象，归纳、概括出模型内部因素之间的数量关系或具体算法（公式、法则或运算律等），以便确立相应的数学结构，建构数学模型。数量关系或具体算法往往要用字母表示，这就需要学生把图形语言转换成符号语言。

笔者先出示图7让学生判断两个图形的面积是否相等，并说说理由，学生思考后认为把左图中凸出的小三角形剪开、平移后就能拼成右边的长方形，因而面积相等；接着笔者出示一个平行四边形让学生尝试转化成长方形：有的学生沿平行四边形的高剪下一个三角形转化成长方形；有的学生沿平行四边形的高剪下一个梯形转化成长方形。然后，笔者引导学生思考为什么要沿着高剪开？一共有多少种剪法？为什么？转化后的长方形和原来的平行四边形有什么关系？转化后的长方形的长和宽与原来平行四边形的底和高之间分别有什么关系？根据长方形的面积公式猜一猜如何计算平行四边形的面积？学生独立思考后小组交流，很快发现平行四边形和转化后的长方形之间的关系，并根据“长方形的面积=长×宽”类推出“平行四边形的面积=底×高”。最后，笔者引导学生尝试用符号表示平行四边形的面积公式。学生尝试用个性化符号表示后，发现用字母表示最简洁，最终归纳出用“s=ah”表示平行四边形面积的方法。

学生建构平行四边形面积公式模型的过程，就是学生进行数学语言转换的过程：把平行四边形转化成长方形，实现了图形语言之间的转换；归纳概括出平行四边形的面积=底×高，实现了图形语言转换成文字语言；把文字语言表示的公式用字母表示，实现了文字语言转换成符号语言。在不断转换的过程中，学生经历了具体事物、个性化符号表示和“数学地表示”的逐步符号化过程，不但学会用简洁的符号语言表示平行四边形面积，而且初步掌握了数学建模方法。

四、 经历模型拓展过程，把图形语言转换为图形语言

根据具体问题构建数学模型不是学生认识的最终目的，我们还要有的放矢地引导学生把数学模型还原为具体的数学直观或可感的数学现实，拓展已有的数学模型。拓展数学模型就是引导学生对模型结构进行适当变化，促进学生把大脑中已有的认知结构进行重组和优化，产生新的数学模型。拓展数学模型，不但能帮助学生巩固已经建构的数学模型，而且能促使学生灵活应用数学模型，从而培养学生思维的灵活性。学生在拓展数学模型的过程中，同样离不开数学语言的转换。

模型拓展时，笔者引导学生解决下面两个问题：

1.在方格纸上画两个形状不同的平行四边形，使它们的面积都和图中长方形的面积相等。（图中方格边长都是1厘米）

2.先画一组平行线，再画一组平行线，可能画出什么图形？

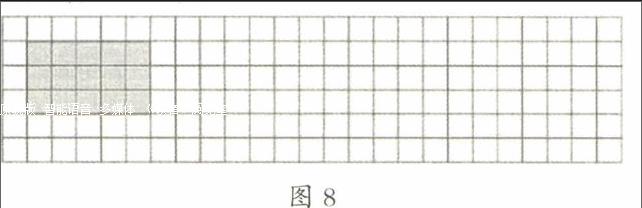
练习第1题时，学生尝试画图后，通过交流，发现画图时只要所画平行四边形的底和高与图中长方形的长和宽分别相等，那么所画图形和它的面积就相等，进而发现满足底×高=15平方厘米的平行四边形都符合要求；练习第2题时，有的学生画出了长方形、有的学生画出了正方形，有的学生画出了平行四边形。交流后，我出示图9，引导学生观察、分析这些等底等高的图形的面积相等。在此基础上，我出示图10，学生猜想后再用课件演示图形平移的过程（图11），验证学生的猜想——面积相等。

学生画平行四边形的过程就是长方形和平行四边形图形语言的转换；学生画2组平行线，是线与面图形语言之间的转换；学生判断不规则图形和平行四边形的面积是否相等，是不规则图形和规则图形之间的语言转换。这样借助图形语言之间的相互转换，学生不但丰富了知识表象，而且拓展了数学模型——等底等高的平行四边形面积相等，还进一步内化了数学模型，初步形成了模型思想，提高了学生学习数学的兴趣和应用意识。

总之，引导学生充分经历数学建模过程，不但有助于学生形成知识网络，而且能促进学生合理使用各种数学语言，帮助学生加深对数学知识、数学思想和数学方法的理解，还能提升学生分析问题和解决问题的能力，从而提高教学效率。当然，教学过程中的文字语言，图形语言和符号语言不是绝对孤立转换的，有时是几种语言的相互转换，有时还要借助自然语言和数学语言的转换才能达成教学目标。

【责任编辑：陈国庆】