横观各向同性水敏性地层斜井眼坍塌压力确定
2015-01-20刘明国晁文学
兰 凯,刘明国,晁文学
中石化中原石油工程有限公司钻井工程技术研究院,河南 濮阳 457001
横观各向同性水敏性地层斜井眼坍塌压力确定
兰 凯,刘明国,晁文学
中石化中原石油工程有限公司钻井工程技术研究院,河南 濮阳 457001
在以泥页岩为目标储层的非常规油气藏水平井开发中,钻遇井壁的稳定性问题突出,一方面是由于在设计钻井液密度时简单采用各向同性介质模型和Mohr-Coulomb强度准则,另一方面则是由于选用的钻井液性能欠佳,难以保证建井全过程的井壁稳定。为此,将地层视为横观各向同性介质,采用Mogi-Coulomb强度准则判别岩石基体和层理面的稳定性,同时考虑泥页岩水化作用对岩石力学强度参数的影响,建立了水敏性地层井壁稳定分析模型,分析了坍塌压力随井斜、方位、钻井液性能、钻井时间等因素的变化规律。研究结果表明:对于具有显著层理面结构的泥页岩地层,采用横观各向同性模型比各向同性介质模型更能描述强度的各向异性;采用Mogi-Coulomb准则比Mohr-Coulomb强度准则得到的坍塌压力值与实际吻合程度更高,在保证井壁稳定的前提下有利于降低钻井液密度,实现钻井提速;提高钻井液封堵能力、减小泥页岩吸水扩散能力,有利于延长坍塌周期。利用东濮、威远、焦石坝等工区多口页岩气水平井的实钻资料对本文方法进行了验证,证实本文方法确定的钻井液密度窗口下值更能满足安全钻井需求。
横观各向同性;泥页岩;斜井眼;坍塌压力;井壁稳定;钻井
0 引言
水敏性地层井壁稳定一直都是钻井工程领域的重要课题,主要包括井壁坍塌和破裂两种基本类型,其研究有助于确定合理的钻井液密度窗口和井身结构设计。其中井壁坍塌可归结为井壁岩石所受的应力超过其本身的强度从而产生剪切破坏,若不能准确预知地层坍塌压力,则无法设计合理的钻井液密度下限值。在非常规油气资源的长水平段水平井开发中,经常会钻遇大段水敏性泥页岩,不恰当的钻井液下限密度设计易引起井壁垮塌、缩径或漏失,从而影响后期固井质量和压裂效果,制约开发效率。
从井壁稳定的岩石力学机理出发预测坍塌压力时,最典型的做法是假定岩石为线弹性、均质的各向同性材料[1],采用Mohr-Coulomb强度准则[2]或Drucker-Prager强度准则[3-4]判断井壁坍塌条件。Ewy等[5]研究表明,泥页岩有着显著的各向异性强度;而Ong等[6]对斜井眼井壁剪切破坏的参数敏感性研究则表明岩石的各向异性对井壁稳定具有重要影响;Zhang等[7]对井壁稳定分析中选用的各种岩石力学强度准则给出了详细的研究,指出三维Hoek-Brown[8]和Mogi-Coulomb准则更适用。
对于各向异性地层,Aadnoy等[9]、Ong[10]、Gupta等[11]、崔杰等[12]、李军等[13]建立了井周应力分布公式,金衍等[14]、卢运虎等[15]、闫传梁等[16]、谭强等[17]应用弱面破坏准则分析了各向异性地层井壁稳定问题。但这种单一弱面准则实质上依然是考虑弱面的Mohr-Coulomb准则,其计算的坍塌压力结果偏保守。
鉴于此,为保证水敏性泥页岩地层的安全钻井,笔者在前人研究基础上,提出了基于线弹性横观各向同性假设、Mogi-Coulomb强度准则、考虑泥页岩水化效应的斜井眼坍塌压力计算方法。
1 横观各向同性地层中斜井眼井周应力
1.1 井周应力基本方程
假设地层为横观各向同性、线弹性、均匀连续介质,Dinesh Gupta等[11]在前人研究基础上推导了斜井眼井壁上的应力分布解析表达式:
其中:
D′=(pw-σx,o)cosθ-τxy,osinθ-i[(pw-σx,o)sinθ+τxy,ocosθ] ;
E′=-(pw-σy,o)sinθ+τxy,ocosθ-i[(pw-σy,o)cosθ+τxy,osinθ] ;
F′=-τxz,ocosθ-τxz,osinθ-i[τxz,ocosθ-τxz,osinθ] 。
式中:σx、σy、σz、τxy、τxz和τyz为井壁围岩的应力分量;σx,o、σy,o、σz,o、τxy,o、τxz,o和τyz,o为原地应力场引起的井周应力;μk(k=1, 2, 3)是与应变协调方程对应的特征方程的特征根,其值由柔度矩阵系数确定;λk(k=1, 2, 3)是与特征根有关的系数;a31,a32,…,a36为应变柔度矩阵系数;zk(k=1, 2, 3)是与井壁围岩坐标相关的复变量,zk=x+μky,x和y分别为井壁围岩计算点的坐标;Re为复数的实部;pw为钻井液柱压力;θ为井眼坐标系中计算点与x方向夹角,即井周角。
1.2 原地应力场的坐标转换
在各向异性地层的井壁稳定性分析中,通常用到多套坐标系(图1),即地应力主坐标系xsyszs、井眼直角坐标系xbybzb。
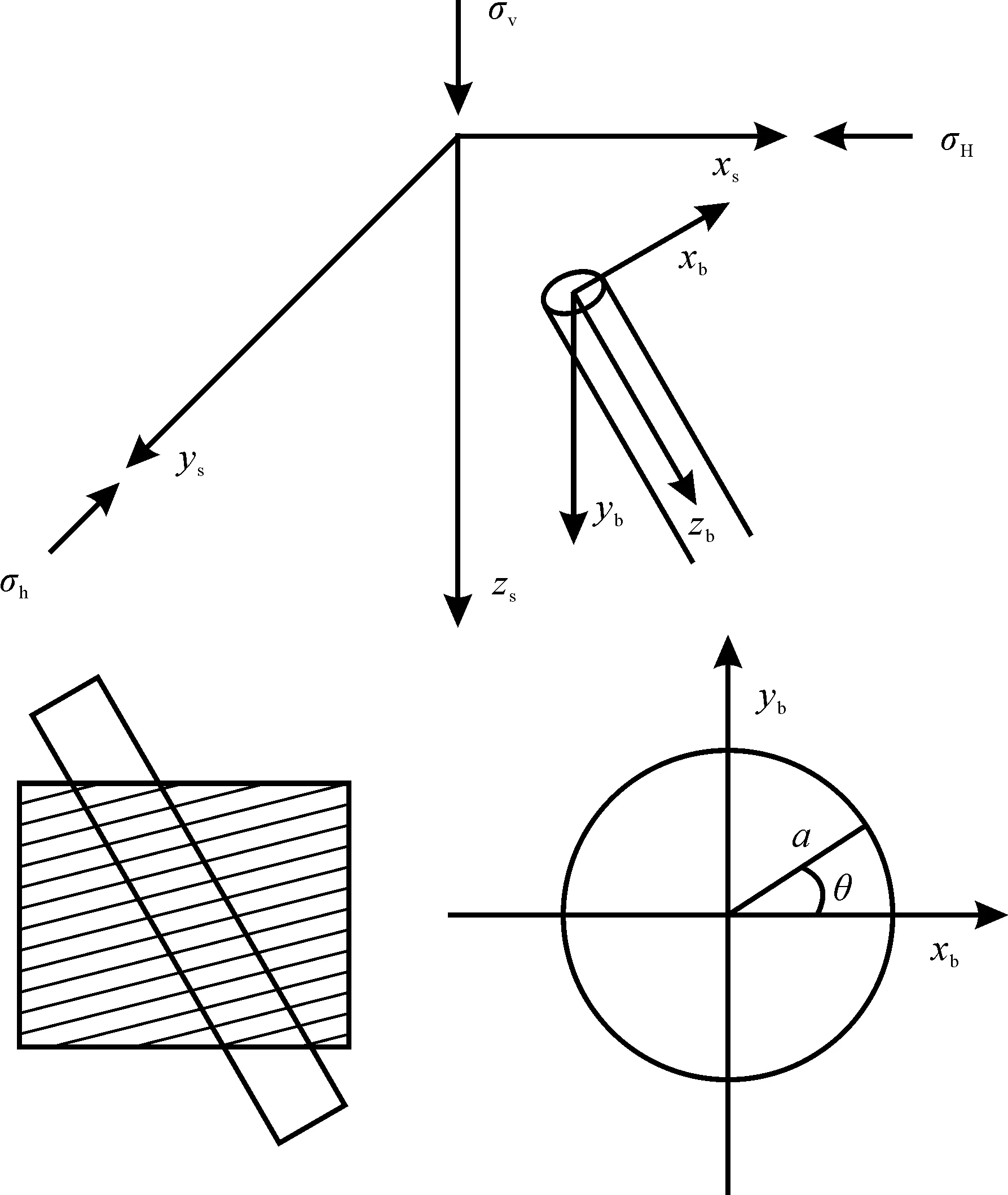
σh.最小水平主应力;σH.最大水平主应力;σv.垂向地应力;a.井眼半径;θ.井周角。图1 泥页岩地层井周应力分布和坐标体系示意图Fig.1 Coordinate system and stress distribution around borehole wall in mudstone/shale strata
设井斜角为α、方位角为β,则从地应力坐标系到井眼直角坐标系的转换关系为
因此在井眼直角坐标系中,原地应力场作用下井壁上的应力分量可以表达为
将式(2)代入式(3),可进一步得到应力分量表达式:
1.3 井周应力的极坐标表达式
从井眼直角坐标系到极坐标系的转换关系为
根据平面应变弹性力学理论,极坐标系下的井周应力表达式为

1.4 泥页岩水化强度折减效应
钻进泥页岩井段时,不管是水基钻井液体系还是油基钻井液体系,泥页岩层段总存在不同程度的水化膨胀,不仅改变井周围岩应力分布,也改变了岩石的材料力学参数。金衍等[18]根据中国石油大学岩石力学实验室的室内测定,得到了水化膨胀后泥页岩的黏聚力c、内摩擦角φ、弹性模量E、泊松比ν与地层含水量w的关系:
式中:w(r, t)为距离井眼中心r处t时刻吸附水的质量分数;wa为井壁上的含水量;w∞为地层原始含水量;c0为水化前黏聚力;φ0为水化前内摩擦角;ν0为水化前泊松比;E1为水化前弹性模量;E2为实验数据回归的与弹性模量相关的变量。
2 井壁坍塌破坏强度准则
水敏性泥页岩的剪切破坏遵从Mogi-Coulomb准则[19],可用主应力表示为

3 井周应力分布及坍塌压力变化规律
考虑井斜角、原地应力状态及泥页岩水化等共同作用,编制出计算井壁围岩应力分布状态和坍塌压力变化规律的计算程序,计算用参数见表1[16]。
3.1 各向异性对井周应力分布的影响
图2为40MPa钻井液柱压力下沿最小水平主应力方向延伸的井眼,在考虑介质的各向异性和不考虑各向异性时井壁上的切向应力对比。从图2可以看出:视地层为各向异性介质时计算出的井周应力要远大于视为各向同性介质,且随着井斜角的增加差值越来越大。这说明,采用各向同性介质模型不能充分反映带有显著沉积特性的各向异性泥页岩地层井壁围岩受力状态,由此求得的钻井液安全密度窗口过宽(图3),难以有效指导现场施工。
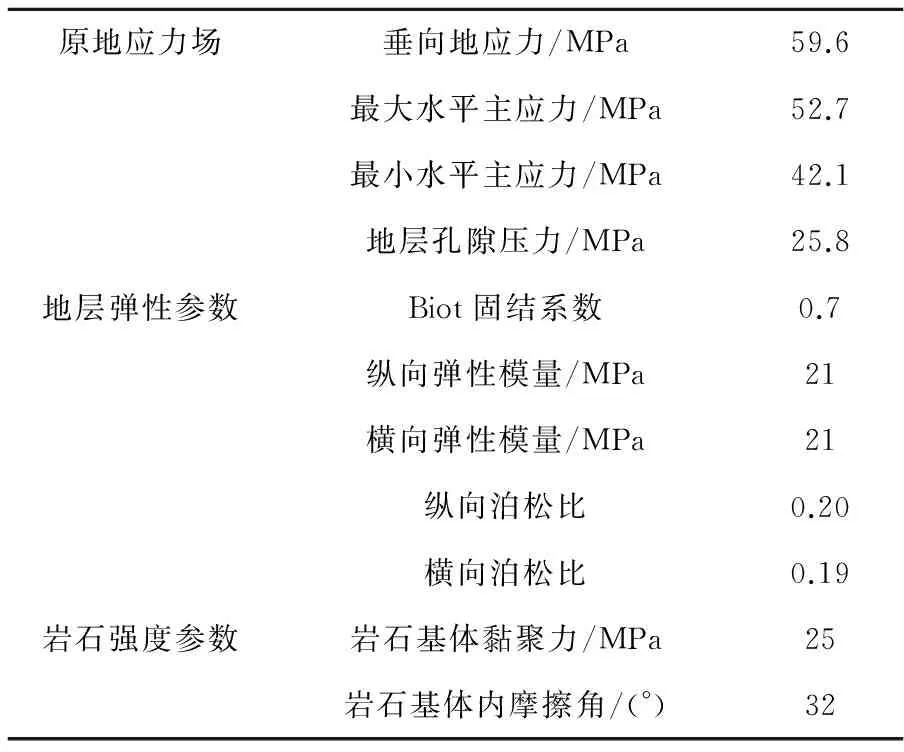
表1 模拟用储层计算参数
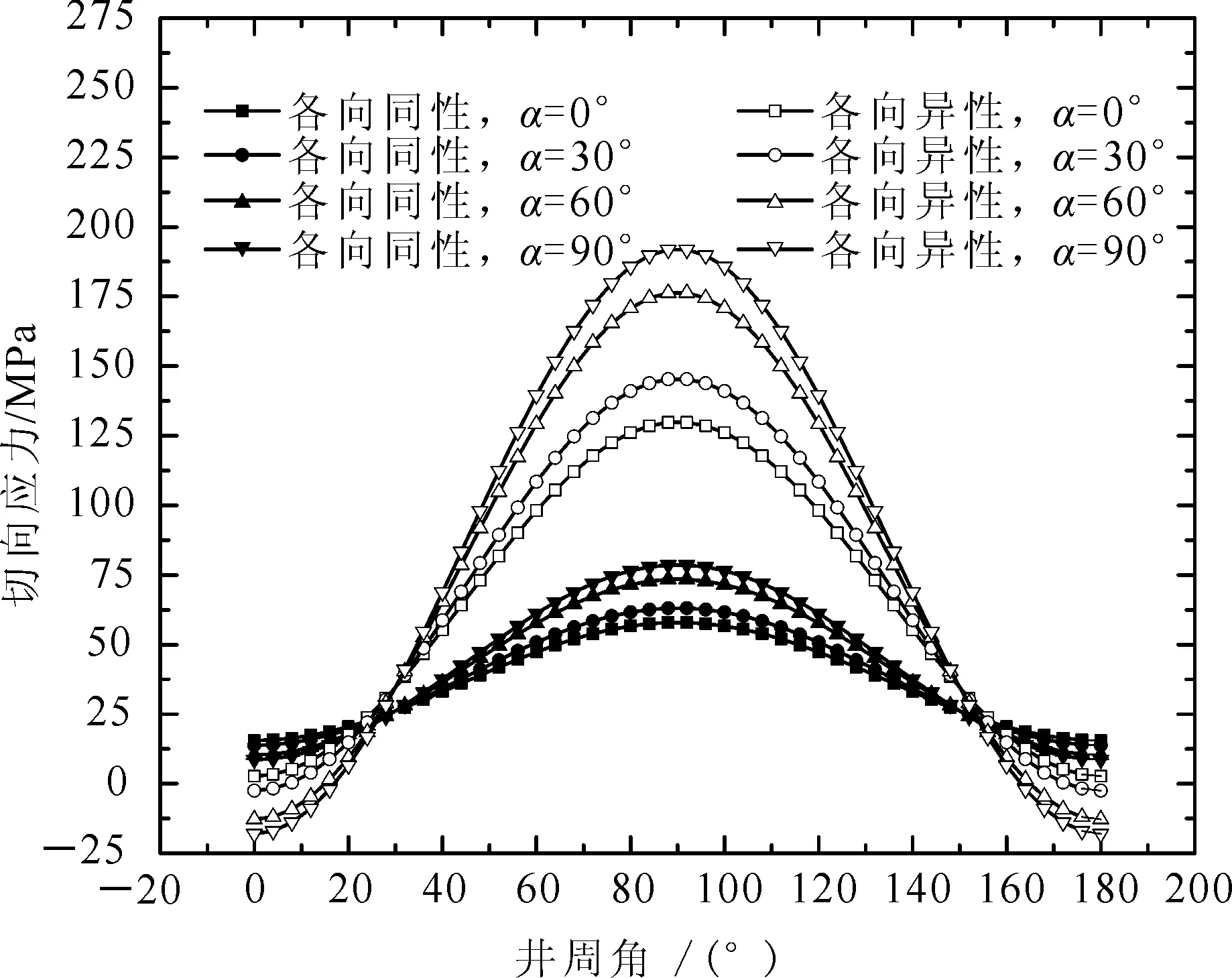
图2 pw=40 MPa、β=90°时各向同性和各向异性模型井周切向应力对比Fig. 2 Tangential stress comparison between isotropic and anisotropic using model when pw=40 MPa and β=90°

图3 各向同性和横观各向同性模型计算坍塌压力对比Fig.3 Comparison of calculated collapse pressure isotropic and transversely isotropic models
3.2 强度准则对坍塌压力的影响
Mohr-Coulomb准则因其忽略中间主应力对岩石强度的影响,所计算出的坍塌压力值过高、安全密度窗口偏保守,这点已为前人的研究证实;而在实践中,过高的钻井液密度亦会引起钻井过程中的井漏、钻柱黏卡、泵压高等问题。图4为基于横观各向同性介质模型,分别采用Mohr-Coulomb(M-C)准则和Mogi-Coulomb(MG-C)准则所计算出的坍塌压力。从图4对比可以看出:Mogi-Coulomb强度准则考虑了中间主应力的影响,计算出的坍塌压力值小于Mohr-Coulomb准则的结果,但显著高于采用常规各向同性均匀介质假设的结果(图3),可信度更高。

图4 横观各向同性模型采用不同强度准则的预测坍塌压力对比Fig.4 Comparison of calculated collapse pressure using different strength criteria and transversely isotropic model
图5为采用横观各向同性介质模型和Mogi-Coulomb强度准则计算出的沿不同井斜、方位延伸井眼的坍塌压力图版。从图5可以看出:在模拟计算采用的正断层地应力模式下,沿最小水平主应力方向为最安全钻井方向;在小井斜角情况下,坍塌压力随方向变化不大,但在大井斜角情况下变化显著;在最安全钻井方向存在一个安全的井斜角区间,即30°~50°。
3.3 钻井液性能对井壁稳定周期的影响
对于强水敏性的泥页岩地层,为保障井眼作业期间的长效稳定,通常采用油基钻井液体系,但是这也面临成本、环保等方面的巨大压力;因此研发低成本高性能钻井液体系、配合钻井液安全密度窗口合理控制从而实现井壁稳定的需求迫切。图6为沿最小水平主应力方向延伸的井眼,采用泥页岩吸水扩散系数Cf分别为0.013 4和0.024 3 cm2/h的2种钻井液体系时,坍塌压力随井斜角和水化时间变化情况。从图6可以看出:吸水扩散系数越大,水化作用越强烈,坍塌压力越大,即减小泥页岩吸水扩散系数有利于降低水化影响、提高井壁稳定性。总之,坍塌压力随着井斜角增大而增大,在计算水化时间内随着时间的增加而增大,但在井斜角30°~50°区间内坍塌压力有波动。
为进一步明确在钻井液浸润环境下,泥页岩地层坍塌压力随水化作用影响的变化规律,图7给出了基于横观各向同性介质模型和Mogi-Coulomb强度准则、吸水扩散系数为0.013 4 cm2/h、方位角为90°时,坍塌压力随井斜和水化时间变化趋势。从图7可以看出,坍塌压力与水化作用时间关系复杂:对于大斜度井眼,井壁坍塌周期为10 d左右; 当井下作业时间较长时,井斜角50°左右为井壁稳定最薄弱处。总之,在泥页岩水化作用下,井斜角增大,井壁坍塌周期缩短,即大斜度井段井壁稳定需求更大。
3.4 层理弱面对坍塌压力的影响
为分析层理面方向对地层坍塌压力的影响,假定地层的层理面倾角为15°、倾向为0°,计算得到坍塌压力的变化规律如图8所示。对比图5和图8,可以看出:层理弱面的存在使得井壁岩石更可能出现沿弱面的剪切破坏而不是岩石基体的破坏[20],因此其坍塌压力要高于不考虑层理面时的坍塌压力;当井斜角大于45°、井眼轨迹与最大水平主应力夹角小于55°时,层理弱面对坍塌压力的影响显著,这表明当井眼轨迹与层理面的入射夹角较小时地层稳定性差;当井眼轨迹与最小水平主应力方向一致时,在井斜60°以内层理面的存在对坍塌压力无明显影响,因此,最小水平主应力方向为最安全的钻井方位。

图5 不同井斜和方位条件下坍塌压力变化规律Fig.5 Collapse pressure variation with well deviation angle and azimuth angle
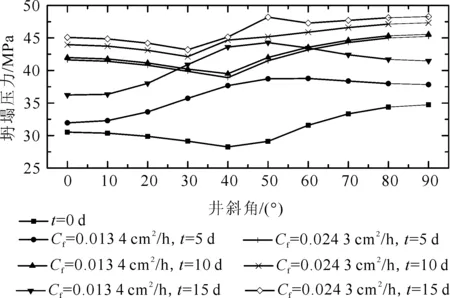
图6 β=90°时不同钻井液体系下坍塌压力随井斜和时间的变化曲线Fig.6 Collapse pressure variation with well deviation angle and time using different drilling fluid systems when β=90°
4 现场应用
4.1 东濮凹陷沙河街组泥页岩水平井验证
W88-1HF井目标储层为沙3中的页岩夹致密薄砂岩,埋深3 569.6 m;设计时没有考虑泥页岩水化对井壁稳定的影响,采用三开井身结构;设计二开Φ244.5 mm技术套管封至50.00°井斜处,实际下至3 330 m(49.62°)。三开实钻采用水基钻井液体系,在钻至3 589 m后短起下,于3 500 m(井斜71.10°)处第一次遇卡,循环返出大量黑色泥岩掉块;进行钻进液防塌性能处理后继续钻进至3 853 m起钻换钻头和螺杆,起钻多点遇卡;于3 390 m(井斜69.00°)上提摩阻300 kN。这与本文分析得到的50~70°内井壁稳定性差的结果相吻合(图7)。
而具有同样储层类型的W68-2HF井改用四开井身结构,三开技术套管封至A靶点(井斜85.27°),四开采用油基钻井液体系,1 302 m水平段平均井径扩大率仅为3.89%,既规避了大斜度井段的井壁稳定性风险,又保证了水平段泥页岩井壁稳定。
4.2 威远龙马溪组页岩气水平井验证
威远地区威201井区龙马溪组页岩气藏属走滑断层地应力机制,层理面倾角为10°,图9为采用不同模型和强度准则时坍塌压力计算结果对比。采用各向同性介质模型且不考虑层理面影响时,地层坍塌压力当量密度约为1.05 g/cm3。威201-H1井设计方位沿最小水平井主应力方向,A点垂向深度1 526 m,B点垂向深度1 570 m,采用本文中的横观各向同性介质模型和Mogi-Coulomb强度准则,计算得到水平段坍塌压力当量密度约为1.60 g/cm3;考虑层理弱面影响和泥页岩水化效应后,坍塌压力当量密度逐步提高到1.80 g/cm3以上。
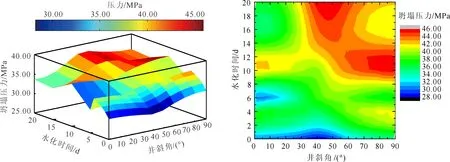
图7 β=90°、Cf=0.013 4 cm2/h时坍塌压力随井斜和时间的变化趋势Fig. 7 Collapse pressure variation with well deviation angle and time when β=90° and Cf=0.013 4 cm2/h
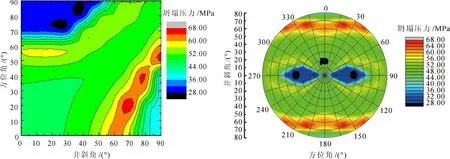
图8 考虑层理面影响时,不同井斜和方位条件下坍塌压力变化规律Fig. 8 Collapse pressure variation with well deviation angle and azimuth angle taking bedding plane into consideration
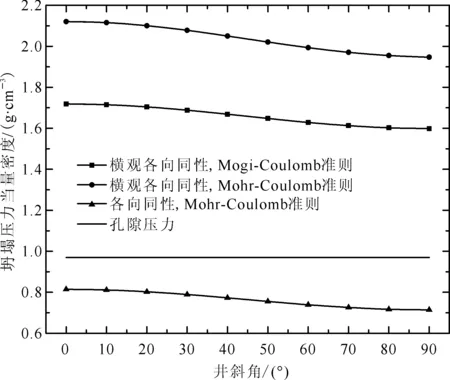
图9 威201井区采用不同模型和强度准则对比沿最小水平地应力方向坍塌压力变化规律Fig.9 Collapse pressure variation when drilling along minimum horizontal stress in Wei201 district, using different models and strength criteria
在实钻中采用密度1.20~1.22 g/cm3的钻井液时井筒垮塌严重、层理性掉块多;将密度提高至1.62 g/cm3后仍存在井下复杂情况;之后采用1.80 g/cm3以上的钻井液后逐步恢复正常[21]。邻近的威201-H3井从侧钻段到水平段采用油基钻井液密度为1.70~1.83 g/cm3(最高达1.85 g/cm3)时井眼稳定[22]。
4.3 焦石坝龙马溪组页岩气水平井应用
涪陵焦石坝区块位于川东高陡褶皱带包鸾——焦石坝背斜带焦石坝构造,目的层为龙马溪组底部页岩气层,埋深约2 400 m,压力系数1.41~1.45,水平井段方位垂直于最大水平主应力方向或与最大水平主应力方向斜交(不超过30°)[23]。采用本文中的横观各向同性介质模型和Mogi-Coulomb 强度准则,考虑层理弱面的影响时计算得到:二开井段龙马溪组坍塌压力当量密度为1.08~1.17 g/cm3,采用水基钻井液体系泥页岩水化15 d后坍塌压力逐步提高到1.43 g/cm3以上;三开井段龙马溪组坍塌压力当量密度为1.55~1.72 g/cm3。
在焦页1-3HF井龙马溪组实钻中,二开水基钻井液密度1.30~1.32 g/cm3、平均井眼扩大率4.21%,三开油基钻井液密度1.50~1.65 g/cm3(最高1.68 g/cm3)、平均扩大率-1.29%、钻井周期17.82 d,全井未出现井壁坍塌问题。焦页1HF是在焦页1井基础上侧钻而成,二开龙马溪组实钻水基钻井液密度为1.44 g/cm3,从钻开地层到中完电测地层受钻井液浸泡时间达96 d,因此井壁在中完期间发生井壁严重垮塌,平均井眼扩大率达17.95%;三开油基钻井液密度1.45~1.55 g/cm3(最高1.65 g/cm3)、平均扩大率1.05%、钻井周期16.10 d,未出现井壁坍塌问题。
5 结论与建议
1)对于具有显著层理面结构的泥页岩地层,采用各向同性介质模型得到的井壁岩石应力极值偏小,其计算得到的坍塌压力值过低,难以有效描述地层强度和地应力的各向异性,建议采用横观各向同性模型。
2)Mohr-Coulomb强度准则忽略中间主应力的影响所得到的坍塌压力值过于保守,而采用Mogi-Coulomb准则得到的坍塌压力值与实际吻合程度高,在保证井壁稳定的前提下有利于降低钻井液密度,减小井底压持效应、实现钻井提速、降低钻井成本。
3)对于以泥页岩为目的层的非常规油气藏水平井,钻井液性能对维持井壁稳定至关重要。提高钻井速度,在泥页岩坍塌周期内完成建井作业有利于规避风险;同时,提高钻井液封堵能力、减小泥页岩吸水扩散能力,有利于延长坍塌周期。
4)显著层理弱面的存在使得井壁稳定问题更为突出,合理设计井眼方位和穿过层理面的井斜角度有利于缓解层理弱面的影响。
[1] Bradely W B. Failure of Inclined Boreholes[J]. Journal of Energy Resources Technology, 1979, 101(4): 232-239.
[2] Lee H, Ong S H, Azeemuddin M, et al. A Wellbore Stability Model for Formations with Anisotropic Rock Strengths[J]. Journal Petroleum Science and Engineering, 2012, 96/97: 109-119.
[3] 张公社, 李永康, 尹俊禄, 等. 沁水盆地煤层气井坍塌压力预测[J].石油钻采工艺, 2010, 32(4): 96-98. Zhang Gongshe, Li Yongkang, Yin Junlu, et al. Prediction of Collapse Pressure for CBM Wells in Qinshui CBM Fields[J]. Oil Drilling & Production Technology, 2010, 32(4): 96-98.
[4] 兰凯, 熊友明, 闫光庆, 等. 川东北水平井储层井壁稳定性及其对完井方式的影响[J]. 吉林大学学报:地球科学版, 2011, 41(4): 1233-1238. Lan Kai, Xiong Youming, Yan Guangqing, et al. Horizontal Borehole Stability and Its Influence on Well Completion Optimization in the Northeast Sichuan Basin[J]. Journal of Jilin University: Earth Sciences Edition, 2011, 41(4): 1233-1238.
[5] Ewy R T, Govber C A, Stankovic R J. Strength Anisotropy of Mudstones and Shales[C]//44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium. Salt Lake City: Utah, 2010.
[6] Ong S H, Roegiers J C. Influence of Anisotropies in Borehole Stability[J]. International Journal of Rock Mechanics and Mining Sciences, 1993, 30(7): 1069-1075.
[7] Zhang L, Cao P, Radha K C. Evaluation of Rock Strength Criteria for Wellbore Stability Analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(8): 1304-1316.
[8] 周念清, 杨楠, 汤亚琦, 等. 基于Hoek-Brown准则确定核电工程场地岩体力学参数[J]. 吉林大学学报:地球科学版, 2013, 43(5): 1517-1522, 1532. Zhou Nianqing, Yang Nan, Tang Yaqi, et al. Determination of Rockmass Mechanical Parameters of Nuclear Power Engineering Site Based on Hoek-Brown Criterion[J]. Journal of Jilin University: Earth Sciences Edition, 2013, 43(5): 1517-1522, 1532.
[9] Aadnoy B S, Chenevert M E. Stability of Highly Inclined Boreholes[J]. SPE Drilling Engineering, 1987, 2(4): 364-374.
[10] Ong S H. Borehole Stability[D]. Oklahoma: University of Oklahoma, 1997.
[11] Gupta D, Zaman M. Stability of Boreholes in a Geological Medium Including the Effects of Anisotropy[J]. Applied Mathematics and Mechanics, 1999, 20(8): 837-866.
[12] 崔杰, 焦永树, 曹维勇, 等. 各向异性地层中井孔周围应力场的研究[J]. 工程力学, 2011, 28(7): 31-36. Cui Jie, Jiao Yongshu, Cao Weiyong, et al. A Study on the Stress Field Around a Borehole in Anisotropic Formation[J]. Engineering Mechanics, 2011, 28(7): 31-36.
[13] 李军, 柳贡慧, 陈勉. 正交各向异性地层井壁围岩应力新模型[J]. 岩石力学与工程学报, 2011, 30(12): 2481-2485. Li Jun, Liu Gonghui, Chen Mian. New Model for Stress of Borehole Surrounding Rock in Orthotropic Formation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2481-2485.
[14] Jin Y, Yuan J, Hou B, et al. Analysis of the Vertical Borehole Stability in Anisotropic Rock Formations[J]. Journal of Petroleum Exploration and Production Technology, 2012, 2(4): 197-207.
[15] 卢运虎, 陈勉, 袁建波, 等. 各向异性地层中斜井井壁失稳机理[J]. 石油学报, 2013, 34(3): 563-568. Lu Yunhu, Chen Mian, Yuan Jianbo, et al. Borehole Instability Mechanism of a Deviated Well in Anisotropic Formations[J]. Acta Petrolei Sinica, 2013, 34(3): 563-568.
[16] 闫传梁, 邓金根, 蔚宝华, 等. 页岩气储层井壁坍塌压力研究[J]. 岩石力学与工程学报, 2013, 32(8): 1595-1602. Yan Chuanliang, Deng Jingen, Wei Baohua, et al. Research on Collapsing Pressure of Gas Shale [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(8): 1595-1602.
[17] 谭强, 邓金根, 张勇, 等. 各向异性地层定向井井壁坍塌压力计算方法[J]. 断块油气田, 2010, 17(5): 608-610. Tan Qiang, Deng Jingen, Zhang Yong, et al. Calculation Method of Directional Borehole Collapse Pressure in Anisotropic Formations[J]. Fault-Block Oil & Gas Field, 2010, 17(5): 608-610.
[18] 金衍, 陈勉. 水敏性泥页岩地层临界坍塌时间的确定方法[J]. 石油钻探技术, 2004, 32(2): 12-14. Jin Yan, Chen Mian. A Method for Determining the Critical Time of Wellbore Instability at Water-Sensitive Shale Formations[J]. Petroleum Drilling Techniques, 2004, 32(2): 12-14.
[19] Al-Ajmi A M, Zimmerman R W. Relation Between the Mogi and the Coulomb Failure Criteria[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 431-439.
[20] Zhang Jincai. Borehole Stability Analysis Accounting for Anisotropies in Drilling to Weak Bedding Planes[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60: 160-170.
[21] 王华平, 张铎, 张德军, 等. 威远构造页岩气钻井技术探讨[J]. 钻采工艺, 2012, 35(2):9-11. Wang Huaping, Zhang Duo, Zhang Dejun, et al. Drilling Technologies on Shale Gas in Weiyuan Structure[J]. Drilling & Production Technology, 2012, 35(2): 9-11.
[22] 何涛, 李茂森, 杨兰平, 等. 油基钻井液在威远地区页岩气水平井中的应用[J]. 钻井液与完井液, 2012, 29(3): 1-5. He Tao, Li Maosen, Yang Lanping, et al. Application of Oil-Based Drilling Fluid in Shale Gas Horizontal Well in District of Weiyuan[J]. Drilling Fluid & Completion Fluid, 2012, 29(3): 1-5.
[23] 周贤海. 涪陵焦石坝区块页岩气水平井钻井完井技术[J]. 石油钻探技术, 2013, 41(5): 26-30. Zhou Xianhai. Drilling & Completion Techniques Used in Shale Gas Horizontal Wells in Jiaoshiba Block of Fuling Area[J]. Petroleum Drilling Techniques, 2013, 41(5): 26-30.
Determination of Collapse Pressure for Deviated Wellbore in Transversely Isotropic Water-Sensitive Formation
Lan Kai, Liu Mingguo, Chao Wenxue
DrillingEngineeringTechnologyInstitute,ZhongyuanOilfieldServiceCorporation,Sinopec,Puyang457001,Henan,China
Borehole stability in shale/mudstone strata is significant during the construction of horizontal well for unconventional hydrocarbon reservoirs, which is caused by two mainly reasons, one is the current borehole stability design model using simply isotropic media model and Mohr-Coulomb criterion, and the other is the inappropriate performance of drilling fluid. To solve this problem, a new borehole stability model for water-sensitive formation was established, which adopted transversely isotropic media model, Mogi-Coulomb criterion, and the effect of hydration to rock strength. The influence of deviation angle, azimuth, drilling fluid performance and drilling time on collapse pressure were analyzed. The results showed that transversely isotropic model was more suitable to describe strength anisotropy for laminated shale/mudstone; collapse pressure calculated by Mogi-Coulomb criterion is more consistent with drilling practice than Mohr-Coulomb, in this case, lower drilling fluid density can be used to keep borehole stability and promote rate of penetration; enhance sealing capacity and decline shale hydration diffusion capacity were helpful to extend collapse cycle. Several examples of shale gas horizontal wells drilled in Dongpu, Weiyuan and Jiaoshiba districts confirmed that the recommended method is highly reliable and effective.
transversely isotropy; mudstone/shale; deviated borehole; collapse pressure; borehole stability; drilling
10.13278/j.cnki.jjuese.201501201.
2014-03-19
国家科技重大专项(2011ZX05017-002);中国石化科研项目(JP12005)
兰凯(1982——),男,高级工程师,博士,主要从事复杂结构井钻完井技术研究,E-mail:lank.oszy@sinopec.com。
10.13278/j.cnki.jjuese.201501201
TE21;TE28
A
兰凯,刘明国,晁文学. 横观各向同性水敏性地层斜井眼坍塌压力确定.吉林大学学报:地球科学版,2015,45(1):198-206.
Lan Kai, Liu Mingguo, Chao Wenxue. Determination of Collapse Pressure for Deviated Wellbore in Transversely Isotropic Water-Sensitive Formation.Journal of Jilin University:Earth Science Edition,2015,45(1):198-206.doi:10.13278/j.cnki.jjuese.201501201.
