基于两种神经网络模型的胶合板期货价格短期预测

刘大鹏 (北京林业大学经济管理学院，北京 100083)

基于两种神经网络模型的胶合板期货价格短期预测

刘大鹏 (北京林业大学经济管理学院，北京 100083)

选取2013年12月06日～2014年09月17日的胶合板主力期货合约作为训练样本，2014年09月18日～2014年11月05日的胶合板主力期货合约作为测试数据，采用L-M优化算法和贝叶斯优化算法的BP神经网络模型对期货价格进行了预测分析。结果表明，采用两种优化算法的神经网络模型均具有较高的拟合度，对价格走势有良好的预测效果，可为期货市场投资者投资决策提供一定的参考。

胶合板期货；价格预测；神经网络模型

期货交易是指交易双方在期货交易所买卖期货合约的交易行为，是商品现货交易的派生交易方式。利用期货交易,期货交易者能够更好地规避商品活动中的库存风险以及因资信、价格波动所带来的风险,从而实现商品的套期保值。期货价格亦被称作商品供求的“晴雨表”，它能够反映商品未来的供求关系。期货市场主要具有套期保值和价格发现的功能，但这都依赖于对期货价格走势的分析判断。

目前针对期货行情预测的研究已有不少研究成果，分别针对量、价、指数、资金管理、风险预警、指标体系以及其他资本市场互动等方面展开。例如基本分析法，即分析供给和需求等方面确定期货价格的走势；影响因素分析法，即分析影响供给和需求的相关因素如宏观经济政策、经济周期、利率水平、自然条件、政治因素和心理因素等确定一段时间内期货价格的走势；技术分析法，例如K线分析图、指标分析法、切线分析法等[1]，通过分析以往期货价格等指标预测未来价格的走势。但综合起来主要有以下几个特点：①多为定性分析，缺乏定量研究，且预测结果缺乏实践检验标准；②部分定量预测分析中采用BP神经网络，但其往往停留在一种算法层面，不利于发现针对期货行情预测的更优化的解决方法。

笔者选用采用L-M神经网络模型以及贝叶斯优化算法的BP神经网络模型两种方法对胶合板期货价格进行短期预测，对两种预测方法的预测结果进行对比，为投资者投资决策提供参考。

1 数据来源与研究方法

1.1 数据来源改革开放以来，我国陆续推出了多种期货合约，期货市场得到长足发展。大连商品交易所于1993年2月28日成立，于2013年12月6日起胶合板期货上市交易,并推出了多种胶合板期货合约。

该研究选取大连商品交易所2013年12月6日上市的胶合板期货合约作为研究对象。

根据大连商品交易所数据，大连商品交易所规定的胶合板期货合约尺寸如下：宽度为1 220，长度为2 440 mm，厚度分为2种，标准品厚度为15 mm，替代品厚度为18 mm，标准品和替代品的升贴水分别为0和15元/张。

胶合板期货价格受多种因素影响，包括宏观经济因素、相关产品价格、胶合板现货价格、往日胶合板期货价格等多种因素影响。

BP神经网络用于预测研究时可以采用回归分析和时间序列2种方式。由于该研究选取交易所日度价格作为输入变量，并以日度价格预测作为模型的输出变量。因此，若采用回归分析的预测方式，就要求模型的输入变量也必须为日度数据形式或相近维度的数据。但是，影响胶合板期货价格的因素种类繁多，宏观方面包括季节因素、气候因素等自然因素，经济形势、经济周期等经济因素，但宏观因素往往时间跨度较长，中短期内鲜有波动，因此该研究所作短期预测可忽略宏观因素的影响。笔者曾尝试将月度宏观数据带入神经网络模型中作为训练样本，但实践表明预测结果较差，甚至无法产生有效的结果。微观方面主要包括胶合板现货价格、相关上下游产品价格以及胶合板期货合约自身价格等因素，在微观层面的因素中由于现货价格地区差异性较大，现货价格统计滞后以致难以统计[2]。因此，在综合考虑以上因素后，为了尽可能地提高预测的准确性，经过多次尝试后，笔者选定了以下6个变量作为输入变量：当日开盘价、最高价、最低价、收盘价、当日成交量以及当日持仓量。

由于胶合板期货的时间跨度有限，任一交割月份的期货合约在合约到期后都将终止交易，且在同一交易日可能有若干个不同的合约在进行交易，为克服期货价格的不连续的特性，必然要求产生一个连续的价格和成交量时间序。因此该研究选取来源于Wind资讯的2013年12月6日～2014年11月5日连续的大连商品交易所胶合板期货合约数据构建BP神经网络模型。

1.2 研究方法该研究采用L-M神经网络模型以及贝叶斯优化算法的BP神经网络模型对上述数据进行回归分析并进行预测。

1.2.1BP神经网络模型。BP(Back-Propagation)神经网络是1986年由Rumelhart和McCelland率先提出的一种按误差逆传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络模型之一，其优点在于可以以任意精度逼近任何非线性函数。

BP神经网络模型拓扑结构包括输入层(input)、隐层(hidden layer)和输出层(output layer)。

BP网络可以学习和存贮大量的“输入-输出”模式映射关系，而无须事前了解描述这种映射关系是如何运作的。其学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

1.2.2L-M神经网络模型及贝叶斯优化算法。L-M优化算法(Train lm)相比传统BP神经网络模型，收敛速度明显较快，而且能得到很小的训练误差。贝叶斯优化算法的主要思想是利用已有的先验知识和数据对模型进行评价，先验知识利用与否是贝叶斯统计和经典统计之间的主要差别。传统BP神经网络模型的复杂度取决于训练样本的数量及其噪声的含量和映射函数的复杂度，模型过于复杂往往会导致学习效率下降、拟合效果不佳等问题，贝叶斯方法则可以提供了一套解决上述问题的方法，主要通过对控制模型复杂度的超参数定义模糊且非信息的先验概率来实现，最终的模型结果是所有模型以各自后验概率为权重的平均[3]。

1.2.3神经网络模型设计。

1.2.3.1节点级设计。神经元是神经网络处理信息的基本单位，其主要参数是神经元节点采用的激活函数。由于该研究模型的基础采用了由 BP 神经元组成的 BP 神经网络，因此该研究所构建的基于 BP 神经网络预测模型的隐含层神经元激活函数使用了对数 Sigmoid 函数，输出层神经元激活函数使用线性函数。

1.2.3.2网络级设计。该研究所采用的是前向网络结构，即先将神经元按照输入层、隐含层、输出层进行分组，再将各组间的神经元进行连接。在具体网络构造过程中，需要注意的参数有网络的层数，输入层、隐含层、输出层的神经元节点数，及节点间的连接方式。

(1)神经网络的层数。由于该研究采用的是前向网络结构，故输入层和输出层都只有1层，因此只有隐含层的层数不可确定。隐含层的数目可以不止1层，一般来说，问题越复杂，隐含层的层数和神经节点数越多，但在具体应用的过程中需要结合实际情况通过试验确定。虽然前苏联数学家 Andrey Nikolaevich Kolmogorov 已在理论上证实，一个3层的 BP 神经网络可以拟合任意函数，但该研究采用3层的BP神经网络拟合的结果并不理想，在使用4层的BP神经网络模型拟合后效果较为理想。因此，该研究最终选取了含有2个隐含层的4层 BP 网络模型结构。

(2)输入层和输出层节点数。从理论上而言，输入层的节点数和输出层的节点数与神经网络的性能没有关系，因此可以仅从试验数据特征的角度对输入层和输出层的节点数进行讨论。该研究综合考虑分析了胶合板期货日度价格数据的变化规律后，最终选用输入节点数为14，输出节点数为5。

(3)隐含层节点数。这是非常重要的一个参数，它的确定直接影响到神经网络模型的计算能力和对目标函数的逼近能力。但关于隐含层节点数的确定，目前还没有成熟的理论进行指导，人们往往根据建模经验和试凑法来确定隐含层的节点数。该研究选取的隐含层节点数分别为12和5个。

该研究所采用的L-M算法的BP神经网络模型核心代码如下[4]：

net.trainFcn=‘trainlm’;

net.trainParam.epochs=1000;

net.trainParam.goal=1e-6;

net=init(net);

贝叶斯算法的BP神经网络模型核心代码如下：

net.trainFcn=‘trainbr’;

net.trainParam.epochs=1 000;

net.trainParam.goal=0.001;

net=init(net);

2 结果与分析

设计好模型后，将上文提及的数据带入模型进行学习，该研究采用Matlab自带的神经网络工具箱中的L-M算法和贝叶斯算法进行训练，由于神经网络模型学习结果具有不确定性，因此学习时间和重要性水平每次学习可能均不一致，为了更好地比较两种算法在拟合期货价格的速度和拟合效果，该研究采用每种算法10次拟合平均结果作为各算法的均值。

2种算法拟合10次结果的均值见表1。

表1 L-M算法和贝叶斯优化算法10次拟合平均结果

从表1可以看出，贝叶斯优化算法相对于L-M算法具有相对更快的优势，同样的数量运算量下，由于贝叶斯优化算法可以在达到预设的收敛情况下终止学习，因此可以更快地对输入变量进行学习。L-M算法和贝叶斯算法拟合结果分别见图1a和图1b。

从图1可以看出，2种算法下BP神经网络都体现了较高的拟合度。

将2014年09月18日～2014年11月05日的胶合板主力期货合约作为测试数据带入上述训练的BP神经网络中进行预测，L-M算法和贝叶斯算法预测结果分别见图2a和图2b。

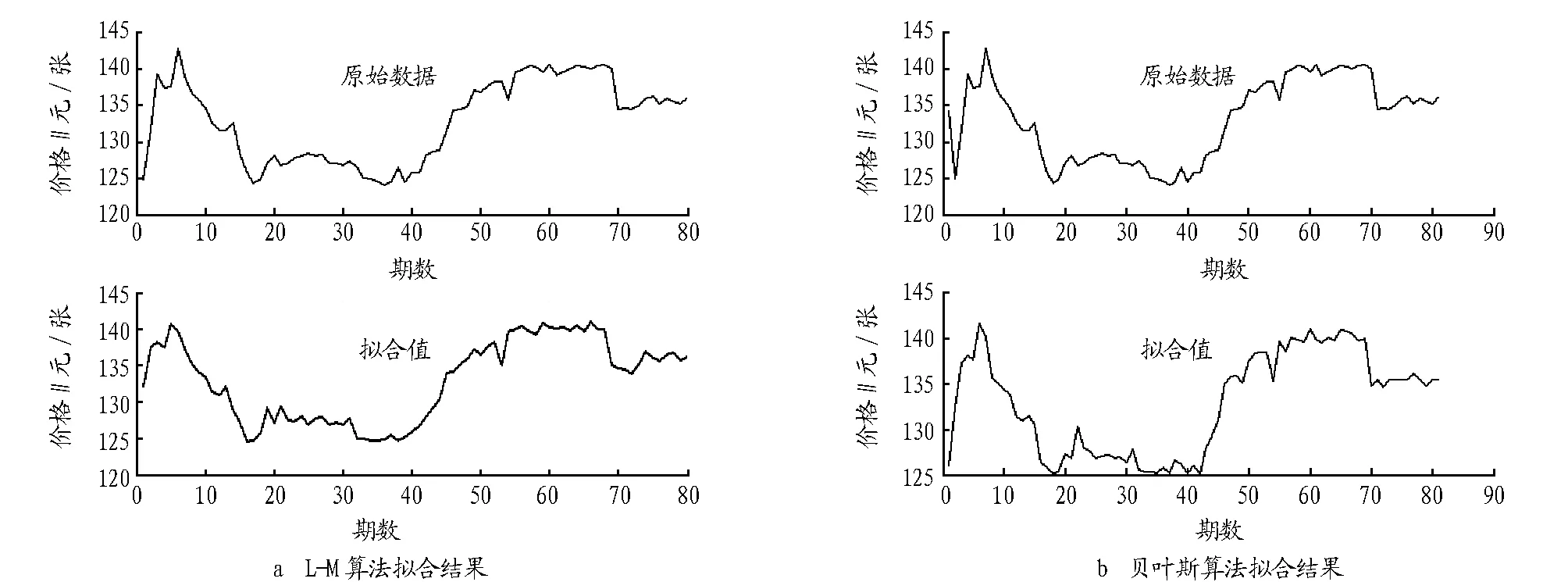
图1 基于BP神经网络模型的胶合板价格拟合结果

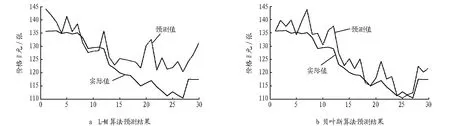
图2 基于BP神经网络模型的胶合板价格预测结果

由于BP神经网络模型学习过程具有较大的随机性，因此根据每次学习后得到的神经网络模型对原始数据进行预测得到的预测结果均不尽相同，图2所示预测结果并不代表贝叶斯算法的预测结果优于L-M算法。

从总体预测结果来看，2种算法得到的BP神经网络模型的预测值与实际值基本一致。因此，基于 BP 神经网络模型对期货价格进行预测具有一定的参考价值。但预测值和实际值具有较大的偏差，这是由于 BP 神经网络自身的问题所导致的。

综合两种算法的BP神经网络模型来看，贝叶斯算法相对L-M算法表现出了良好的效率性和相对更高的拟合优度。

3 结论与建议

该研究利用L-M算法的BP神经网络模型和贝叶斯算法的BP神经网络模型对大连商品交易所的胶合板期货合约价格进行了预测。结果表明，2种优化算法的BP神经网络模型均表现了较高的拟合速度和拟合精度，其中贝叶斯算法性能较优。该研究所述期货价格预测方法同样适用于其他类型期货价格预测，可为投资者投资决策提供参考。

[1] 中国期货业协会.期货投资分析[M].北京：中国财政经济出版社，2011.

[2] 王科明，杨建刚，周炜彤.利用人工神经网络技术预测期货行情[J].计算机工程与设计，2004，25(7):1164-1169.

[3] 王小平，曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社，2000:10-78.

[4] 禹建丽，孙增圻，VALERI KROUMOV，等.基于BP神经网络的股市建模与决策[J].系统工程理论与实践，2003(5):5-15.

Short-term Plywood Futures Prices Forecast Based on Two Neural Network Model

LIU Da-peng

(School of Economics and Management, Beijing Forestry University, Beijing100083)

This paper selects plywood main futures contract from December 06, 2013 to September 17, 2014 as training sample, plywood main futures contract September 18, 2014 to November 5, 2014 as the test data, using L-M optimization algorithms and Bayesian optimization algorithm BP neural network model to predict the futures price. The results show that the neural network model using two optimization algorithms are fitted with high degree of price movements have good predictive results, can provide reference for investors in the futures market.

Plywood futures; Prices predict; Neural network model

刘大鹏(1989-)，男，安徽凤阳人，硕士研究生，研究方向：区域经济学。

2015-03-26

S-9

A

0517-6611(2015)14-348-03