理想气体状态方程应用的难点突破
2015-01-19陈国钧
陈国钧
(南通科技职业学院,江苏 南通 226007)
气体状态方程是中学或普通物理教学中的重点和难点之一,公式表达形式虽然不复杂,但其用来解决的具体问题灵活性较大,且种类繁多。在教学中发现,很多学生对正确应用理想气体状态方程解题感到无所适从,不能举一反三,往往重复出现同样的错误。现在就如何突破这一教学难点,谈谈笔者的做法,以飨读者。
1 帮助学生建立应用气态方程解题的总体思路
思考物理问题,首先有一个正确分析问题的思路,善于捕捉共性特点,区分个性特点。因此,课堂上笔者在通过两道基本例题的分析后,引导学生归纳出应用气态方程解题的总体思路:
(1)了解物理过程,明确研究对象,注意研究对象有时不止一个,并分清热学研究对象和力学研究对象。
(2)确定同一研究对象的始末状态参量,对于多个研究对象的问题,应注意分别确定每个对象的始末态以及对应的参量,防止张冠李戴。
(3)列出气态方程求解,注意统一单位,尤其压强单位,温度要用热力学温标。
(4)解题时,注意相关条件和隐含条件,列出辅助方程。(5)善用整体思想分析问题。
2 通过对气体压强计算的单独处理,分散解题难点
学生解气态方程计算题时,错误率最高的就是不能将热学研究对象初末状态压强的表达式正确写出来。为了解决这个问题,采取将压强问题作为一个专题进行教学,以达到分散难点、突出重点,使学生在“强刺激”环境中突破难点。专题主要谈两个问题:一是压强单位如何统一,二是怎样确定压强表达式。具体如下:
2.1 压强单位如何统一
我们常见的压强单位有帕斯卡、大气压、厘米高水银柱等。一般学生对帕斯卡与大气压的互换,厘米高水银柱与帕的互换是不会感到困难的,有难度的是在牛顿第二定律表达式中怎样统一单位。
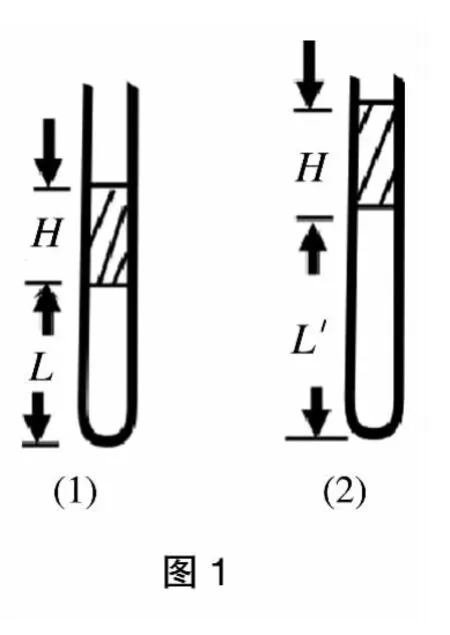
例1:在一个开口向上竖直放置的试管中,有一段长为H厘米的水银柱,下面封闭着长为L 的空气柱(如图1)。设外界大气压为P0,求试管以g/2 加速度下落时,空气柱长度变为多少?
此题在写末态气体压强时,由图1(2)对水银应用牛顿第二定律得:
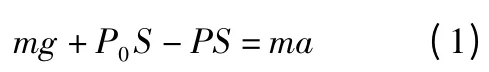
(1)式中P0、P 往往是cmHg为单位,如将cmHg 换算为帕比较麻烦。为此,我们可对(1)式进行恒等变换,总结出一般方法:将方程两边同除S 得
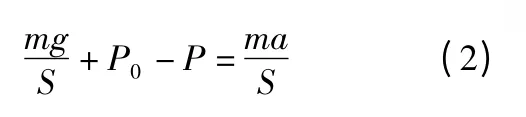

2.2 压强表达式的正确表述
综观气体压强的计算可分为两大类:一是被研究对象处于平衡状态,二是研究对象处在加速系统中。
2.2.1 被研究对象处在平衡系统中
在教学中,分别对液柱封闭气体、活塞封闭气体情况下的压强计算,通过例题分析归纳可得基本方法:在平衡系统中应对力学对象进行受力分析,不能忽视大气压,然后由平衡条件来求解。
对液柱封闭气体的压强求解是最常见的题型,它可采用同一形式的公式为液柱与外界接触一方的气压,h 表示水银柱的竖直高度。
求活塞封闭气体情况下的压强也是常见的题型,如:
例2:如图2 内壁光滑的气缸内放有气密性好的两活塞A、B,已知A、B 质量分别为mA、mB,横截面积为SA、SB,且A、B 之间用细线连接并封闭着一定质量的气体,在大气压强的作用下处于静止状态,则此时封闭气体压强应为多大?(设外界大气压强为P0)
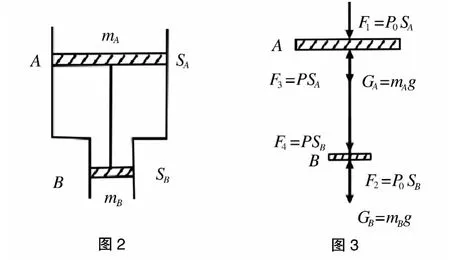
分析:该题属于力学研究对象处于平衡系统,故对活塞受力分析,如图3 所示。
由力学平衡条件得:P0SA+ mAg + mBg + PSB= P0SB+PSA
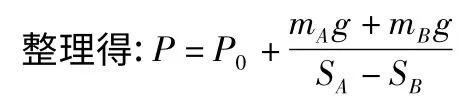
2.2.2 被研究对象处在加速系统中
此类问题在上述平衡系统中拓宽一下就可得求解路子:对力学对象进行受力分析后,用牛顿第二定律来求解即可。
例3:一端封闭的玻璃管,在封闭端有被长10cm 的水银柱封闭着的空气柱,当此玻璃管从斜面上滑下时,空气柱的压强多大?如图4 所示。(已知大气压强P 为75cmHg,玻璃管与斜面间的摩擦系数。
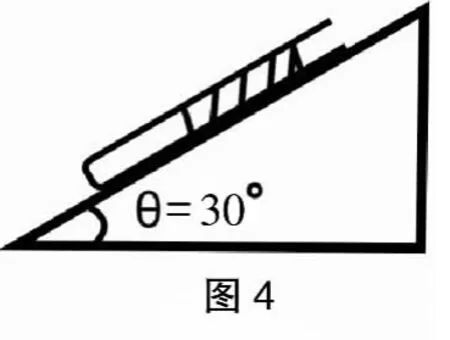
分析:对水银受力分析,受力图如图5 所示,由牛顿第二定律得:)
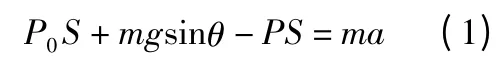
又将水银和试管作为整体由牛顿第二定律得:

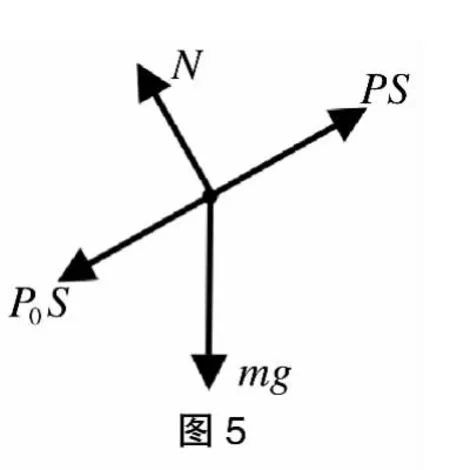
忽略试管质量,解(1)和(2)得:
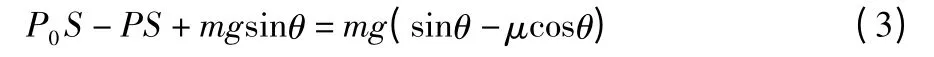
如压强单位为cmHg,则由压强单位换算方法可将(3)式写为:
3 对题型作系统分类,找出每类的共同特征,明确解题方法
学生对气态方程习题往往感到多而杂,心中一本糊涂账。因此,在教学中注重题型分类,帮助学生找出对应的解题方法,能起到事半功倍的效果。笔者将题型分为:单个热学研究对象、气体连接体问题、变质量问题、气体定律与能的转化和守恒定律的综合应用等四个方面。
3.1 单个热学研究对象
所谓单个热学研究对象,就是气体系统只有一个,这种题型的问题是最基本的,但不一定简单。关键是压强计算,而这一点我们已通过专题解决了。所以这类问题在这里便不难了。典型模型有水银柱、弹簧管、活塞问题。
如涉及到临界状态,则可先求出恰在临界状态的情况下的有关物理量,再与实际情况进行比较而得出气体所处的状态,再根据状态方程求解。
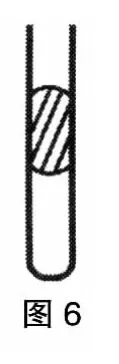
例4:如图6 所示,一端封闭的玻璃管长1m,内贮空气,气柱上面有一段高h=20cm 的水银柱,将空气封住,空气柱长49cm。若将玻璃管倒转至管口竖直向下,如果大气压等于76cmHg,求此时空气柱长度(全过程中温度不变)。
此题中试管倒过来,管中水银可能掉下来,也可能水银不掉下来。这就要先求一下水银恰不掉下时试管长度,然后将这个长度与实际长度比较一下,就不难得出结论。
3.2 气体连接体问题
所谓气体连接体问题,就是由两个(或两个以上)气体组成的系统。它们之间不是弧立的,而是有联系的。解此类问题的一般思路是:(1)隔离法逐个研究热学对象;(2)确定力学对象,写出压强表达式;(3)建立辅助方程。从三个方面着手:一是几何约束关系(体积),二是热学的联系(温度),三是力学约束关系(压强)。最后综合联立方程求解。
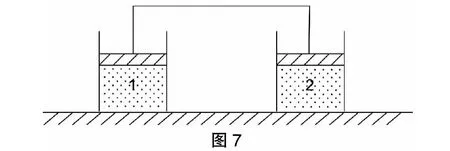
例5:两个相同的气缸活塞,用刚性连杆连接着,如图7所示。当温度为T 时,在这两个气缸内充以质量相等的空气,之后把其中一个气缸加热到T1,而另一气缸保持原来温度T 不变。若不计活塞和连杆的重力,大气压为P0,求气缸中的压强分别为多少?
分析:首先分别对1 和2 气体写出状态方程

然后找出约束方程分别为
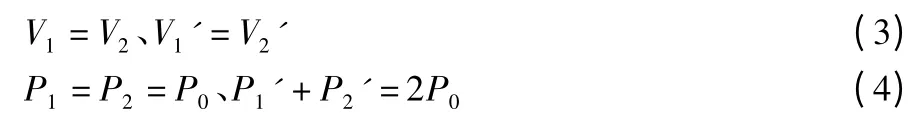
综合(1)(2)(3)(4)就可解得结果。
3.3 变质量问题
所谓变质量问题,就是各个气体系统在状态变化过程中,质量发生宏观迁移而重新分布,对每个气体研究对象来说都是变质量系统。此类问题一般方法有二种:一是克拉珀龙方程或道尔顿分压原理,二是虚拟法或无形弹性袋模型法。但第一种方法教材未涉及,故我们宜采用虚拟法,培养学生的空间形象思维能力。其方法:通过对整个状态过程的分析,虚拟一些简单的物理过程及状态参量,化变质量为不变质量,达到能运用气态方程的目的。
例6:某地与外界相通的教室,室温从27℃升高到42℃的过程中,剩余气体的质量占原来室内气体质量的百分比多大?
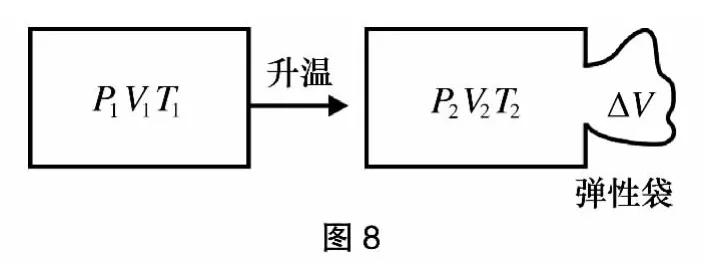
此问题可虚拟一个“无形”弹性袋将漏出气体全部收集起来,并利用此气袋的容积变化,将袋中气体变成与最终气体同温同压,如图8。这样以原来全部气体为研究对象,就不难求出所求量。
3.4 气体定律与能的转化和守恒定律的综合应用
气体的状态变化一般会伴随能量的变化,因此,气体状态变化过程中除了受到气体定律制约,还必须遵循能的转化和守恒定律。像这样有关气体定律与能的转化和守恒定律的综合题,其一般思路是:确定状态变化过程的特征,由温度变化判断内能的变化,由体积变化判定做功情况,列出能的转化方程,最后与气态方程联立求解。
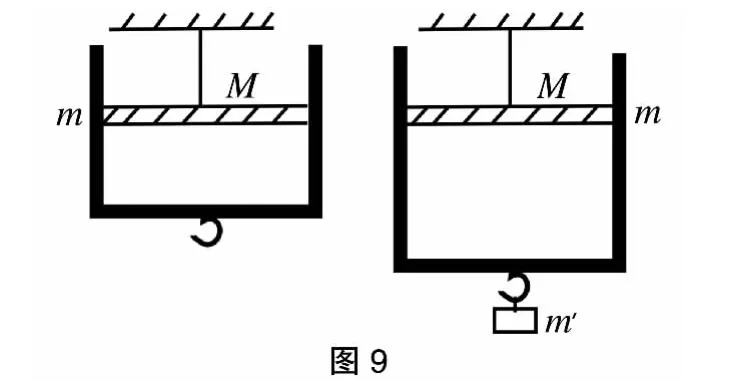
例7:如图9,质量为m=2kg 的气缸中有一截面积为S=10cm2的可在气缸内无摩擦移动的活塞,活塞的质量M=3kg,一根绳子系住活塞,将活塞和气缸一起吊起来处于平衡状态,这里活塞与气缸底相距h=10cm,大气压强为105Pa,取g=10 m/S2,当在汽缸下面的钩子上挂m' =3kg 重物后,气缸与重物组成的系统重新达到平衡位置时的动能为0.76焦。求这一过程中气缸内气体做功W汽是多少?设气缸的底面积等于活塞的面积,实验过程中温度保持不变。
分析:此题中的封闭气体作等温变化,气体膨胀对外做功,将气缸与重物组成的系统作为力学研究对象,由动能定理得:
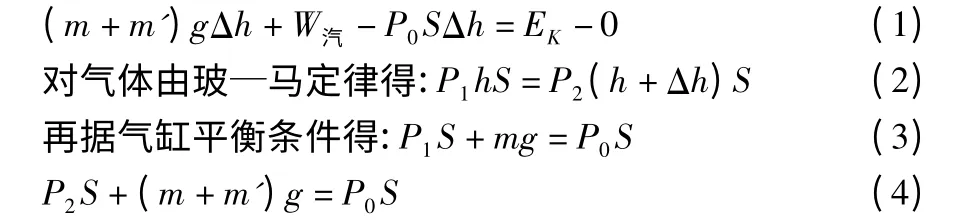
解(2)(3)(4)可得Δh=0.06m,代入(1)式可得气体做功W汽=3.76焦。
教学实践表明,通过以上教学过程的处理,能收到比较好的教学效果。
[1]聂品.理想气体状态方程的导出公式及其应用[J].曲阜师院学报:自然科学版,1981,(3) :54—57.
[2]孙海祥.气体状态方程四种表达式的讨论[J].重庆师范学院学报:自然科学版,1996,(13) :119—121.
[3]王生贵.理想气体状态方程教学中的若干问题[J].九江师专学报:自然科学版,1991,(6) :73—76.
[4]刘卫兴.略论理想气体状态方程的应用[J].宁德师专学报:自然科学版,2004,(4) :413—416.
[5]孙海祥. 理想气体状态方程综述[J]. 冀东学刊,1995,(5) :15—16.
