例析均值不等式工具性视角下的解题技巧
2015-01-19王莉敏
新课程(中学) 2015年10期
王莉敏
(江西省信丰中学)
均值不等式作为一种解题工具,它在许多问题的解决中应用得较为广泛,而且表现出独特的功能.然而,在使用均值不等式解决问题时,通常需要配合一定的变形与转化技巧,既有难度又不失灵活性.现举例说明如下:
一、凑项
例1.若0<x<1,求函数y=x4(1-x2)的最大值.
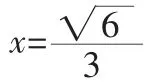
二、配项
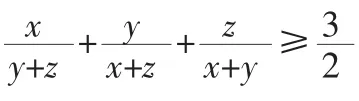
证明:要证原不等式成立,
三、拆项
例3.已知a1,a2,…,an∈R+且a1·a2…an=1,求证:(2+a1)(2+a2)…(2+an)≥3n.
当且仅当a1=a2=…=an=1 时等号成立.所以原命题得证.
四、串求
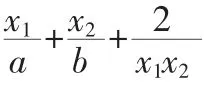
时
五、换元
例5.已知a,b,c 为△ABC 三边的长,求证:abc≥(a+b-c)(b+c-a)(c+a-b).
证明:设m=b+c-a,n=c+a-b,p=a+b-c,
即abc≥(a+b-c)(b+c-a)(c+a-b).
六、待定系数
例6.已知0<x<1,求y=x-x3的最大值.
解:因为0<x<1,所以1-x=0,又因为y=x-x3=x(1-x)(1+x)
