普通空间矢量法在级联多电平载波调制中的应用

董 寒，席自强，俞晨光

（湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉430068）

载波脉宽调制（sine pulse width modulation，SPWM）控制方法和空间矢量脉宽调制（space vector pulse width modulation，SVPWM）控制方法是目前两电平和多电平换流器控制系统中常用的两种脉宽调制技术。在级联多电平中，载波脉宽调制主要包括阶梯波宽度调制法（Step Modulation PWM）、载波移相SPWM 法（CPS-SPWM）和载波层叠法（Carrier Disposition PWM）；而空间矢量脉宽调制在多电平换流器中当电平数超过5时算法过于复杂，因此广泛应用于两电平或三电平的换流器的脉宽调制，由于该方式具有电压利用率高、谐波含量低及开关损耗小等优点而受到广泛的关注和应用，期望能将其所具有的优点运用到级联多电平中。本文在分析了两电平SVPWM的基本原理及其与载波调制的联系的基础上，将演变出的不连续调制方式应用到级联H桥多电平载波相移PWM（CPSSPWM）中，实现级联多电平变换器开关损耗的减少和谐波畸变等的优化，并通过Matlab软件的Simulink模块进行仿真验证。

1 两电平SVPWM调制方法与载波调制的联系

在SPWM中，通过模拟电路使调制波和三角载波比较实现PWM输出的方法为自然采样法，另一种更适合微处理器在软件中实现的方法为规则采样法。规则采样法的基本原理见图1。图1中Ts为采样周期，ur为正弦调制波，uc为三角载波，由于三角载波频率远大于正弦调制波频率，因此在一个采样周期中，正弦调制波可以等效为一个恒定值，即可以用AB对应的脉宽来代替CD，避免大量的计算，输出脉冲在ur＞uc时为高电平Ton。

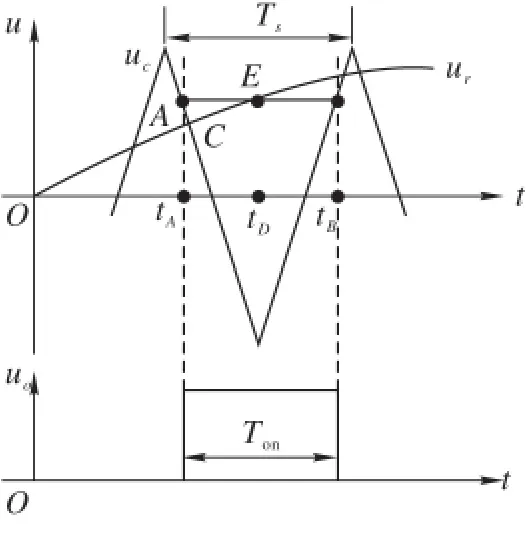
图1 对称规则采样法原理

设定三角载波幅值uc为1，调制比m＝ur/uc，可得正弦调制信号

根据图1中的几何关系可得输出的脉宽Ton大小为

结合式（1）、（2）中调制波与输出脉宽宽度的关系式可得到调制波表达式和对应脉宽之间的关系式

在载波调制的规则采样法中载波和调制波的意义很清楚，而空间矢量脉宽调制中则无明显的调制波定义，图2为电压空间矢量调制原理图，8种开关状态对应8个基本空间电压矢量V0～V7，其中V0和V7为零矢量，其余6个电压矢量为非零矢量，并按逆时针方向依次滞后60°，6个非零矢量将平面空间划分为6个60°的扇区Ⅰ～Ⅵ。

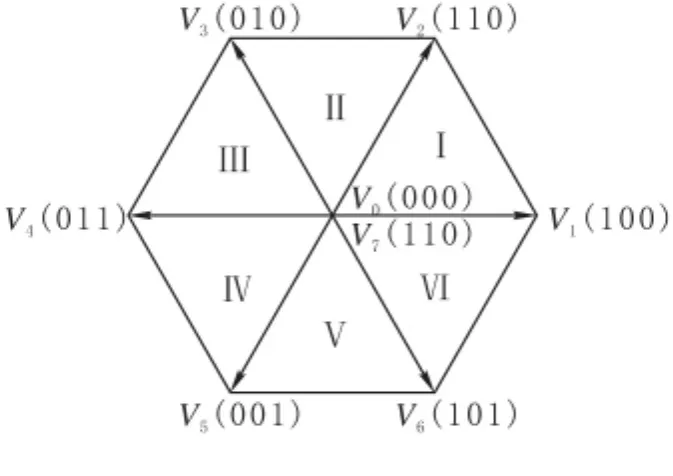
图2 两电平空间矢量图

以扇区Ⅰ为例，对应图1规则采样原理，分析两者之间的联系可以得到式（4）［3］，其中T00、T07分别为图2中V0、V7这两个零矢量的作用时间

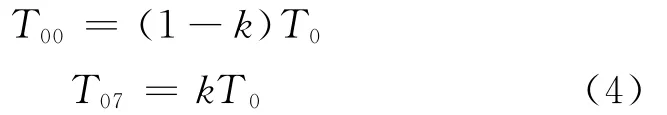
结合式（3）得到压空间矢量脉宽调制在整个360°范围内的三相电压调制波统一表达式为

式中k 的范围为0～1，VA＊、VB＊、VC＊分别为SVPWM调制中对应调制波数据，由式（5）可知SVPWM调制也可理解为在正弦调制波基波中加入零序分量Vz的规则采样SPWM，其中零序分量Vz的表达式随着k值的变化而变化，不同的k值对应向正弦调制波基波中注入不同的零序分量，从而产生不同的调制波。从中可以看出SVPWM法和载波SPWM法之间的联系。但这种联系是建立在两电平中的，本文通过分析和仿真将这种方法应用到级联多电平载波调制中，能得到和在两电平中相似的结果，并验证之。

2 空间矢量调制在级联多电平载波调制中的应用及Matlab仿真结果

2.1 级联H桥多电平变换器载波相移PWM调制

级联多电平变换器是由若干个基本变换单元串并联组合而成，基本单元有H桥、两电平和三电平换流器等。每个单元可输出方波或阶梯波并通过输出波形的叠加，形成更多电平的阶梯波以此逼近正弦电压或电流。本文是以一个三相8链节H桥换流器为仿真模型来分析SVPWM在级联多电平载波PWM中的应用，图3即为三相8链节H桥换流器的主电路图，其中载波调制方法采用的是载波相移法。

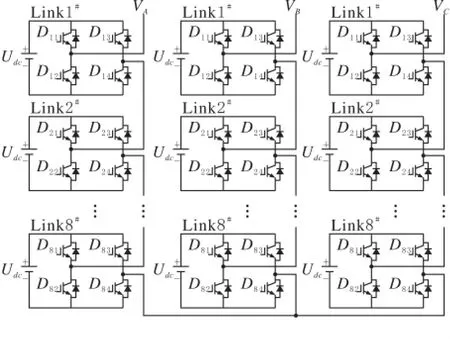
图3 三相级联8链节变流器主电路结构图

图3 所示每相包括了8个串联的H桥，三相H桥通过星型连接方式并联起来，VA、VB、VC分别为每相输出电压，Udc为每个桥臂直流侧电压，在仿真中设定Udc为1 000V，因此每相总直流侧电压为8 000V，若调制比m设为1，则输出线电压基波幅值为×8000V＝13.856kV。

对于该级联H桥变换器的仿真采用的调制方式为三角载波相移SPWM法。该方法是一种专门用于级联变换器的PWM方法，其基本原理是，每个变换器单元的调制信号均由一个三角载波和一个正弦调制波比较产生，比较原则与图1中规则采样法一致。对于n链节级联H桥，有n个变换器单元，故调制方法为n个互差π/n个相位的三角载波与同一个正弦调制波进行比较，分别输出这n个变换器的调制信号去驱动这n个单元开关管动作。图4为三相8链节H桥载波移相输出相电压的仿真波形。

通过在两电平SVPWM中分析得出使开关损耗降低的一种不连续调制方法，用Matlab仿真验证其在级联多电平载波SPWM中运用实现。

图4 A相相电压输出波形

通过在两电平SVPWM中分析得出使开关损耗降低的一种不连续调制方法，用Matlab仿真验证其在级联多电平载波SPWM中运用实现。

2.2 基于空间矢量的不连续调制方法

不连续调制方式是将相邻的半个载波周期中的有效空间矢量彼此移动到一起，二者之间的零空间矢量就随之消失了［1］。在普通两电平PWM调制中，从三角载波PWM的概念来说，这种不连续调制方式使每一相的调制波至少有一段等于正的或负的三角载波峰值，因此这段时间内该相的开关器件无开关动作，从而减小开关损耗。从SVPWM的概念来说，通过对式（4）和式（5）的分析，可知改变k的值可以改变两个零矢量的放置方式，要消除零空间矢量，则k值被分配为1或0。当k＝0时对应零矢量V7不作用，仅V0作用，反之当k＝1时仅V7作用。

然而这种简单的只消除某一个零空间矢量的调制策略会出现上管一直导通下管一直关断或相反的情况，因此会造成一个桥臂上下两个开关管的导通损耗不相同，从而导致开关器件的热稳定性的不一致，最终造成系统的热不平衡，不利于系统的器件选型设计和长期稳定运行。

基于以上考虑，提出一种内在的能平衡开关损耗的改进的不连续调制策略被提出［3］，即在基波周期中相继的60°扇区上交替地消除零空间矢量V0和V7。结合式（4）、（5），即交替地让k值取1和0，即k为一个幅值为1，占空比为0.5的方波。

由该调制策略可得出两种不同的k值切换方式:一种是在不同的扇区让k交替为1和0，得到正负半波各60°不动作的PWM波形，但波形的对称性较差；另一种方式是在扇区中点进行k值的切换，并可以得到对称的调制波，因此本文的仿真采用的是在扇区中点进行k值的切换，并将这种不连续调制方式应用到图3所示的三相级联8链节H桥变换器中，观察其输出相电压并分析是否有开关损耗的减小。前面所述的第二种k值切换方式又分两种情况，第一种情况是在－30°～30°区域内，即在一个周波的后30°和下一个周波的前30°区域内k值设定为1，然后每隔60°的相位k值切换一次，即在每个扇区的中点进行k值的切换，其仿真得到的调制波和零序分量如图5a所示，图5b为对应8链节级联H桥每相相电压输出波形；第二种情况则是相反的情况，在－30°～30°区域内k值设定为0，切换规则和第一种情况一致。

图5为在扇区中点进行k值切换的不连续调制方法在级联H桥多电平变换器中的应用的仿真波形，三相8链节级联H桥变换器输出电平数为2n＋1＝17（n＝8），图5b所示的相电压输出波形也可以反映出电平数，电平数越多，输出相电压波形越能逼近于调制波波形，使得谐波含量减小。从图中可以看出，最后总的输出相电压波形在每半个周期各有60°不动作区域，并关于一个周波的中点对称，输出相电压波形在这半个周波中各有30°区域为正的直流侧电压值8 000V和负的直流侧电压值－8 000V，解决了之前介绍的调制方式所引起的开关管的导通损耗不同所带来的问题。

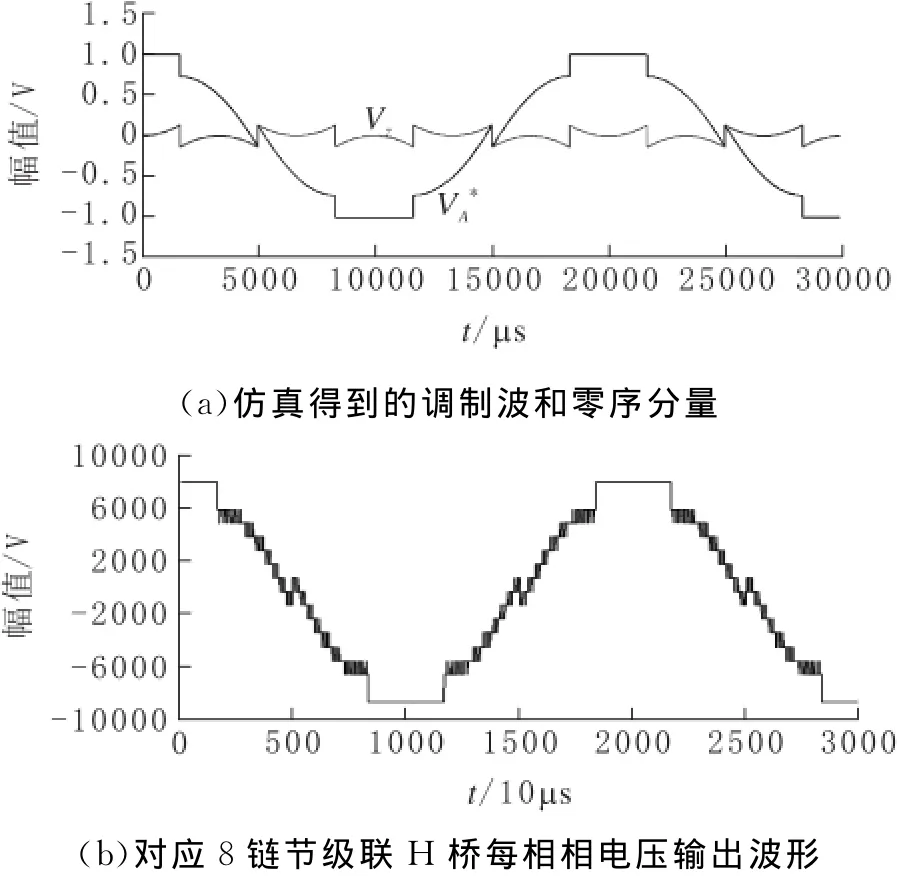
图5 k值在扇区中点切换时的调制波、零序分量和输出相电压

上述的分析和仿真将两电平SVPWM法中改变零矢量的放置位置与级联多电平中三角载波SPWM法结合起来，将该方法等效于向载波调制的调制波基波中注入某种零序分量产生不同的调制波，演变出不同的调制方式，实现不同的优化功能，并将其应用于级联H桥多电平变换器中。

2.3 仿真结果及分析

重点分析了基于空间矢量的不连续调制方式在级联多电平中的应用，在不改变开关频率和直流侧电压的情况下减小开关损耗。仿真结果显示输出相电压波形和生成的调制波波形保持一致，达到开关管不动作的要求。由于注入的零序分量的频率为基波频率的3倍，即为3次谐波，在三相输出的线电压中每相的3次谐波就被抵消掉了，因此不同的k值切换方式得到不同的调制波，但最后得到的线电压的波形和谐波畸变率差别不大。图6～8分别为普通载波相移SPWM调制的输出线电压仿真波形和谐波畸变率，及对应图5中k值切换方式和对应的另一种方式下不连续调制的输出线电压仿真波形和谐波畸变率。

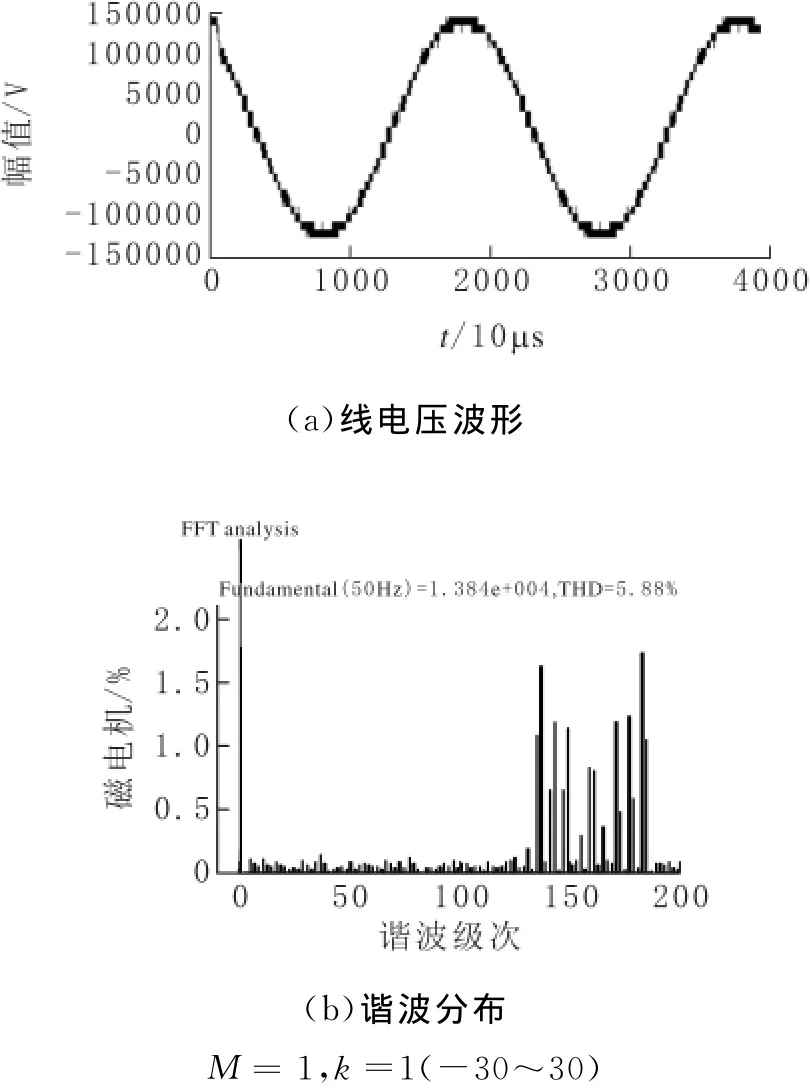
图6 普通载波相移SPWM调制输出线电压波形和谐波分布

图7 k＝1（－30°～30°）调制输出线电压波形和谐波分布

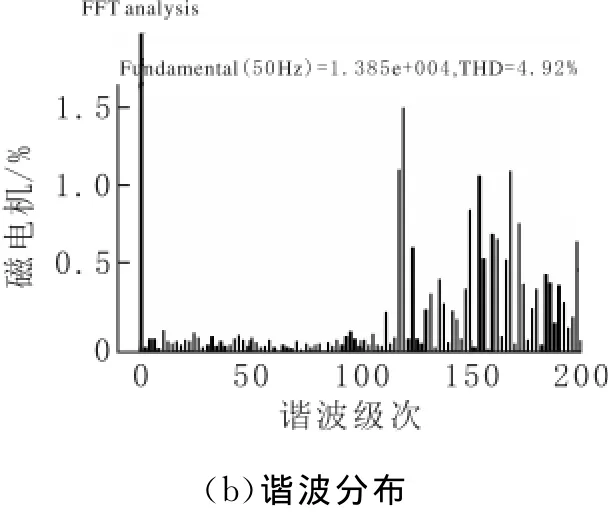
图8 k＝0（－30°～30°）调制输出线电压波形和谐波分布

根据以上仿真结果可知，两种不同情况下的扇区中点k值切换调制方式下输出的线电压，无论是从基波幅值还是波形都和未加入零序分量的载波相移调制无明显差别，这也验证了注入的零序分量频率为基频的3倍，在输出的线电压中被抵消掉了，故对输出的线电压波形和幅值无影响。并且图6～8中的谐波分布也可以验证，这种k值扇区中点切换的不连续调制方式使谐波畸变情况变好，两种情况下的谐波畸变率为5.01%和4.92%，在普通的载波相移调制下的谐波畸变5.88%，有明显的改善，使得THD值保持在5%以内。通过仿真可以知道，在两电平SVPWM中得到的不连续调制方式也可以在级联多电平的变换器中应用，并且可以得到与在两电平中相似的结论。

3 结论

文章根据在两电平中SVPWM和PWM之间的联系，将一种不连续调制方式应用到级联8链节H桥（17电平）变换器中，将不同条件下的不连续调制通过Matlab/Simulink仿真。仿真结果表明，空间矢量调制中演变出的不连续调制方式在级联多电平调制中仍然适用，并且可以得到与在两电平中相似的结论，即能使开关损耗降低并减小谐波畸变，而最终输出的线电压波形和幅值不受影响。

［1］ D.Grahame Holmes，Thomas A Lipo.Pulse width modulation for power converters:principles and practice［M］.America:Wiley-IEEE Press，2003.

［2］ 陈 娟，何英杰，王新宇，等.三电平空间矢量与载波调制策略统一理论的研究［J］.中国电机工程学报，2013，33（09）:71-78.

［3］ 王立乔，齐 飞.级联型多电平变流器新型载波相移SPWM 研究［J］.中国电机工程学报，2010（03）:28-34.

［4］ 屠卿瑞，徐 政，管敏渊，等.模块化多电平换流器环流抑制控制器设计［J］.电力系统自动化，2010（18）:57-61，83.

［5］ 吴洪洋，何湘宁.多电平载波PWM法与SVPWM法之间的本质联系及其应用［J］.中国电机工程学报，2002，22（05）:10-15.

［6］ 姜卫东，王群京，陈权，等.一种完全基于两电平空间矢量调制的三电平空间矢量调制算法［J］.电工技术学报，2009（01）:108-114.

［7］ 周卫平，吴正国，唐劲松，等.SVPWM的等效算法及SVPWM与SPWM的本质联系［J］.中国电机工程学报，2006（02）:133-137.

［8］ Iqbal A，Moinuddin S.Comprehensive relationship between carrier-based PWM and space vector PWM in a five-phase VSI［J］.IEEE Trans.on Power Electronics，2009，24（10）:2 379-2 390.